| Revision as of 22:27, 20 December 2005 edit208.255.152.227 (talk) →Superposition and Length Contraction← Previous edit | Revision as of 09:47, 26 December 2005 edit undoOrphanBot (talk | contribs)654,820 edits Removing image with no source information. Such images that are older than seven days may be deleted at any time.Next edit → | ||
| Line 55: | Line 55: | ||
| The non-trivial case involves one observer, say <math>S^\prime</math>, moving with a speed <math>v</math> in relation to <math>S</math> (and vice versa through symmetry). The resulting superposition has the axes of <math>S^\prime</math> tilted such that the slope of the time axis is <math>v/c</math> and the slope of the space axis is <math>c/v</math> (the slopes are with respect to the <math>t</math> axis). The light lines themselves become equivalent in the superposition. | The non-trivial case involves one observer, say <math>S^\prime</math>, moving with a speed <math>v</math> in relation to <math>S</math> (and vice versa through symmetry). The resulting superposition has the axes of <math>S^\prime</math> tilted such that the slope of the time axis is <math>v/c</math> and the slope of the space axis is <math>c/v</math> (the slopes are with respect to the <math>t</math> axis). The light lines themselves become equivalent in the superposition. | ||
| <div> | <div> | ||
| ] | <!-- Unsourced image removed: ] --> | ||
| </div> | </div> | ||
Revision as of 09:47, 26 December 2005
The Minkowski diagram is a graphical tool used in special relativity to visualize spacetime with regard to an inertial reference frame. They are also referred to as "spacetime diagrams".
Basic Minkowski Diagram
A Minkowski diagram is a representation of Minkowski space in an inertial reference frame. The simplest Minkowski diagram involves two dimensions, a time dimension and one space dimension. The time dimension is drawn vertically while the space dimension is drawn horizontally. Additionally, the scales of the axes can be adjusted such that a photon () passing through the origin describes a line of slope 1, or rather (the slope is with respect to the time axis). c is the observer invariant speed, or the speed of light.
Alternative Forms of the Minkowski Diagram
At times the time (y-) axis will be labelled ct. Do not let this confuse you. The y-axis is always time. The use of ct is introduced to uniform the dimensions of both axes to dimensions of length only. This has applications to the derivation of the slope described above. Given that c is an invariant, fundamental constant, it is one and the same for all frames of reference. Therefore, in equal times, the photon will travel equal distances - this equates to equal displacements in both the x- and y-axes. Using simple trigonometry it is possible to show that the angle subtended by the world-line of the light subtends an angle of 45° to both axes.
The Light Cone
Extending the Minkowski diagram to include a second space dimension then rotating the light path around the time axis creates a light cone.
This is effectively our world-line. We have only been affected by what we have seen in the past; this has brought us to where we are now - the origin. We will only be affected by what we see. Hence our future is described as well. The events that happen outside of the cone cannot be experienced.
This arises from a consideration of c. Since c is the fastest speed attainable, then all events must occur at speeds strictly less than c. Graphically, this is enclosed between the 45° lines in both spatial frames - hence the hour-glass shape.
Examples of Minkowski Diagrams
The Twin Paradox
See the twin paradox.
File:Twins paradox diagram.png
Hyperbolic Motion: The Uniformly Accelerating Object
See hyperbolic motion.
Superposition of Inertial Reference Frames
The superposition of inertial reference frames using a Minkowski diagram is an easy way to visualize the relationship of the two frames with regard to an event or a series of events.
Constructing the Minkowski Diagram
To begin, each observer, say and , constructs a Minkowski diagram with a single space dimension and time dimension with the observer at the origin. To differentiate the two sets of variables for each observer, observer uses and for the space and time dimensions while observer uses and .
The trivial case is when and occupy the same reference frame. This involves a direct superposition of one Minkowski diagram on top of the other.
Furthermore, if we synchronize the two sets of coordinates such that when one observer stands behind the other observer, as far as the other space dimensions are concerned, both observers set their clocks to zero, then the trivial case results in both coordinate systems being identical.
The non-trivial case involves one observer, say , moving with a speed in relation to (and vice versa through symmetry). The resulting superposition has the axes of tilted such that the slope of the time axis is and the slope of the space axis is (the slopes are with respect to the axis). The light lines themselves become equivalent in the superposition.
The Mechanics and Meaning of Superposition
Time Axis, or Time-like Lines
File:Timelike line S prime in S.png
A way to understand how the time axis of one coordinate system, , is superimposed on another coordinate system, , is to imagine the observer holding a flashing light source. In relation to the light source remains stationary as it flashes on and off. However in relation to the light source is in motion in the x-dimension. Graphing the events results in a tilted line in and a perfectly vertical line in . From this we can conclude that not only does the tilted line in represent the path, or worldline of but also the time axis of itself. Such a line is referred to as a time-like line.
Space Axis, or Space-like Lines
A way to understand how the space axis of one coordinate system, , is superimposed on another coordinate system, , is to imagine a series of light sources flashing simultaneously with respect to . Because of the relative nature of simultaneity, observes a series of flashing light sources going off in sequence one after the other. The result is a tilted line in and a perfectly horizontal line in . From this we can conclude that the tilted line in represents the line of simultaneity for which is its space axis. Such a line is referred to as a space-like line.
Superposition and the Lorentz Transformation
Superposition and Time Dilation
Superposition and Length Contraction
- Minkowski diagram showing relativistic length contraction.
Examination of a Minkowski diagram shows this effect is caused by a tilting relationship between two reference frames in space-time. The yellow area is a light cone. The black line are the space (x) and time (t) axis of observer in frame S. The blue line is the time axis (t') of frame S'. The purple line is the space axis (x') of a ship in frame S'. Note that in frame S', the light cone reaches both ends of the ship at the same time, while it doesn't in frame S. That is because when observer S is looking at both ends of the ship is looking a different points in the frame S' time lined. So the forward end of ship S' seen by observer S has not moved as far as the aft end, this results in ship S' being foreshortened to observer S.
The easiest way of imagining this, is to look at the Lorentz equations themselves. If a rigid set of points B1 and B2 are observed from a rigid set of points A1 and A2 to be moving along the (x) axis with velocity (v), the (x)coordinates of B1 and B2 at a time (t) would be described through x' = (x - vt)/(γ). This means that the distance between them undergoes a contraction by γ = in the A-coordinate system.
Conversely, points A1 and A2, when observed from B, will have a velocity (-v) along the x-axis. This does not affect the scaling factor (γ) which is a function of rather than v, which means that the distance A1-A2 also appears to contract by gamma. The properties of Minkowski space-time geometry can be succinctly put as 'the grass is shorter in the other side'.
Superposition and Tachyons
Tachyons are theoretical particles with speeds greater than . The path described by a tachyon corresponds to a space-like line. Drawing the path of a tachyon in a Minkowski diagram results in the conclusion that tachyons travel forwards or backwards in time depending on the observer.
Furthermore, drawing the path of a tachyon in a Minkowski diagram results in the conclusion that tachyons also travel at infinite speed, depending on the observer.
References
| This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Spacetime diagram" – news · newspapers · books · scholar · JSTOR (Learn how and when to remove this message) |

 ) passing through the origin describes a line of slope 1, or rather
) passing through the origin describes a line of slope 1, or rather  (the slope is with respect to the time axis). c is the observer
(the slope is with respect to the time axis). c is the observer  and
and  , constructs a Minkowski diagram with a single space dimension and time dimension with the observer at the origin. To differentiate the two sets of variables for each observer, observer
, constructs a Minkowski diagram with a single space dimension and time dimension with the observer at the origin. To differentiate the two sets of variables for each observer, observer  and
and  for the space and time dimensions while observer
for the space and time dimensions while observer  and
and  .
.


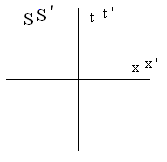
 in relation to
in relation to  and the slope of the space axis is
and the slope of the space axis is  (the slopes are with respect to the
(the slopes are with respect to the 
 in the A-coordinate system.
in the A-coordinate system.
 rather than v, which means that the distance A1-A2 also appears to contract by gamma. The properties of Minkowski space-time geometry can be succinctly put as 'the grass is shorter in the other side'.
rather than v, which means that the distance A1-A2 also appears to contract by gamma. The properties of Minkowski space-time geometry can be succinctly put as 'the grass is shorter in the other side'.
 . The path described by a tachyon
. The path described by a tachyon  corresponds to a space-like line. Drawing the path of a tachyon in a Minkowski diagram results in the conclusion that tachyons travel forwards or backwards in time depending on the observer.
corresponds to a space-like line. Drawing the path of a tachyon in a Minkowski diagram results in the conclusion that tachyons travel forwards or backwards in time depending on the observer.

