| Revision as of 08:56, 29 December 2005 editFrancis Schonken (talk | contribs)Extended confirmed users68,468 editsm I'm not interested in the still continuing edit warring, but please use the correct disambig sentence, and maybe have a look at talk:arabic numerals#New intro and page lay-out proposal← Previous edit | Revision as of 15:38, 29 December 2005 edit undoAstriolok (talk | contribs)119 edits revert to correct versionNext edit → | ||
| Line 1: | Line 1: | ||
| {{Otheruses2|Arabic numerals}} | {{Otheruses2|Arabic numerals}} | ||
| ⚫ | {{Table Numeral Systems}} | ||
| ''This article is about the Hindu-Arabic numeral symbols. For the Hindu-Arabic numeral system, see ]. | ''This article is about the Hindu-Arabic numeral symbols. For the Hindu-Arabic numeral system, see ]. | ||
| '''Hindu-Arabic numerals''' |
'''Hindu-Arabic numerals''' also known as '''Arabic Numerals''', ''']''', ''']''', and '''Western numerals''' are the most common set of ] used to represent ]s around the world. They are considered an important milestone in the development of ]. | ||
| ] | |||
| == Origins of the symbols == | |||
| <div class="boilerplate seealso"> | |||
| ⚫ | |||
| </div> | |||
| Hindu-Arabic numerals are commonly known as "Arabic numerals". The latter term is a ], since what are known in the ] as "Arabic numerals" trace their origin to ], where they made their gradual appearance from about the 3rd century BC. The numerals reached Europe, albeit after further evolution, through the ], hence the misnomer. The Arabs referred to these numerals as the "Indian numerals", أرقام هندية, ''arqam hindiyyah''. | |||
| ==The term "Arabic Numerals"== | |||
| The numerals drifted over time to the west of India and were mentioned in Syria in the 7th century. They were widely popularised throughout the emerging Arab empire that then stretched from India to Spain by the writings of ] and ] mathematicians such as ], ], and ]. The Arab mathematician (973-1048 AD) ] wrote | |||
| What are known in ] as "Arabic numerals" were neither invented nor widely used by the ]s. Instead, they were developed in ] by the ] around ]. However, because it was Arabs who transmitted this system to the West after the Hindu numerical system found its way to ], the numeral system became known as "Arabic". Arabs themselves call the numerals "Indian numerals," أرقام هندية, ''arqam hindiyyah'') and they use their own distinct set of Arabic symbols for numerals. | |||
| :''What we use for numerals is a selection of the best and most regular figures in India.'' | |||
| ⚫ | ]s in ] in the first century AD]] | ||
| ] | |||
| The most widely used term for the numerals in academic journals is therefore Hindu-Arabic numerals. | |||
| In Europe, the numerals were first mentioned in Spain, then mostly under Arab rule, in the Codex Vigilanus of 976. Their use was advocated by the ] mathematician ] in his famous work '']'' of 1202, who studied them in northeastern ]. The European acceptance of the numerals was accelerated by the invention of the ], and by the middle of the 16th century most of Europe had accepted them. | |||
| ⚫ | ]s in the first century AD]] | ||
| ==How the numerals were transmitted from India to Europe == | |||
| ⚫ | ==Description== | ||
| ⚫ | {{Table Numeral Systems}} | ||
| ] inscriptions from around 300 B.C. use the symbols which became 1, 4 and 6. One century later, their use of the symbols which became 2, 4, 6, 7 and 9 was recorded. | |||
| How the numbers came to the Arabs can be read in the work of al-Qifti's "Chronology of the scholars", which was written around the end the ] but quoted earlier sources : | |||
| ⚫ | |||
| :''... a person from India presented himself before the ] ] in the year ] who was well versed in the siddhanta method of calculation related to the movement of the heavenly bodies, and having ways of calculating equations based on the half-chord calculated in half-degrees ... Al-Mansur ordered this book to be translated into Arabic, and a work to be written, based on the translation, to give the Arabs a solid base for calculating the movements of the planets ...'' | |||
| This book, which the Indian scholar presented from, was probably ] (The Opening of the Universe) which was written in ] by the Indian mathematician ] and had used the Hindu Numerals with the zero sign. | |||
| ⚫ | The Arabic numeral system has used many different sets of symbols. These symbol sets can be divided into two main families — namely the West Arabic numerals, and the East Arabic numerals. East Arabic numerals — which were developed primarily in what is now ] — are shown in the table below as ''Arabic-Indic''. ''East Arabic-Indic'' is a variety of East Arabic numerals. West Arabic numerals — which were developed in ] and the ] —are shown in the table, labelled ''European''. (There are two ] styles for rendering European numerals, known as lining figures and ]). | ||
| The numeral system came to be known to both the ] mathematician ], whose book ''On the Calculation with Hindu Numerals'' written about ], and the ] mathematician ], who wrote four volumes, "On the Use of the Indian Numerals" (Ketab fi Isti'mal al-'Adad al-Hindi) about ], are principally responsible for the diffusion of the Indian system of numeration in the ] and the West . In the ], ]ern mathematicians extended the decimal numeral system to include fractions, as recorded in a treatise by ] mathematician ] in ]-]. | |||
| ] | |||
| The first mentions of the numerals in the West are found in the Codex Vigilanus of 976 . | |||
| The tenth century mathematician ] who became is regarded as the first great scholar to spread the use of Hindu-Arabic numerals in Europe. As a monk and later as ] taught the numerals to European scholars. | |||
| ], an ] mathematician who had studied in ] (]), ], promoted the Arabic numeral system in ] with his book '']'', which was published in ]. | |||
| :"When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians' nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it.." | |||
| The system did not come into wide use in Europe, however, until the invention of printing (See, for example, the printed in Ulm, and other examples in the ] in ], ].) | |||
| In the Arab World—until modern times—the Arabic numeral system was used only by mathematicians. Muslim scientists used the ], and merchants used a numeral system similar to the ] and the ]. Therefore, it was not until ] that the Arabic numeral system was used by a large population. | |||
| The European acceptance of the numerals was accelerated by the invention of the ], and by the middle of the sixteenth century most of Europe had accepted them. | |||
| ⚫ | ==Description== | ||
| ⚫ | Like many numbering systems, the numbers 1, 2, and 3 represent simple tally marks. 1 being a single line, 2 being two lines (now connected by a diagonal) and 3 being three lines (now connected by two vertical lines). After three, numbers tend to become more complex symbols (examples are the Chinese/Japanese numbers and ]). Theorists believe that this is because it becomes difficult to instantaneously count objects past three{{fact}}. | ||
| ⚫ | The Arabic numeral system has used many different sets of symbols. These symbol sets can be divided into two main families — namely the West Arabic numerals, and the East Arabic numerals. East Arabic numerals — which were developed primarily in what is now ] — are shown in the table below as ''Arabic-Indic''. ''East Arabic-Indic'' is a variety of East Arabic numerals. West Arabic numerals — which were developed in ] and the ] —are shown in the table, labelled ''European''. (There are two ] styles for rendering European numerals, known as lining figures and ]). | ||
| ==See also == | |||
| ⚫ | *] | ||
| ==References== | ==References== | ||
Revision as of 15:38, 29 December 2005
Template:Otheruses2 This article is about the Hindu-Arabic numeral symbols. For the Hindu-Arabic numeral system, see Hindu-Arabic numeral system.
Hindu-Arabic numerals also known as Arabic Numerals, Hindu numerals, European numerals, and Western numerals are the most common set of symbols used to represent numbers around the world. They are considered an important milestone in the development of mathematics.
The term "Arabic Numerals"
What are known in English as "Arabic numerals" were neither invented nor widely used by the Arabs. Instead, they were developed in India by the Hindus around 400 BC. However, because it was Arabs who transmitted this system to the West after the Hindu numerical system found its way to Persia, the numeral system became known as "Arabic". Arabs themselves call the numerals "Indian numerals," أرقام هندية, arqam hindiyyah) and they use their own distinct set of Arabic symbols for numerals.


The most widely used term for the numerals in academic journals is therefore Hindu-Arabic numerals.
How the numerals were transmitted from India to Europe
| Part of a series on | ||||
| Numeral systems | ||||
|---|---|---|---|---|
Place-value notation
|
||||
Sign-value notation
|
||||
| List of numeral systems | ||||
Buddhist inscriptions from around 300 B.C. use the symbols which became 1, 4 and 6. One century later, their use of the symbols which became 2, 4, 6, 7 and 9 was recorded.
How the numbers came to the Arabs can be read in the work of al-Qifti's "Chronology of the scholars", which was written around the end the 12th century but quoted earlier sources :
- ... a person from India presented himself before the Caliph al-Mansur in the year 776 who was well versed in the siddhanta method of calculation related to the movement of the heavenly bodies, and having ways of calculating equations based on the half-chord calculated in half-degrees ... Al-Mansur ordered this book to be translated into Arabic, and a work to be written, based on the translation, to give the Arabs a solid base for calculating the movements of the planets ...
This book, which the Indian scholar presented from, was probably Brahmasphutasiddhanta (The Opening of the Universe) which was written in 628 by the Indian mathematician Brahmagupta and had used the Hindu Numerals with the zero sign.
The numeral system came to be known to both the Persian mathematician Al-Khwarizmi, whose book On the Calculation with Hindu Numerals written about 825, and the Arab mathematician Al-Kindi, who wrote four volumes, "On the Use of the Indian Numerals" (Ketab fi Isti'mal al-'Adad al-Hindi) about 830, are principally responsible for the diffusion of the Indian system of numeration in the Middle-East and the West . In the 10th century, Middle-Eastern mathematicians extended the decimal numeral system to include fractions, as recorded in a treatise by Syrian mathematician Abu'l-Hasan al-Uqlidisi in 952-953.
The first mentions of the numerals in the West are found in the Codex Vigilanus of 976 .
The tenth century mathematician Gerbert of Aurillac who became is regarded as the first great scholar to spread the use of Hindu-Arabic numerals in Europe. As a monk and later as Pope Silvester II taught the numerals to European scholars.
Fibonacci, an Italian mathematician who had studied in Bejaia (Bougie), Algeria, promoted the Arabic numeral system in Europe with his book Liber Abaci, which was published in 1202.
- "When my father, who had been appointed by his country as public notary in the customs at Bugia acting for the Pisan merchants going there, was in charge, he summoned me to him while I was still a child, and having an eye to usefulness and future convenience, desired me to stay there and receive instruction in the school of accounting. There, when I had been introduced to the art of the Indians' nine symbols through remarkable teaching, knowledge of the art very soon pleased me above all else and I came to understand it.."
The system did not come into wide use in Europe, however, until the invention of printing (See, for example, the 1482 Ptolemaeus map of the world printed in Ulm, and other examples in the Gutenberg Museum in Mainz, Germany.)
In the Arab World—until modern times—the Arabic numeral system was used only by mathematicians. Muslim scientists used the Babylonian numeral system, and merchants used a numeral system similar to the Greek numeral system and the Hebrew numeral system. Therefore, it was not until Fibonacci that the Arabic numeral system was used by a large population.
The European acceptance of the numerals was accelerated by the invention of the printing press, and by the middle of the sixteenth century most of Europe had accepted them.
Description
Like many numbering systems, the numbers 1, 2, and 3 represent simple tally marks. 1 being a single line, 2 being two lines (now connected by a diagonal) and 3 being three lines (now connected by two vertical lines). After three, numbers tend to become more complex symbols (examples are the Chinese/Japanese numbers and Roman numerals). Theorists believe that this is because it becomes difficult to instantaneously count objects past three.
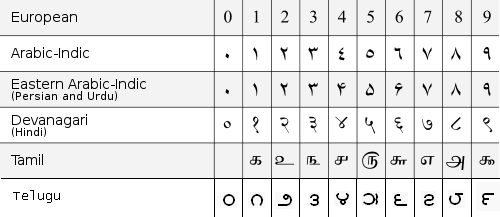
The Arabic numeral system has used many different sets of symbols. These symbol sets can be divided into two main families — namely the West Arabic numerals, and the East Arabic numerals. East Arabic numerals — which were developed primarily in what is now Iraq — are shown in the table below as Arabic-Indic. East Arabic-Indic is a variety of East Arabic numerals. West Arabic numerals — which were developed in al-Andalus and the Maghreb —are shown in the table, labelled European. (There are two typographic styles for rendering European numerals, known as lining figures and text figures).
See also
References
- History of Counting Systems and Numerals. Retrieved 11 December 2005.
- The Evolution of Numbers. 16 April 2005.
- O'Connor, J. J. and Robertson, E. F. Indian numerals. November 2000.
External links
- History of the Numerals