| Revision as of 23:30, 21 December 2009 editSothicus (talk | contribs)131 edits Undid revision 333147170 by 66.41.3.85 (talk)← Previous edit | Revision as of 22:13, 6 January 2010 edit undo134.117.196.101 (talk) →Cue SportsNext edit → | ||
| Line 36: | Line 36: | ||
| Using the ], |'''v<sub>1</sub>'''|<sup>2</sup> = '''v<sub>1</sub>•v<sub>1</sub>''' = |'''V<sub>1</sub>'''|<sup>2</sup>+|'''V<sub>2</sub>'''|<sup>2</sup>+2'''V<sub>1</sub>•V<sub>2</sub>''' | Using the ], |'''v<sub>1</sub>'''|<sup>2</sup> = '''v<sub>1</sub>•v<sub>1</sub>''' = |'''V<sub>1</sub>'''|<sup>2</sup>+|'''V<sub>2</sub>'''|<sup>2</sup>+2'''V<sub>1</sub>•V<sub>2</sub>''' | ||
| So '''V<sub>1</sub>•V<sub>2</sub>''' = 0, so they are perpendicular. | So '''V<sub>1</sub>•V<sub>2</sub>''' = 0, so they are perpendicular. <== wut? | ||
| ==Attack== | ==Attack== | ||
Revision as of 22:13, 6 January 2010
For other uses, see Collision (disambiguation).A collision is an isolated event in which two or more moving bodies (colliding bodies) exert relatively strong forces on each other for a relatively short time.
Dynamics
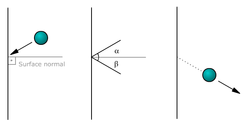
Collisions involve forces (there is a change in velocity). Collisions can be elastic, meaning they conserve energy and momentum, inelastic, meaning they conserve momentum but not energy, or totally inelastic (or plastic), meaning they conserve momentum and the two objects stick together.
The magnitude of the velocity difference at impact is called the closing speed.
The field of dynamics is concerned with moving and colliding objects.
Elastic and Inelastic Collisions
A perfectly elastic collision is defined as one in which there is no loss of kinetic energy in the collision. An inelastic collision is one in which part of the kinetic energy is changed to some other form of energy in the collision. Any macroscopic collision between objects will convert some of the kinetic energy into internal energy and other forms of energy, so no large scale impacts are perfectly elastic. Momentum is conserved in inelastic collisions, but one cannot track the kinetic energy through the collision since some of it is converted to other forms of energy. Collisions in ideal gases approach perfectly elastic collisions, as do scattering interactions of sub-atomic particles which are deflected by the electromagnetic force. Some large-scale interactions like the slingshot type gravitational interactions between satellites and planets are perfectly elastic. Collisions between hard spheres may be nearly elastic, so it is useful to calculate the limiting case of an elastic collision. The assumption of conservation of momentum as well as the conservation of kinetic energy makes possible the calculation of the final velocities in two-body collisions.
Mathematical description
Let the linear, angular and internal momenta of a molecule be given by the set of r variables { pi }. The state of a molecule may then be described by the range δwi = δp1δp2δp3 ... δpr. There are many such ranges corresponding to different states; a specific state may be denoted by the index i. Two molecules undergoing a collision can thus be denoted by (i, j) (Such an ordered pair is sometimes known as a constellation.)
It is convenient to suppose that two molecules exert a negligible effect on each other unless their centre of gravities approach within a critical distance b. A collision therefore begins when the respective centres of gravity arrive at this critical distance, and is completed when they again reach this critical distance on their way apart. Under this model, a collision is completely described by the matrix , which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision.
This notation is convenient in proving Boltzmann's H-theorem of statistical mechanics.
Cue Sports
| This section may require cleanup to meet Misplaced Pages's quality standards. No cleanup reason has been specified. Please help improve this section if you can. (February 2008) (Learn how and when to remove this message) |
In cue sports, collisions play an important role. Because the collisions between billiard balls are nearly elastic, and the balls roll on a surface that produces low-rolling friction, their behavior is often used to illustrate Newton's laws of motion. After a low-friction collision of a moving ball with a stationary one of equal mass, the angle between the directions of the two balls is 90 degrees. This appears to be an important fact that many professional billiard players take into account.
Consider an elastic collision in 2 dimensions of any 2 masses m1 and m2, with respective initial velocities v1 in the x-direction, and v2 = 0, and final velocities V1 and V2.
Conservation of momentum: m1v1 = m1V1+ m2V2.
Conservation of energy for elastic collision: (1/2)m1|v1| = (1/2)m1|V1| + (1/2)m2|V2|
Now consider the case m1 = m2, we then obtain v1=V1+V2 and |v1| = |V1|+|V2|
Using the dot product, |v1| = v1•v1 = |V1|+|V2|+2V1•V2
So V1•V2 = 0, so they are perpendicular. <== wut?
Attack
Types of attack by means of a deliberate collision include:
- with the body: unarmed striking, punching, kicking, martial arts, pugilism
- striking directly with a weapon, such as a sword, club or axe
- ramming with an object or vehicle, e.g.:
- a car deliberately crashing into a building to break into it
- a battering ram, medieval weapon used for breaking down large doors, also a modern version is used by police forces during raids
An attacking collision with a distant object can be achieved by throwing or launching a projectile.
Space exploration
An object may deliberately be made to crash-land on another celestial body, to do measurements and send them to Earth before being destroyed, or to allow instruments elsewhere to observe the effect. See e.g:
- During Apollo 13, Apollo 14, Apollo 15, Apollo 16 and Apollo 17, the S-IVB (the rocket's third stage) was crashed into the Moon in order to perform seismic measurement used for characterizing the lunar core.
- Deep Impact (space mission)
- SMART-1 - European Space Agency satellite
- Moon impact probe - ISRO probe
See also
- Coefficient of restitution
- Collision detection
- Collision (telecommunications)
- Car accident
- Elastic collision
- Friction
- Impact crater
- Impact event
- Inelastic collision
- Kinetic theory
- collisions between molecules - Mid-air collision
- Projectile
- Space debris
Notes
- Alciatore, David G. (January 2006). "TP 3.1 90° rule" (PDF). Retrieved 2008-03-08.
References
- Tolman, R. C. (1938). The Principles of Statistical Mechanics. Oxford: Clarendon Press. Reissued (1979) New York: Dover ISBN 0-486-63896-0.
External links
- Three Dimensional Collision - Oblique inelastic collision between two homogeneous spheres.
- Two Dimensional Collision - Java applet that simulates elastic collisions.
- One Dimensional Collision - One Dimensional Collision Flash Applet.
- Two Dimensional Collision - Two Dimensional Collision Flash Applet.
 , which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision.
, which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision.