| Revision as of 01:52, 2 March 2010 editRHB100 (talk | contribs)Extended confirmed users2,197 edits →Spherical symmetry: Removed repeated section.← Previous edit | Revision as of 04:43, 2 March 2010 edit undoOzob (talk | contribs)Extended confirmed users, Pending changes reviewers5,321 edits →Mathematical form: Corrections and copyedits. What does everyone think of this version?Next edit → | ||
| Line 6: | Line 6: | ||
| ==Mathematical form== | ==Mathematical form== | ||
| ⚫ | The ] ''V'' at a distance ''r'' from a ] of mass ''M'' is | ||
| ⚫ | :<math>V = -\frac{GM}{r},</math> | ||
| where ''G'' is the ]. ''V'' has units of energy per unit mass. ''V'' is always negative where it is defined, and as ''r'' tends to infinity, it approaches zero. | |||
| ⚫ | The ], and thus the acceleration of a small body in the space around the massive object, is the negative ] of the gravitational potential. Because the potential has no angular components, its gradient is: | ||
| ⚫ | :<math>\mathbf{a} = -\frac{GM}{r^3} \mathbf{r} = -\frac{GM}{r^2} \hat{\mathbf{r}},</math> | ||
| where '''r''' is a vector of length ''r'' pointing from the origin towards the small body and <math>\hat{\mathbf{r}}</math> is a unit vector pointing from the origin towards the small body. The magnitude of the acceleration therefore follows an ]: | |||
| ⚫ | :<math>|\mathbf{a}| = \frac{GM}{r^2}.</math> | ||
| The potential associated with a ] is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points '''x'''<sub>1</sub>, ..., '''x'''<sub>''n''</sub> and have masses ''m''<sub>1</sub>, ..., ''m''<sub>''n''</sub>, then the potential of the distribution at the point '''x''' is: | |||
| ⚫ | The ] V at |
||
| ⚫ | :<math>V(\mathbf{x}) = \sum_{i=1}^n -\frac{GM}{|\mathbf{x} - \mathbf{x_i}|}.</math> | ||
| If the mass distribution is given as a mass ] ''dm'' on three-dimensional ] '''R'''<sup>3</sup>, then the potential is the convolution of −G/|'''y'''| with ''dm''.<ref>{{harvnb|Vladimirov|1984|loc=§7.8}}</ref> In good cases this equals the integral | |||
| :<math>V(\mathbf{x}) = -\int_{\mathbf{R}^3} \frac{G}{|\mathbf{x} - \mathbf{y}|}\,dm(\mathbf{y}).</math> | |||
| If there is a continuous function ρ('''x''') representing the density of the distribution at '''x''', so that {{nowrap begin}}''dm'' = ρ('''x''')''d''<sup> 3</sup>''x''{{nowrap end}}, where ''d''<sup> 3</sup>''x'' is the Euclidean ], then the gravitational potential is | |||
| :<math>V(\mathbf{x}) = -\int_{\mathbf{R}^3} \frac{G}{|\mathbf{x}-\mathbf{y}|}\,\rho(\mathbf{y})\,d^3x.</math> | |||
| If ''V'' is a potential function coming from a continuous mass distribution ρ('''x'''), then ρ can be recovered using the ] Δ using the formula: | |||
| ⚫ | :<math>V = -\frac{GM}{r},</math> |
||
| :<math>\rho(\mathbf{x}) = \frac{1}{4\pi G}\Delta V(\mathbf{x}),</math> | |||
| This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure ''dm'' can be recovered in the same way if the Laplace operator is taken in the sense of ]s. Consequently the gravitational potential solves ]. | |||
| where ''M'' is the mass at point a and ''G'' is the ] (6.67428 × 10<sup>-11</sup> N (m/kg)<sup>2</sup>). | |||
| The potential, ''V'', has dimensions of energy per unit mass, and it approaches an upper limit of zero as r approaches infinity. | |||
| More generally, the potential associated with any ] is obtained by the superposition of potential associated with the individual masses. In the case of discrete point masses, this is the algebraic sum of the gravitational potentials. The potentialat point b is given by | |||
| :<math>V(\mathbf{r}) = -\sum_i \frac{GM_i}{|\mathbf{R}-\mathbf{r}_i|} \, \rm where \ \mathbf{r} = |\mathbf{R}-\mathbf{r}_i| \ </math> and where '''R''' is a vector from the center of mass to point b. | |||
| For the continuous case the potential, ''V'' at point b, is computed as an integral over the distributed mass, | |||
| :<math>V(\mathbf{r}) = - \int \frac{G}{|\mathbf{R}-\mathbf{x}|}\ dm </math> where dm equals density times differential volume and where '''x''' is a vector from the center of mass to the differential element of mass. | |||
| Expanding the denominator by taking the square root of the square, carrying out the dot product, and factoring R out of the denominator we get the more useful expression, | |||
| ⚫ | :<math>V(\mathbf{ |
||
| - \frac{1}{R}\int G \, / \, \sqrt{1 -2 cos( \beta ) \frac{x}{R} + \left( \frac{x}{R} \right)^2}\,dm.</math> | |||
| ⚫ | The ], and thus the acceleration of a |
||
| ⚫ | :<math> |
||
| The direction of the acceleration is towards the point mass. Thus the acceleration vector is | |||
| ⚫ | :<math>\mathbf{a} = -\frac{GM}{r^3} \mathbf{r} = -\frac{GM}{r^2} \hat{\mathbf{r}} |
||
| ==Spherical symmetry== | ==Spherical symmetry== | ||
Revision as of 04:43, 2 March 2010
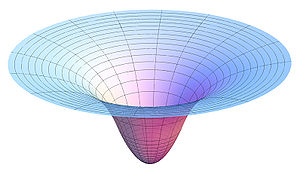
In celestial mechanics, the gravitational potential belonging to an individual massive object, such as the earth or the sun, is a scalar field generated by that object, see also gravitational well. It is in every way analogous to the electric potential with mass playing the role of charge; the gravitational field is analogous to the electric field, and so are their mathematics and properties.
In mathematics the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory.
Mathematical form
The potential V at a distance r from a point mass of mass M is
where G is the gravitational constant. V has units of energy per unit mass. V is always negative where it is defined, and as r tends to infinity, it approaches zero.
The gravitational field, and thus the acceleration of a small body in the space around the massive object, is the negative gradient of the gravitational potential. Because the potential has no angular components, its gradient is:
where r is a vector of length r pointing from the origin towards the small body and is a unit vector pointing from the origin towards the small body. The magnitude of the acceleration therefore follows an inverse square law:
The potential associated with a mass distribution is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points x1, ..., xn and have masses m1, ..., mn, then the potential of the distribution at the point x is:
If the mass distribution is given as a mass measure dm on three-dimensional Euclidean space R, then the potential is the convolution of −G/|y| with dm. In good cases this equals the integral
If there is a continuous function ρ(x) representing the density of the distribution at x, so that dm = ρ(x)dx, where dx is the Euclidean volume element, then the gravitational potential is
If V is a potential function coming from a continuous mass distribution ρ(x), then ρ can be recovered using the Laplace operator Δ using the formula:
This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of distributions. Consequently the gravitational potential solves Poisson's equation.
Spherical symmetry
A spherically symmetric mass distribution behaves to an observer completely outside the distribution as though all of the mass were concentrated at the center, and thus effectively as a point mass, by the shell theorem. On the surface of the Earth, the acceleration is given by so-called standard gravity g, approximately 9.8 m/s, although this value varies slightly with latitude and altitude: the magnitude of the acceleration is a little larger at the poles than at the equator because the Earth is an oblate spheroid.
Within a spherically symmetric mass distribution, it is possible to solve Poisson's equation in spherical coordinates. Within a uniform spherical body of radius R and density σ, the gravitational force g inside the sphere varies linearly with distance r from the center, giving the gravitational potential inside the sphere, which is
which smoothly connects to the potential function for the outside of the sphere (see the figure at the top).
Potential energy
The gravitational potential (V) is the potential energy (U) per unit mass:
where m is the mass of the object. The potential energy is the negative of the work done by the gravitational field moving the body to its given position in space from infinity. If the body has a mass of 1 unit, then the potential energy to be assigned to that body is equal to the gravitational potential. So the potential can be interpreted as the negative of the work done by the gravitational field moving a unit mass in from infinity.
In some situations the equations can be simplified by assuming a field which is nearly independent of position. For instance, in daily life, in the region close to the surface of the Earth, the gravitational acceleration can be considered constant. In that case the difference in potential energy from one height to another is to a good approximation linearly related to the difference in height:
General relativity
In general relativity, the gravitational potential is replaced by the metric tensor.
References
- Peter Dunsby (1996-06-15). "Mass in Newtonian theory". Tensors and Relativity: Chapter 5 Conceptual Basis of General Relativity. Department of Mathematics and Applied Mathematics University of Cape Town. Retrieved 2009-03-25.
- Lupei Zhu Associate Professor, Ph.D. (California Institute of Technology, 1998). "Gravity and Earth's Density Structure". EAS-437 Earth Dynamics. Saint Louis University (Department of Earth and Atmospheric Sciences). Retrieved 2009-03-25.
{{cite web}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - Charles D. Ghilani (2006-11-28). "The Gravity Field of the Earth". The Physics Fact Book. Penn State Surveying Engineering Program. Retrieved 2009-03-25.
- Rastall, Peter (1991). Postprincipia: Gravitation for Physicists and Astronomers. World Scientific. pp. 7ff. ISBN 9810207786.
- Vladimirov, V. S. (1971), Equations of mathematical physics, Translated from the Russian by Audrey Littlewood. Edited by Alan Jeffrey. Pure and Applied Mathematics, vol. 3, New York: Marcel Dekker Inc., MR0268497.
- Vladimirov 1984, §7.8 harvnb error: no target: CITEREFVladimirov1984 (help)


 is a unit vector pointing from the origin towards the small body. The magnitude of the acceleration therefore follows an
is a unit vector pointing from the origin towards the small body. The magnitude of the acceleration therefore follows an 






