| Revision as of 19:05, 5 February 2014 editStigmatella aurantiaca (talk | contribs)Extended confirmed users8,849 edits Reverted to revision 575257575 by Rursus: Multiple issues. A consensus developed between Patrick0Moran, 129.217.159.124 and myself that it would be best to start over from the version of 07:41, 1 October 2013. Please see talk page. (TW)← Previous edit | Revision as of 19:28, 5 February 2014 edit undoDParlevliet (talk | contribs)Extended confirmed users533 edits Undid revision 594085303 by Stigmatella aurantiaca (talk) Deletion of edits which are not argumented to be wrong is not allowed by Wiki rules.Next edit → | ||
| Line 1: | Line 1: | ||
| {{Quantum mechanics|cTopic=Experiments}} | {{Quantum mechanics|cTopic=Experiments}} | ||
| A '''delayed choice quantum eraser''' is a quantum eraser equipment in which the information is erased after detection. A quantum eraser is based on a two-path experiment (like ] or ]) in which the wave of (mostly) a photon is split in two waves, which follow different paths. If both waves combine again at a detector, it will measure an interference pattern. Quantum mechanics states that if it is known which path the photon particle followed, the interference disappears. A Quantum eraser first adds the which-path information, showed the disappearing of the interference, and then erases this information, causing the interference to appear again. In a Delayed choice quantum eraser the which-path information is erased after detection of the photon. This experiment was first proposed by ] and Drühl and performed by Kim e.a.<ref>name="Scully">{{cite journal | author = M.O. Scully and K. Drühl| journal = ] | volume = 25 | year = 1982 | pages = 2208}}</ref> | |||
| A '''delayed choice quantum eraser''', first performed by Yoon-Ho Kim, R. Yu, S.P. Kulik, Y.H. Shih and ],<ref name="DCQE">{{cite journal | author = Kim, Yoon-Ho | coauthors = R. Yu, S.P. Kulik, Y.H. Shih and Marlan Scully | title = A Delayed Choice Quantum Eraser | journal = ] | volume = 84 | year = 2000 | pages = 1–5 | doi = 10.1103/PhysRevLett.84.1| arxiv=quant-ph/9903047 | bibcode=2000PhRvL..84....1K}}</ref> and reported in early 1999, is an elaboration on a ] involving the concepts considered in ]. It was designed to investigate peculiar consequences of the well-known ] in quantum mechanics, as well as the consequences of ]. | |||
| .<ref name="DCQE">{{cite journal | author = Kim, Yoon-Ho | coauthors = R. Yu, S.P. Kulik, Y.H. Shih and Marlan Scully | title = A Delayed Choice Quantum Eraser | journal = ] | volume = 84 | year = 2000 | pages = 1–5 | doi = 10.1103/PhysRevLett.84.1| arxiv=quant-ph/9903047 | bibcode=2000PhRvL..84....1K}}</ref> The experiment was designed to investigate peculiar consequences of the double slit experiment in quantum mechanics, as well as the consequences of ]. | |||
| == |
==Experiments== | ||
| In the basic ], a very narrow beam of ] from a source that is far enough away to have almost perfectly parallel wave fronts<!-- too large infix subclause! -->, is directed perpendicularly towards a wall pierced by two parallel slit apertures. The widths of the slits and their separation are approximately the same size as the wavelength of the incident light. | |||
| ===Polarizers at the slits=== | |||
| If a detection screen (anything from a sheet of white paper to a digital camera) is put on the other side of the double slit wall, a pattern of light and dark fringes will be observed, a pattern that is called '''interference pattern'''. | |||
| A Quantum eraser which often used in education is based on placing two orthogonal polarizers at the slits of a Double slit experiment, causing the interference to disappear. Then after the slits a polarizer is placed at 45º, which erases the polarised information of the waves, showing the interference again. This experiment is described in ]. With classical waves the result can also be explained. | |||
| Early in the history of this experiment, scientists discovered that, by decreasing the brightness of the light source sufficiently, individual particles of light that form the interference pattern are detectable. They next tried to discover by which slit a given unit of light (]) had traveled. | |||
| ===Interferometer with 50% mirror=== | |||
| Unexpectedly, the results discovered were that if anything is done to permit determination of which path the photon takes, the interference pattern disappears: there is '''no''' interference pattern. Each photon simply hits the detector by going through one of the two slits. Each slit yields a simple single pile of hits; there is no interference pattern. | |||
| It is counterintuitive that a different outcome results based on whether or not the photon is constrained to follow one or another path well '''after''' it goes through the slit but before it hits the detector. | |||
| Two inconsistent accounts of the nature of light have long contended. The discovery of light's interfering with itself seemed to prove that light could not be a particle. It seemed that it had to be a wave to explain the interference seen in the double-slit experiment (first devised by ] in his classic ] of the eighteenth century). | |||
| In the early twentieth century, experiments with the ] (the phenomenon that makes the light meters in cameras possible) gave equally strong evidence to support the idea that light is a particle phenomenon. Nothing is observable regarding it between the time a photon is emitted (which experimenters can at least locate in time by determining the time at which energy was supplied to the electron emitter) and the time it appears as the delivery of energy to some detector screen (such as a ] or the emulsion of a film camera). | |||
| Nevertheless experimenters have tried to gain indirect information about which path a photon "really" takes when passing through the double-slit apparatus. | |||
| In the process they learned that constraining the path taken by one of a pair of ] photons inevitably controls the path taken by the partner photon. Further, if the partner photon is sent through a double-slit device and thus interferes with itself, then very surprisingly the first photon will also behave in a way consistent with its having interfered with itself, even though there is no double-slit device in its way. | |||
| In a ], one arranges to detect which one of the slits the photon passes through, but also to construct the experiment in such a way that this information can be "erased" after the fact. | |||
| In practice, this "erasure" of path information frequently means removing the constraints that kept photons following two different paths separated from each other. | |||
| In one experiment, rather than splitting one photon or its probability wave between two slits, the photon is subjected to a ]. If one thinks in terms of a stream of photons being randomly directed by such a beam splitter to go down two paths that are kept from interaction, it is clear that no photon can then interfere with any other or with itself. | |||
| {{clear}} | |||
| ] | ] | ||
| This Quantum eraser is the ], where a light beam (yellow) is split by a 50% mirror in two beams (red and blue). Both beams are reflected by a mirror and cross each other. Finally each beam ends in a separate detector.<ref>{{cite journal |last1=Jacques |first1=Vincent |last2=Wu |first2=E |last3=Grosshans|first3=Frédéric|last4=Treussart|first4=François|last5=Grangier|first5=Philippe|last6=Aspect|first6=Alain|last7=Rochl|first7=Jean-François|year=2007 |title=Experimental Realization of Wheeler's Delayed-Choice Gedanken Experiment |journal=Science |publisher= |pmid=17303748|volume=315 |issue=5814 |pages=pp. 966–968 |url=http://www.sciencemag.org/cgi/content/full/315/5814/966 |doi=10.1126/science.1136303 |arxiv = quant-ph/0610241 |bibcode = 2007Sci...315..966J }}</ref> | |||
| If the rate of photon production is reduced so that only one photon is entering the apparatus at any one time, however, it becomes impossible to understand the photon as only moving through one path because when their outputs are redirected so that they coincide on a common detector then interference phenomena appear. | |||
| In the |
In the top diagram only red or blue photons are detected, so no interference is measured. In the bottom diagram with a second beam splitter both outgoing beams has both red and blue photons, without possibility to distinguish, now showing interference in both detectors. The description is also valid for single photons. | ||
| In the classical wave description the wave of the photon is split in two by the 50% mirror. In the upper diagram each detector sees only one wave, so there is no interference with the other wave. In the lower diagram both waves are mixed, so each detector sees both waves, which interfere. The wave determines the possibility of absorption. | |||
| In the top diagram, one can see that the trajectories of photons are clearly known — in the sense that if a photon emerges at the top of the apparatus it appears that it had to have come by the path that leads to that point (blue line) and if it emerges at the side of the apparatus it appears that it had to have come by way of the other path (red line). | |||
| The phase difference is introduced along the two paths because of the different effects of passing through a glass plate, being reflected off its first surface, or passing through the back surface of a semi-silvered beam splitter and being reflected by the back (inner side) of the reflective surface. | |||
| Next, as shown in the bottom diagram, a second beam splitter is introduced at the top right. It can direct either beam towards either path; thus note that whatever emerges from each exit port may have come by way of either path. | |||
| It is in this sense that the path information has been "erased". | |||
| Note that total phase differences are introduced along the two paths because of the different effects of passing through a glass plate, being reflected off its first surface, or passing through the back surface of a semi-silvered beam splitter and being reflected by the back (inner side) of the reflective surface. | |||
| The result is that waves pass out of both the top upwards exit, and also the top-right exit. Specifically, waves passing out the top exit interfere destructively, whereas waves passing out the upper right side exit interfere constructively. | The result is that waves pass out of both the top upwards exit, and also the top-right exit. Specifically, waves passing out the top exit interfere destructively, whereas waves passing out the upper right side exit interfere constructively. | ||
| {{clear}} | |||
| ===With entangled photons and particle-path detectors (Kim e.a.)=== | |||
| A more detailed explanation of the phase changes involved here can be found in the ] article. Also, the experiment depicted above is reported in full in a reference.<ref>{{cite journal |last1=Jacques |first1=Vincent |last2=Wu |first2=E |last3=Grosshans|first3=Frédéric|last4=Treussart|first4=François|last5=Grangier|first5=Philippe|last6=Aspect|first6=Alain|last7=Rochl|first7=Jean-François|year=2007 |title=Experimental Realization of Wheeler's Delayed-Choice Gedanken Experiment |journal=Science |publisher= |pmid=17303748|volume=315 |issue=5814 |pages=pp. 966–968 |url=http://www.sciencemag.org/cgi/content/full/315/5814/966 |doi=10.1126/science.1136303 |arxiv = quant-ph/0610241 |bibcode = 2007Sci...315..966J }}</ref> | |||
| If the second beam splitter in the lower diagram could be inserted or removed one might assert that a photon must have traveled by way of one path or the other if a photon were detected at the end of one path or the other. The appearance would be that the photon "chose" one path or the other at the only (bottom left) beam splitter, and therefore could only arrive at the respective path end. | |||
| The subjective assurance that the photon followed a single path is brought into question, however, if (after the photon has presumably "decided" which path to take) a second beam splitter then makes it impossible to say by which path the photon has traveled. | |||
| What once appeared to be a "black and white" issue now appears to be a "gray" issue. It is the mixture of two originally separated paths that constitutes what is colloquially referred to as "erasure." It is actually more like "a return to indeterminability." | |||
| ==The experiment== | |||
| {{clear}} | {{clear}} | ||
| ] | ] | ||
| An experimental setup is as follows.<ref name="DCQE" /> A high intensity laser radiates a double slit (vertical black line in the upper left hand corner of the diagram). After the slits a ] crystal (BBO) causes ] (SPDC), which generates now and then two identical ] photons with 1/2 the frequency of the laser photons, in the "red" or "blue" area of the BBO. These photons are caused to diverge and follow two paths by a ]. | |||
| One of the photons, the "signal" photon, goes upwards, through a lens, to the target detector D<sub>0</sub>. | |||
| The photon goes through one (or both) of the two slits, whose paths are shown as red or light blue lines, indicating which slit the photon came through (red indicates slit A, light blue indicates slit B). | |||
| The other photon, the "idler" photon, goes downwards and is deflected by a prism that sends it along divergent paths, depending on whether it came from the "red" or "blue" BBO area. | |||
| So far, the experiment is like a conventional two-slit experiment. However, after the slits a ] crystal (labeled as BBO) causes ] (SPDC), converting the photon (from either slit) into two identical ] photons with 1/2 the frequency of the original photon. These photons are caused to diverge and follow two paths by the ]. | |||
| Beyond each path a 50% mirror acts as a ] (green blocks), resulting in a 50% chance to pass through and a 50% chance reflecting to detectors D<sub>3</sub> or D<sub>4</sub>. The photons which pass through are reflected by 100% mirrors (gray-green blocks) to the detectors D<sub>1</sub> or D<sub>2</sub>. Where both beams cross a third 50% mirror is placed, which reflect 50% of each beam to the other detector. | |||
| One of these photons, referred to as the "signal" photon (look at the red and light-blue lines going ''upwards'' from the Glan-Thompson prism), continues to the target detector called D<sub>0</sub>. The positions where these "signal" photons detected by D<sub>0</sub> occur can later be examined to discover if collectively those positions form an interference pattern. | |||
| Because of this arrangement: | |||
| The other entangled photon, referred to as the "idler" photon (look at the red and light-blue lines going ''downwards'' from the Glan-Thompson prism), is deflected by a prism that sends it along divergent paths depending on whether it came from slit A or slit B. | |||
| * If the photon is recorded at detector D<sub>3</sub>, it can only be a "blue" photon. | |||
| Somewhat beyond the path split ]s (green blocks) are encountered that each have a 50% chance of allowing the idler to pass through and a 50% chance of causing it to be reflected. The gray-green blocks in the diagram are mirrors. | |||
| * If the photon is recorded at detector D<sub>4</sub>, it can only be a "red" photon. | |||
| If the photon is recorded at detector D<sub>1</sub> or D<sub>2</sub>, it has a 50% chance to be a "blue" photon and 50% chance to be a "red" one. So when detected by D<sub>1</sub> or D<sub>2</sub>, one cannot know through which slit the photon has traveled. It is said that the red/blue information has been "erased". | |||
| Because of the way the beam splitters are arranged the idler can be detected by detectors labeled D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub> and D<sub>4</sub>. Note that: | |||
| '''''Observed results''''' | |||
| If it is recorded at detector D<sub>3</sub>, then it can only have come from slit B. | |||
| A ] selects from the target detector D<sub>0</sub> only the events which coincide with the other detectors. This includes a delay of 8 ] to compensate for the 2.5 meter longer path to the other detectors. | |||
| If it is recorded at detector D<sub>4</sub> it can only have come from slit A. | |||
| * When events were counted which coincided with D<sub>3</sub> or D<sub>4</sub>, there was no interference. | |||
| * When events were counted which coincided with D<sub>1</sub> or D<sub>2</sub>, there was an interference pattern. | |||
| This is in agreement with the statement in Quantum mechanics that when the path is known, the interference pattern disappears. But most remarkable is that the photons in D<sub>0</sub> seem to know that they will not form an interference pattern 8 ns ''before'' the path information is detected by D<sub>3</sub> or D<sub>4</sub>. This seems to suggest that the probability of photon detection depends on a future event. | |||
| Thus, which detector receives the idler photon either gives information as to whether the signal photon with which it is entangled went through slit A or B ("which-path information"), or implies that such information is not available (from this source). Insofar as which-path information was potentially available from the idler photon earlier, it is said that the information has been "erased". | |||
| With classical wave physics the absence of interference with D3/D4 can be explained, because when an photon is emitted in the red area of the BBO, there will be no wave in the blue area (and vice versa), so no two waves to interfere. However the appearance of the interference with D1/D2 cannot be explained classical. | |||
| By using a ] the experimenters were able to isolate the entangled signal from the overwhelming photo-noise of the laboratory, recording only events where both signal and idler photons were detected. | |||
| When the experimenters ''looked only at'' the signal photons whose entangled idlers were detected at D<sub>1</sub> or D<sub>2</sub>, they found an interference pattern. | |||
| However, when they looked at the signal photons whose entangled idlers were detected at D<sub>3</sub> or similarly at D<sub>4</sub>, ''they found no interference''. | |||
| This result is similar to that of the double-slit experiment since interference is observed when it is not known which slit the photon went through, while no interference is observed when the path is known. | |||
| However, what makes this experiment possibly astonishing is that, unlike in the classic double-slit experiment, the choice of whether to preserve or erase the which-path information of the idler need not be made until ''after'' the position of the signal photon has already been measured by D<sub>0</sub>. | |||
| There is never any which-path information determined directly for the photons that are detected at D<sub>0</sub>, yet detection of which-path information by D<sub>3</sub> or D<sub>4</sub> means that no interference pattern is observed in the corresponding subset of signal photons at D<sub>0</sub>. | |||
| The results from Kim, et al.<ref name="DCQE" /> have shown that whether the idler photon is detected at a detector that preserves its which-path information (D<sub>3</sub> or D<sub>4</sub>) or a detector that erases its which-path information (D<sub>1</sub> or D<sub>2</sub>) determines whether interference is seen at D<sub>0</sub>, even though the idler photon ''is not observed until after'' the signal photon arrives at D<sub>0</sub> due to the shorter optical path for the latter. | |||
| Some have interpreted this result to mean that the delayed choice to observe or not observe the path of the idler photon will change the outcome of an event in the past. However, an interference pattern may only be observed ''after'' the idlers have been detected (i.e., at D<sub>1</sub> or D<sub>2</sub>). | Some have interpreted this result to mean that the delayed choice to observe or not observe the path of the idler photon will change the outcome of an event in the past. However, an interference pattern may only be observed ''after'' the idlers have been detected (i.e., at D<sub>1</sub> or D<sub>2</sub>). | ||
| Line 94: | Line 57: | ||
| Note that the total pattern of all signal photons at D<sub>0</sub>, whose entangled idlers went to multiple different detectors, will never show interference regardless of what happens to the idler photons.<ref name="Greene">{{cite book | last = Greene | first = Brian | authorlink = Brian Greene | title = The Fabric of the Cosmos | publisher = Alfred A. Knopf | year = 2004 | isbn = 0-375-41288-3 | page = 198}}</ref> One can get an idea of how this works by looking carefully at both the graph of the subset of signal photons whose idlers went to detector D<sub>1</sub> (fig. 3 in the paper<ref name="DCQE" />), and the graph of the subset of signal photons whose idlers went to detector D<sub>2</sub> (fig. 4), and observing that the peaks of the first interference pattern line up with the troughs of the second and vice versa (noted in the paper as "a π phase shift between the two interference fringes"), so that the sum of the two will not show interference. | Note that the total pattern of all signal photons at D<sub>0</sub>, whose entangled idlers went to multiple different detectors, will never show interference regardless of what happens to the idler photons.<ref name="Greene">{{cite book | last = Greene | first = Brian | authorlink = Brian Greene | title = The Fabric of the Cosmos | publisher = Alfred A. Knopf | year = 2004 | isbn = 0-375-41288-3 | page = 198}}</ref> One can get an idea of how this works by looking carefully at both the graph of the subset of signal photons whose idlers went to detector D<sub>1</sub> (fig. 3 in the paper<ref name="DCQE" />), and the graph of the subset of signal photons whose idlers went to detector D<sub>2</sub> (fig. 4), and observing that the peaks of the first interference pattern line up with the troughs of the second and vice versa (noted in the paper as "a π phase shift between the two interference fringes"), so that the sum of the two will not show interference. | ||
| {{clear}} | |||
| === Explanation by physical optics === | |||
| {{clear}} | |||
| By examining the positions of signal photons at detector D<sub>0</sub>, which correspond to idler photons at D<sub>1</sub> or D<sub>2</sub>, an interference pattern is found in the recorded data. There seems to be a misconception, where this pattern originates from. One might think, the signal photons shape the pattern on the way to detector D<sub>0</sub> by interfering with each other. But at detector D<sub>0</sub> only a blurred image of the double slit is projected by the converging lens, effectively smearing any direct interference patterns from the slits. | |||
| ===With entangled photons and circular polarizers (Walborn e.a.)=== | |||
| To understand the source of the derived interference pattern, one has to focus on the third beam splitter BS<sub>C</sub>, where the photon paths from both slits merge. At this point a phase difference exists between the merging paths, which is dependent on the different path lengths from slit A or B respectively to the splitter. Furthermore path length and phase difference depend in part on the deviation angle of the idler photon leaving the Glan-Thompson prism. While a fixed position on detector D<sub>0</sub> is correlated to events at detector D<sub>1</sub> or D<sub>2</sub>, only events at D<sub>1</sub> or D<sub>2</sub> are inspected, which share the same phase differences. After leaving the beam splitter BS<sub>C</sub>, each phase difference may lead to constructive or destructive interference on the paths from the splitter to the detectors D<sub>1</sub> and D<sub>2</sub>, while also allowing any arbitrary intermediate values. But one has to note, that the combined probabilities for both paths behind BS<sub>C</sub> always add up to 1, as the difference of the phase shifts between that paths amounts to π or 180°. | |||
| ] | |||
| By changing the detector D<sub>0</sub> position, different phase shifts at detector D<sub>1</sub> and D<sub>2</sub> lead to a different statistic in observed correlated events: A derived interference pattern builds up in the data. Consequently the derived patterns from detectors D<sub>1</sub> and D<sub>2</sub> add up to the Gaussian distribution, which is observed with the detectors D<sub>3</sub> and D<sub>4</sub>. | |||
| In this Delayed quantum eraser a ] (BBO) crystal, radiated by a strong laser, will generate now and then two entangled photons.<ref name=Walborn>{{cite journal | last =Walborn | first =S. P. | coauthors =M.O. Terra Cunha and C.H. Monken. | title =Double-Slit Quantum Eraser | journal =Phys. Rev. A | volume =65 | issue =3 | pages =033818 | year =2002 | url =http://arxiv-web3.library.cornell.edu/abs/quant-ph/0106078 | doi =10.1103/PhysRevA.65.033818 | url=http://www.arxiv.org/pdf/quant-ph/0106078%E2%80%8E}}</ref> One photon (yellow path) goes through a double slit to signal detector Ds, with ] Q1 or Q2 in each path. They are rotated 90° to each other, producing a ] in opposite directions. The other photon (green path) goes to detector Dp, with a ] cube POL in the path. Only photons in Ds are registered which ] with photons in Dp. Dp is situated closer to the BBO then Ds, so photons are first detected by Dp. The results were: | |||
| # Without Q1/Q2 and POL there was an interference pattern in Ds | |||
| Data from events correlated with photons at detectors D<sub>3</sub> and D<sub>4</sub> show no derived interference patterns, because there is no interference of different photon paths from both slits in the first place. | |||
| # With Q1/Q2 there was no interference. | |||
| # With Q1/Q2 and POL, adjusted on the Q1 fast axis, there was interference. | |||
| # With Q1/Q2 and POL, adjusted on the Q2 fast axis, there was interference, but 180º shifted with 3. | |||
| # 1-4 with Dp on a larger distance then Ds gives the same result. This is a delayed eraser, because the photon in Dp is detected later then in Ds | |||
| The explanation with quantum mechanics is that Q1/Q2 marks the red path and the blue path beams. So one could detect which path the photon went, also when this measurement is not actually done (as in 2). This removes the interference pattern. When placing POL at a suitable angle, the polarization information is erased, so it is no longer possible to know by which path the photon travelled. Therefore the interference pattern is restored. | |||
| === Time relations among data === | |||
| ] | |||
| ] By noting which photons reaching Detector 0 correspond with photons reaching Detectors 1, 2, 3, and 4, it is possible to sort photon records collected by Detector 0 into four groups. Only then will it become possible to see interference patterns in two groups and only diffraction patterns in the other two groups. If there were no coincidence counter, then there would be no way to distinguish any photon that arrives at Detector 0 from any other photon that reaches it. | |||
| ] | |||
| Photons will not reach detectors one through four in regular rotation, so the only way to sort out the photons that are entangled twins with the ones that reached each of those detectors is to group them according to which of those four detectors was activated when a photon reached Detector 0. Note that in the schematic diagrams the fringes or interference patterns imaged by Detector 1 and Detector 2 will add together to form a solid band. The addition of the diffraction patterns paired with the diffraction patterns seen by Detector 3 and Detector 4 will make the center area somewhat brighter than it would otherwise be, but would have no other influence on the confused picture produced by the raw data gathered at Detector 0. | |||
| In the classical wave description Q1 and Q2 are ] which have ] a "fast" and "slow" axis. The slow axis has 90° phase delay to the fast axis. The axis of Q1 and Q2 are orthogonal (see figure). In 3 and 4 the POL forces the idler wave in a certain direction. Because of entanglement the signal wave will be forced at 90° of the idler wave.<ref name=Walborn></ref> In 3 the POL forces the signal wave polarization to be parallel to the fast axis of Q2. Then the output polarisation does not rotate, but is linear, with Q1 having -90° phase shift (slow axis) with Q2.<ref>see ]</ref> In 4 Q1 is +90° phase shift with Q2. Therefore 3 and 4 gives interference patterns which are 180° shifted, as has been measured. In 2 the incoming polarization can be resolve in two polarizations on the F and S axis, which each give the same result as 3 en 4. So 2 is not an absence of interference, but the sum of two interference patterns which are shifted 180°. With waves the crucial moments are not the detection, but the polarisers. In there is no delayed choice, but the property of entangled photons that if POL changes the polarization of the idler photon. The signal photon will follow ''directly'', also in front of Q1/Q2, although these are situated closer to the BBO then POL. | |||
| It is impossible to know which group a photon appearing at Detector 0 at time T<sub>1</sub> may belong to until '''after''' its entangled partner is found at one of the other detectors and their coincidence is measured at some slightly later time T<sub>2</sub>. | |||
| ==Discussion== | ==Discussion== | ||
| === Problems with using retrocausality === | |||
| {{Unreferenced section|date=August 2012|reason=This section is a nice and clear description of the problem with retrocausality, however, without any reference to the source there is no way of getting a deeper background on the explanation}} | |||
| This delayed choice quantum eraser experiment raises questions about time, time sequences, and thereby brings our usual ideas of time and causal sequence into question. If a determining factor in the complicated (lower) part of the apparatus determines an outcome in the simple part of the apparatus that consists of only a lens and a detection screen, then effect seems to precede cause. So if the light paths involved in the complicated part of the apparatus were greatly extended in order that, e.g., a year might go by before a photon showed up at D<sub>1</sub>, D<sub>2</sub>, D<sub>3</sub>, or D<sub>4</sub>, then when a photon showed up in one of these detectors it would cause the photon in the upper, simple part of the apparatus to have shown up in a certain mode a year earlier. Perhaps by re-routing light paths to the four detectors during that one year so that the number of possible outcomes is reduced to two or even perhaps to one, then the experimenter could send a signal back through time. Changing between the first possible arrangement and second possible arrangement of parts in the complicated part of the experiment would then function like the opening and closing of a telegraph key. | |||
| === Details pertaining to retrocausality in the Kim experiment === | === Details pertaining to retrocausality in the Kim experiment === | ||
Revision as of 19:28, 5 February 2014
| Part of a series of articles about |
| Quantum mechanics |
|---|
| Schrödinger equation |
| Background |
| Fundamentals |
| Experiments |
| Formulations |
| Equations |
| Interpretations |
| Advanced topics |
Scientists
|
A delayed choice quantum eraser is a quantum eraser equipment in which the information is erased after detection. A quantum eraser is based on a two-path experiment (like double slit experiment or interferometer) in which the wave of (mostly) a photon is split in two waves, which follow different paths. If both waves combine again at a detector, it will measure an interference pattern. Quantum mechanics states that if it is known which path the photon particle followed, the interference disappears. A Quantum eraser first adds the which-path information, showed the disappearing of the interference, and then erases this information, causing the interference to appear again. In a Delayed choice quantum eraser the which-path information is erased after detection of the photon. This experiment was first proposed by Scully and Drühl and performed by Kim e.a. . The experiment was designed to investigate peculiar consequences of the double slit experiment in quantum mechanics, as well as the consequences of quantum entanglement.
Experiments
Polarizers at the slits
A Quantum eraser which often used in education is based on placing two orthogonal polarizers at the slits of a Double slit experiment, causing the interference to disappear. Then after the slits a polarizer is placed at 45º, which erases the polarised information of the waves, showing the interference again. This experiment is described in double slit experiment. With classical waves the result can also be explained.
Interferometer with 50% mirror

This Quantum eraser is the Mach-Zehnder interferometer, where a light beam (yellow) is split by a 50% mirror in two beams (red and blue). Both beams are reflected by a mirror and cross each other. Finally each beam ends in a separate detector.
In the top diagram only red or blue photons are detected, so no interference is measured. In the bottom diagram with a second beam splitter both outgoing beams has both red and blue photons, without possibility to distinguish, now showing interference in both detectors. The description is also valid for single photons.
In the classical wave description the wave of the photon is split in two by the 50% mirror. In the upper diagram each detector sees only one wave, so there is no interference with the other wave. In the lower diagram both waves are mixed, so each detector sees both waves, which interfere. The wave determines the possibility of absorption.
The phase difference is introduced along the two paths because of the different effects of passing through a glass plate, being reflected off its first surface, or passing through the back surface of a semi-silvered beam splitter and being reflected by the back (inner side) of the reflective surface.
The result is that waves pass out of both the top upwards exit, and also the top-right exit. Specifically, waves passing out the top exit interfere destructively, whereas waves passing out the upper right side exit interfere constructively.
With entangled photons and particle-path detectors (Kim e.a.)
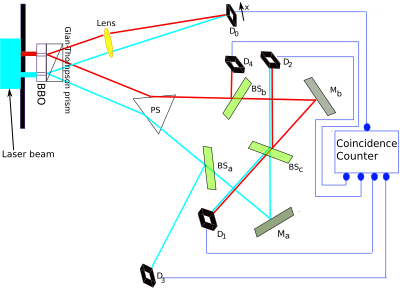
An experimental setup is as follows. A high intensity laser radiates a double slit (vertical black line in the upper left hand corner of the diagram). After the slits a beta barium borate crystal (BBO) causes spontaneous parametric down conversion (SPDC), which generates now and then two identical entangled photons with 1/2 the frequency of the laser photons, in the "red" or "blue" area of the BBO. These photons are caused to diverge and follow two paths by a Glan-Thompson Prism.
One of the photons, the "signal" photon, goes upwards, through a lens, to the target detector D0.
The other photon, the "idler" photon, goes downwards and is deflected by a prism that sends it along divergent paths, depending on whether it came from the "red" or "blue" BBO area.
Beyond each path a 50% mirror acts as a beam splitter (green blocks), resulting in a 50% chance to pass through and a 50% chance reflecting to detectors D3 or D4. The photons which pass through are reflected by 100% mirrors (gray-green blocks) to the detectors D1 or D2. Where both beams cross a third 50% mirror is placed, which reflect 50% of each beam to the other detector.
Because of this arrangement:
- If the photon is recorded at detector D3, it can only be a "blue" photon.
- If the photon is recorded at detector D4, it can only be a "red" photon.
If the photon is recorded at detector D1 or D2, it has a 50% chance to be a "blue" photon and 50% chance to be a "red" one. So when detected by D1 or D2, one cannot know through which slit the photon has traveled. It is said that the red/blue information has been "erased".
Observed results
A coincidence counter selects from the target detector D0 only the events which coincide with the other detectors. This includes a delay of 8 ns to compensate for the 2.5 meter longer path to the other detectors.
- When events were counted which coincided with D3 or D4, there was no interference.
- When events were counted which coincided with D1 or D2, there was an interference pattern.
This is in agreement with the statement in Quantum mechanics that when the path is known, the interference pattern disappears. But most remarkable is that the photons in D0 seem to know that they will not form an interference pattern 8 ns before the path information is detected by D3 or D4. This seems to suggest that the probability of photon detection depends on a future event.
With classical wave physics the absence of interference with D3/D4 can be explained, because when an photon is emitted in the red area of the BBO, there will be no wave in the blue area (and vice versa), so no two waves to interfere. However the appearance of the interference with D1/D2 cannot be explained classical.
Some have interpreted this result to mean that the delayed choice to observe or not observe the path of the idler photon will change the outcome of an event in the past. However, an interference pattern may only be observed after the idlers have been detected (i.e., at D1 or D2).
Note that the total pattern of all signal photons at D0, whose entangled idlers went to multiple different detectors, will never show interference regardless of what happens to the idler photons. One can get an idea of how this works by looking carefully at both the graph of the subset of signal photons whose idlers went to detector D1 (fig. 3 in the paper), and the graph of the subset of signal photons whose idlers went to detector D2 (fig. 4), and observing that the peaks of the first interference pattern line up with the troughs of the second and vice versa (noted in the paper as "a π phase shift between the two interference fringes"), so that the sum of the two will not show interference.
With entangled photons and circular polarizers (Walborn e.a.)

In this Delayed quantum eraser a beta barium borate (BBO) crystal, radiated by a strong laser, will generate now and then two entangled photons. One photon (yellow path) goes through a double slit to signal detector Ds, with circular polarizer Q1 or Q2 in each path. They are rotated 90° to each other, producing a circular polarization in opposite directions. The other photon (green path) goes to detector Dp, with a linear polarizer cube POL in the path. Only photons in Ds are registered which coincide with photons in Dp. Dp is situated closer to the BBO then Ds, so photons are first detected by Dp. The results were:
- Without Q1/Q2 and POL there was an interference pattern in Ds
- With Q1/Q2 there was no interference.
- With Q1/Q2 and POL, adjusted on the Q1 fast axis, there was interference.
- With Q1/Q2 and POL, adjusted on the Q2 fast axis, there was interference, but 180º shifted with 3.
- 1-4 with Dp on a larger distance then Ds gives the same result. This is a delayed eraser, because the photon in Dp is detected later then in Ds
The explanation with quantum mechanics is that Q1/Q2 marks the red path and the blue path beams. So one could detect which path the photon went, also when this measurement is not actually done (as in 2). This removes the interference pattern. When placing POL at a suitable angle, the polarization information is erased, so it is no longer possible to know by which path the photon travelled. Therefore the interference pattern is restored.
In the classical wave description Q1 and Q2 are quarter-wave plates which have orthogonal a "fast" and "slow" axis. The slow axis has 90° phase delay to the fast axis. The axis of Q1 and Q2 are orthogonal (see figure). In 3 and 4 the POL forces the idler wave in a certain direction. Because of entanglement the signal wave will be forced at 90° of the idler wave. In 3 the POL forces the signal wave polarization to be parallel to the fast axis of Q2. Then the output polarisation does not rotate, but is linear, with Q1 having -90° phase shift (slow axis) with Q2. In 4 Q1 is +90° phase shift with Q2. Therefore 3 and 4 gives interference patterns which are 180° shifted, as has been measured. In 2 the incoming polarization can be resolve in two polarizations on the F and S axis, which each give the same result as 3 en 4. So 2 is not an absence of interference, but the sum of two interference patterns which are shifted 180°. With waves the crucial moments are not the detection, but the polarisers. In there is no delayed choice, but the property of entangled photons that if POL changes the polarization of the idler photon. The signal photon will follow directly, also in front of Q1/Q2, although these are situated closer to the BBO then POL.
Discussion
Details pertaining to retrocausality in the Kim experiment
In their paper, Kim, et al. explain that the concept of complementarity is one of the most basic principles of quantum mechanics. According to the Heisenberg Uncertainty Principle, it is not possible to precisely measure both the position and the momentum of a quantum particle at the same time. In other words, position and momentum are complementary. In 1927, Niels Bohr maintained that quantum particles have both "wave-like" behavior and "particle-like" behavior, but can exhibit only one kind of behavior under conditions that prevent exhibiting the complementary characteristics. This complementarity has come to be known as the wave-particle duality of quantum mechanics. Richard Feynman believed that the presence of these two aspects under conditions that prevent their simultaneous manifestation is the basic mystery of quantum mechanics.
According to Kim, et al., "The actual mechanisms that enforce complementarity vary from one experimental situation to another." In the double-slit experiment, the common wisdom is that complementarity makes it seemingly impossible to determine which slit the photon passes through without at the same time disturbing it enough to destroy the interference pattern. A 1982 paper by Scully and Drühl circumvented the issue of disturbance due to direct measurement of the photon, according to Kim, et al. Scully and Drühl "found a way around the position-momentum uncertainty obstacle and proposed a quantum eraser to obtain which-path or particle-like information without introducing large uncontrolled phase factors to disturb the interference."
Scully and Drühl found that there is no interference pattern when which-path information is obtained, even if this information was obtained without directly observing the original photon, but that if you somehow "erase" the which-path information, an interference pattern is again observed.
In the delayed choice quantum eraser discussed here, the pattern exists even if the which-path information is erased shortly later in time than the signal photons hit the primary detector. However, the interference pattern can only be seen retroactively once the idler photons have already been detected and the experimenter has obtained information about them, with the interference pattern being seen when the experimenter looks at particular subsets of signal photons that were matched with idlers that went to particular detectors.
The main stumbling block for using retrocausality to communicate information
The total pattern of signal photons at the primary detector never shows interference, so it is not possible to deduce what will happen to the idler photons by observing the signal photons alone, which would open up the possibility of gaining information faster-than-light (since one might deduce this information before there had been time for a message moving at the speed of light to travel from the idler detector to the signal photon detector) or even gaining information about the future (since as noted above, the signal photons may be detected at an earlier time than the idlers), both of which would qualify as violations of causality in physics. The apparatus under discussion here could not communicate information in a retro-causal manner because it takes another signal, one which must arrive via a process that can go no faster than the speed of light, to sort the superimposed data in the signal photons into four streams that reflect the states of the idler photons at their four distinct detection screens.
In fact, a theorem proved by Phillippe Eberhard shows that if the accepted equations of relativistic quantum field theory are correct, it should never be possible to experimentally violate causality using quantum effects (see reference for a treatment emphasizing the role of conditional probabilities).
Yet there are those who persevere in attempting to communicate retroactively
Some physicists have speculated about the possibility that these experiments might be changed in a way that would be consistent with previous experiments, yet which could allow for experimental causality violations.
See also
- Afshar experiment
- Wheeler's delayed choice experiment
- The transactional interpretation of quantum mechanics
- Retrocausality
- Quantum radar
- Wheeler-Feynman absorber theory
References
- name="Scully">M.O. Scully and K. Drühl (1982). Physical Review A. 25: 2208.
{{cite journal}}: Missing or empty|title=(help) - ^ Kim, Yoon-Ho (2000). "A Delayed Choice Quantum Eraser". Physical Review Letters. 84: 1–5. arXiv:quant-ph/9903047. Bibcode:2000PhRvL..84....1K. doi:10.1103/PhysRevLett.84.1.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Jacques, Vincent; Wu, E; Grosshans, Frédéric; Treussart, François; Grangier, Philippe; Aspect, Alain; Rochl, Jean-François (2007). "Experimental Realization of Wheeler's Delayed-Choice Gedanken Experiment". Science. 315 (5814): pp. 966–968. arXiv:quant-ph/0610241. Bibcode:2007Sci...315..966J. doi:10.1126/science.1136303. PMID 17303748.
{{cite journal}}:|pages=has extra text (help) - Greene, Brian (2004). The Fabric of the Cosmos. Alfred A. Knopf. p. 198. ISBN 0-375-41288-3.
- ^ Walborn, S. P. (2002). "Double-Slit Quantum Eraser". Phys. Rev. A. 65 (3): 033818. doi:10.1103/PhysRevA.65.033818.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - see Waveplate#Quarter-wave plate
- Scully, Marlan O. (1982). "Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics". Physical Review A. 25 (4): 2208–2213. Bibcode:1982PhRvA..25.2208S. doi:10.1103/PhysRevA.25.2208.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Eberhard, Phillippe H. (1989). "Quantum field theory cannot provide faster-than-light communication". Foundations of Physics Letters. 2 (2): p. 127–149. Bibcode:1989FoPhL...2..127E. doi:10.1007/BF00696109.
{{cite journal}}:|pages=has extra text (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Bram Gaasbeek. Demystifying the Delayed Choice Experiments. arXiv preprint, 22 July 2010.
- John G. Cramer. NASA Goes FTL - Part 2: Cracks in Nature's FTL Armor. "Alternate View" column, Analog Science Fiction and Fact, February 1995.
- Paul J. Werbos, Ludmila Dolmatova. The Backwards-Time Interpretation of Quantum Mechanics - Revisited With Experiment. arXiv preprint, 7 August 2000.
External links
- presentation of the experiment
- basic delayed choice experiment
- delayed choice quantum eraser
- the notebook of philosophy and physics
- Comprehensive experimental test of quantum erasure, Alexei Trifonov, Gunnar Bjork, Jonas Soderholm, and Tedros Tsegaye (doi:10.1140/epjd/e20020030)
- A non-local quantum eraser (June 2012; 12 authors, including Anton Zeilinger)
