Misplaced Pages

Revision as of 14:34, 14 August 2016

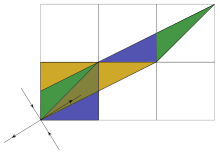
In mathematics, Arnold's cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effects in the 1960s using an image of a cat, hence the name.

Thinking of the torus ${\displaystyle \mathbb {T} ^{2}}$ as the quotient space ${\displaystyle \mathbb {R} ^{2}/\mathbb {Z} ^{2}}$, Arnold's cat map is the transformation ${\displaystyle \Gamma :\mathbb {T} ^{2}\to \mathbb {T} ^{2}}$ given by the formula

${\displaystyle \Gamma \,:\,(x,y)\to (2x+y,x+y){\bmod {1}}.}$

Equivalently, in matrix notation, this is

${\displaystyle \Gamma \left({\begin{bmatrix}x\\y\end{bmatrix}}\right)={\begin{bmatrix}2&1\\1&1\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}{\bmod {1}}={\begin{bmatrix}1&1\\0&1\end{bmatrix}}{\begin{bmatrix}1&0\\1&1\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}{\bmod {1}}.}$

That is, with a unit . equal to the width of the square image, the image is sheared one unit up, then one unit to the right, and all that lies outside that unit square is shifted back by the unit until it's within the square.

Properties

• Γ is invertible because the matrix has determinant 1 and therefore its inverse has integer entries,
• Γ is area preserving,
• Γ has a unique hyperbolic fixed point (the vertices of the square). The linear transformation which defines the map is hyperbolic: its eigenvalues are irrational numbers, one greater and the other smaller than 1 (in absolute value), so they are associated respectively to an expanding and a contracting eigenspace which are also the stable and unstable manifolds. The eigenspace are orthogonal because the matrix is symmetric. Since the eigenvectors have rationally independent components both the eigenspaces densely cover the torus. Arnold's cat map is a particularly well-known example of a hyperbolic toral automorphism, which is an automorphism of a torus given by a square unimodular matrix having no eigenvalues of absolute value 1.
• The set of the points with a periodic orbit is dense on the torus. Actually a point is preperiodic if and only if its coordinates are rational.
• Γ is topologically transitive (i.e. there is a point whose orbit is dense, this happens for example for any points on the expanding eigenspace)
• The number of points with period ${\displaystyle n}$ is exactly ${\displaystyle |\lambda _{1}^{n}+\lambda _{2}^{n}-2|}$ (where ${\displaystyle \lambda _{1}}$ and ${\displaystyle \lambda _{2}}$ are the eigenvalues of the matrix). For example, the first few terms of this series are 1, 5, 16, 45, 121, 320, 841, 2205 .... (The same equation holds for any unimodular hyperbolic toral automorphism if the eigenvalues are replaced.)
• Γ is ergodic and mixing,
• Γ is an Anosov diffeomorphism and in particular it is structurally stable.

The discrete cat map

It is possible to define a discrete analogue of the cat map. One of this map's features is that image being apparently randomized by the transformation but returning to its original state after a number of steps. As can be seen in the picture to the right, the original image of the cat is sheared and then wrapped around in the first iteration of the transformation. After some iterations, the resulting image appears rather random or disordered, yet after further iterations the image appears to have further order—ghost-like images of the cat, multiple smaller copies arranged in a repeating structure and even upside-down copies of the original image—and ultimately returns to the original image.

The discrete cat map describes the phase space flow corresponding to the discrete dynamics of a bead hopping from site q_t (0 ≤ q_t < N) to site q_t+1 on a circular ring with circumference N, according to the second order equation:

${\displaystyle q_{t+1}-3q_{t}+q_{t-1}=0\mod N}$

Defining the momentum variable p_t = q_t - q_t-1, the above second order dynamics can be re-written as a mapping of the square 0 ≤ q, p < N (the phase space of the discrete dynamical system) onto itself:

${\displaystyle q_{t+1}=2q_{t}+p_{t}\mod N}$

${\displaystyle p_{t+1}=q_{t}+p_{t}\mod N}$

This Arnold cat mapping shows mixing behavior typical for chaotic systems. However, since the transformation has a determinant equal to unity, it is area-preserving and therefore invertible the inverse transformation being:

${\displaystyle q_{t-1}=q_{t}-p_{t}\mod N}$

${\displaystyle p_{t-1}=-q_{t}+2p_{t}\mod N}$

For real variables q and p, it is common to set N = 1. In that case a mapping of the unit square with periodic boundary conditions onto itself results.

When N is set to an integer value, the position and momentum variables can be restricted to integers and the mapping becomes a mapping of a toroidial square grid of points onto itself. Such an integer cat map is commonly used to demonstrate mixing behavior with Poincaré recurrence utilising digital images. The number of iterations needed to restore the image can be shown never to exceed 3N.

For an image, the relationship between iterations could be expressed as follows:

${\displaystyle {\begin{array}{rrcl}n=0:\quad &T^{0}(x,y)&=&{\mbox{Input Image}}(x,y)\\n=1:\quad &T^{1}(x,y)&=&T^{0}\left({\bmod {(}}2x+y,N),{\bmod {(}}x+y,N)\right)\\&&\vdots \\n=k:\quad &T^{k}(x,y)&=&T^{k-1}\left({\bmod {(}}2x+y,N),{\bmod {(}}x+y,N)\right)\\&&\vdots \\n=m:\quad &{\mbox{Output Image}}(x,y)&=&T^{m}(x,y)\end{array}}}$

See also

• List of chaotic maps
• Recurrence plot

References

1. Vladimir I. Arnold; A. Avez (1967). Problèmes Ergodiques de la Mécanique Classique (in French). Paris: Gauthier-Villars.; English translation: V. I. Arnold; A. Avez (1968). Ergodic Problems in Classical Mechanics. New York: Benjamin.
2. Franks, John M (October 1977). "Invariant sets of hyperbolic toral automorphisms". American Journal of Mathematics. 99 (5). The Johns Hopkins University Press: 1089–1095. doi:10.2307/2374001. ISSN 0002-9327.
3. Sloane, N. J. A. (ed.). "Sequence A004146". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
4. Dyson, Freeman John; Falk, Harold (1992). "Period of a Discrete Cat Mapping". The American Mathematical Monthly. 99 (7). Mathematical Association of America: 603–614. doi:10.2307/2324989. ISSN 0002-9890. JSTOR 2324989.

External links

• Weisstein, Eric W. "Arnold's Cat Map". MathWorld.
• Effect of randomisation of initial conditions on recurrence time
• Arnold's Cat Map by Enrique Zeleny, The Wolfram Demonstrations Project.

v t e Chaos theory
Concepts	Core Attractor Bifurcation Fractal Limit set Lyapunov exponent Orbit Periodic point Phase space Anosov diffeomorphism Arnold tongue axiom A dynamical system Bifurcation diagram Box-counting dimension Correlation dimension Conservative system Ergodicity False nearest neighbors Hausdorff dimension Invariant measure Lyapunov stability Measure-preserving dynamical system Mixing Poincaré section Recurrence plot SRB measure Stable manifold Topological conjugacy Theorems Ergodic theorem Liouville's theorem Krylov–Bogolyubov theorem Poincaré–Bendixson theorem Poincaré recurrence theorem Stable manifold theorem Takens's theorem
Theoretical branches	Bifurcation theory Control of chaos Dynamical system Ergodic theory Quantum chaos Stability theory Synchronization of chaos
Chaotic maps (list)	Discrete Arnold's cat map Baker's map Complex quadratic map Coupled map lattice Duffing map Dyadic transformation Dynamical billiards outer Exponential map Gauss map Gingerbreadman map Hénon map Horseshoe map Ikeda map Interval exchange map Irrational rotation Kaplan–Yorke map Langton's ant Logistic map Standard map Tent map Tinkerbell map Zaslavskii map Continuous Double scroll attractor Duffing equation Lorenz system Lotka–Volterra equations Mackey–Glass equations Rabinovich–Fabrikant equations Rössler attractor Three-body problem Van der Pol oscillator
Physical systems	Chua's circuit Convection Double pendulum Elastic pendulum FPUT problem Hénon–Heiles system Kicked rotator Multiscroll attractor Population dynamics Swinging Atwood's machine Tilt-A-Whirl Weather
Chaos theorists	Michael Berry Rufus Bowen Mary Cartwright Chen Guanrong Leon O. Chua Mitchell Feigenbaum Peter Grassberger Celso Grebogi Martin Gutzwiller Brosl Hasslacher Michel Hénon Svetlana Jitomirskaya Bryna Kra Edward Norton Lorenz Aleksandr Lyapunov Benoît Mandelbrot Hee Oh Edward Ott Henri Poincaré Itamar Procaccia Mary Rees Otto Rössler David Ruelle Caroline Series Yakov Sinai Oleksandr Mykolayovych Sharkovsky Nina Snaith Floris Takens Audrey Terras Mary Tsingou Marcelo Viana Amie Wilkinson James A. Yorke Lai-Sang Young
Related articles	Butterfly effect Complexity Edge of chaos Predictability Santa Fe Institute

• Chaotic maps
• Exactly solvable models