| Revision as of 08:30, 12 August 2017 edit124.154.166.56 (talk)No edit summary← Previous edit | Revision as of 08:31, 12 August 2017 edit undo124.154.166.56 (talk) →Theory and originNext edit → | ||
| Line 10: | Line 10: | ||
| ==Theory and origin== | ==Theory and origin== | ||
| {{Quote box | |||
| |quote = One fact should be emphasized from the outset: while the various theoretical predictions about the superheavy nuclei differ as to the expected half-lives and regions of stability, all theoretical predictions are in agreement: superheavy nuclei can exist. Thus, the search for superheavy nuclei remains as a unique, rigorous test of the predictive power of modern theories of the structure of nuclei. | |||
| |source = — Seaborg and Loveland, 1987.<ref>{{Cite journal |last1=Seaborg |first1=G. T. |year=1987 |title=Superheavy elements |journal=] |volume=28 |issue= |pages=33–48 |bibcode=1987ConPh..28...33S |doi=10.1080/00107518708211038}}</ref> | |||
| |width = 220px | |||
| }} | |||
| The possibility of an "island of stability" was first proposed by ] in the late 1960s.<ref>{{cite web |title=The Island of Stability? |url=http://www.guerrillaexplorer.com/2011/11/island-of-stability.html |accessdate=2012-07-24}}</ref><!-- 1969? --> The hypothesis is based upon the ], which implies that the ] is built up in "shells" in a manner similar to the structure of the much larger electron shells in atoms. In both cases, shells are just groups of quantum ]s that are relatively close to each other. Energy levels from quantum states in two different shells will be separated by a relatively large energy gap, so when the number of ]s and ]s completely fills the ]s of a given shell in the nucleus, the ] per nucleon will reach a local maximum and thus that particular configuration will have a longer lifetime than nearby nuclides that do not possess filled shells.<ref>{{cite web |last=Nave |first=R. |date=|title=Shell Model of Nucleus |work=] |publisher=Department of Physics and Astronomy, ] |url=http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/shell.html |accessdate=22 January 2007 }}</ref> | The possibility of an "island of stability" was first proposed by ] in the late 1960s.<ref>{{cite web |title=The Island of Stability? |url=http://www.guerrillaexplorer.com/2011/11/island-of-stability.html |accessdate=2012-07-24}}</ref><!-- 1969? --> The hypothesis is based upon the ], which implies that the ] is built up in "shells" in a manner similar to the structure of the much larger electron shells in atoms. In both cases, shells are just groups of quantum ]s that are relatively close to each other. Energy levels from quantum states in two different shells will be separated by a relatively large energy gap, so when the number of ]s and ]s completely fills the ]s of a given shell in the nucleus, the ] per nucleon will reach a local maximum and thus that particular configuration will have a longer lifetime than nearby nuclides that do not possess filled shells.<ref>{{cite web |last=Nave |first=R. |date=|title=Shell Model of Nucleus |work=] |publisher=Department of Physics and Astronomy, ] |url=http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/shell.html |accessdate=22 January 2007 }}</ref> | ||
Revision as of 08:31, 12 August 2017
For the speech by Jimmy Carter, see Island of Stability (speech).
| Nuclear physics |
|---|
 |
| Models of the nucleus |
Nuclides' classification
|
| Nuclear stability |
| Radioactive decay |
| Nuclear fission |
| Capturing processes |
| High-energy processes |
|
Nucleosynthesis and nuclear astrophysics
|
| High-energy nuclear physics |
| Scientists |
In nuclear physics, the island of stability is the prediction that a set of heavy nuclides with a near magic number of protons and neutrons will temporarily reverse the trend of decreasing stability in elements heavier than uranium. Although predictions of the exact location differ somewhat, Klaus Blaum expects the island of stability to occur in the atomic mass region near the nuclide
120Ubn
. Estimates about the amount of stability on the island are usually around a half-life of minutes or days, with some predictions expecting half-lives of millions of years.
Although the nuclear shell model has existed since the 1960s, the existence of such superheavy, relatively stable nuclides has not been demonstrated. Like the rest of the superheavy elements, the nuclides on the island of stability have never been found in nature, and so must be created artificially in a nuclear reaction to be studied. However, scientists have not found a way to carry out such a reaction.
With an nuclide graph of protons and neutrons with the third dimension of height being the binding energy, the stability region can be visualized as a valley instead of an island.
Theory and origin
The possibility of an "island of stability" was first proposed by Glenn T. Seaborg in the late 1960s. The hypothesis is based upon the nuclear shell model, which implies that the atomic nucleus is built up in "shells" in a manner similar to the structure of the much larger electron shells in atoms. In both cases, shells are just groups of quantum energy levels that are relatively close to each other. Energy levels from quantum states in two different shells will be separated by a relatively large energy gap, so when the number of neutrons and protons completely fills the energy levels of a given shell in the nucleus, the binding energy per nucleon will reach a local maximum and thus that particular configuration will have a longer lifetime than nearby nuclides that do not possess filled shells.
Magic numbers
A filled shell would have "magic numbers" of neutrons and protons. This idea of a magic number derives from the counterpart of electron shells. The magic number for electron shells is 8. This completes the shell and makes it stable. Similarly, it is believed that there are complete shells in the nucleus that stabilize the nucleus. One possible magic number of neutrons for spherical nuclei is 184, and some possible matching proton numbers are 114, 120 and 126 – which would mean that the most stable spherical nuclides would be flerovium-298, unbinilium-304 and unbihexium-310. Of particular note is Fl, which would be "doubly magic" (both its proton number of 114 and neutron number of 184 are thought to be magic) and thus the most likely to have a very long half-life. (The next lighter doubly magic spherical nucleus is lead-208, the heaviest known stable nucleus and most stable heavy metal.)
Deformed nuclei
Studies from the early 1990s, and previous to that time, have shown that superheavy elements do not have perfectly spherical nuclei. A shell is considered stable when it is in a spherical form. A change in the shape of the nucleus changes the position of neutrons and protons in the shell, thus skewing the numbers. Recent research indicates that large nuclei are deformed, causing magic numbers to shift. A nucleus can have a magic number of neutrons or a magic number of protons. When the nucleus has magic numbers of both protons and neutrons, it can be said to be doubly magic. Hassium-270 is now believed to be a doubly magic deformed nucleus, with deformed magic numbers 108 and 162. It has a half-life of 3.6 seconds.
Experiments
Whilst elements with atomic numbers expected for the island of stability have been produced, the total nucleon count of these nuclides has been too low. These synthesised nuclides have contained too few neutrons to reach the supposed stable region. It is possible that these elements possess unusual chemical properties and, if they have isotopes with adequate lifespans, would be available for various practical applications (such as particle accelerator targets and as neutron sources as well). In particular, the very small critical masses of transplutonic elements (possibly as small as grams) implies that if stable elements could be found, they would enable small and compact nuclear bombs either directly or by serving as primaries to help ignite fission/fusion secondaries; this possibility motivated much of the early research in the 1960s and multiple nuclear tests by the United States (including Operation Plowshare) and the Soviet Union aimed at producing such elements.
Half-lives of the highest-numbered elements
All elements with an atomic number above 82 (lead) are unstable, and the "stability" (half-life of the longest-lived known isotope) of elements generally decreases with rising atomic numbers from the relatively stable uranium (92) upwards to the heaviest known element, oganesson (118). The longest-lived observed isotopes of each of the heaviest elements are shown in the following table.
(Note that for elements 108–118, the longest-lived known isotope is always the heaviest discovered thus far. This makes it seem likely that there are longer-lived undiscovered isotopes among the even heavier ones.)
For comparison, the shortest-lived element with atomic number below 100 is francium (element 87) with a half-life of 22 minutes.
The half-lives of nuclei in the island of stability itself are unknown since none of the nuclides that would be "on the island" have been observed. Many physicists think they are relatively short, on the order of minutes or days. Some theoretical calculations indicate that their half-lives may be long, on the order of 10 years.
The alpha-decay half-lives of 1700 nuclei with 100 ≤ Z ≤ 130 have been calculated in a quantum tunneling model with both experimental and theoretical alpha-decay Q-values. The theoretical calculations are in good agreement with the available experimental data.
A possible stronger decay mode for the heaviest superheavies was shown to be cluster decay by Dorin N. Poenaru, R.A. Gherghescu, and Walter Greiner.

Islands of relative stability
| Actinides and fission products by half-life | ||||||||
|---|---|---|---|---|---|---|---|---|
| Actinides by decay chain | Half-life range (a) |
Fission products of U by yield | ||||||
| 4n | 4n + 1 | 4n + 2 | 4n + 3 | 4.5–7% | 0.04–1.25% | <0.001% | ||
| Ra | 4–6 a | Eu | ||||||
| Bk | > 9 a | |||||||
| Cm | Pu | Cf | Ac | 10–29 a | Sr | Kr | Cd | |
| U | Pu | Cm | 29–97 a | Cs | Sm | Sn | ||
| Cf | Am | 141–351 a |
No fission products have a half-life | |||||
| Am | Cf | 430–900 a | ||||||
| Ra | Bk | 1.3–1.6 ka | ||||||
| Pu | Th | Cm | Am | 4.7–7.4 ka | ||||
| Cm | Cm | 8.3–8.5 ka | ||||||
| Pu | 24.1 ka | |||||||
| Th | Pa | 32–76 ka | ||||||
| Np | U | U | 150–250 ka | Tc | Sn | |||
| Cm | Pu | 327–375 ka | Se | |||||
| 1.33 Ma | Cs | |||||||
| Np | 1.61–6.5 Ma | Zr | Pd | |||||
| U | Cm | 15–24 Ma | I | |||||
| Pu | 80 Ma |
... nor beyond 15.7 Ma | ||||||
| Th | U | U | 0.7–14.1 Ga | |||||
| ||||||||
| 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | |||||||||||||||||||
| 154 |
|
Cm | Cf | 154 | ||||||||||||||||||||||||||
| 153 | Cf | Es | 153 | |||||||||||||||||||||||||||
| 152 | Cm | Cf | 152 | |||||||||||||||||||||||||||
| 151 | Cm | Bk | Cf | 151 | ||||||||||||||||||||||||||
| 150 | Pu | Cm | Bk | 150 | ||||||||||||||||||||||||||
| 149 | Cm | 149 | ||||||||||||||||||||||||||||
| 148 | Pu | Am | Cm | 148 | ||||||||||||||||||||||||||
| 147 | Pu | ⁂ | Cm | 147 | ||||||||||||||||||||||||||
| 146 | U | Pu | Am | 146 | ||||||||||||||||||||||||||
| 145 | Pu | 145 | ||||||||||||||||||||||||||||
| 144 | U | Np | Pu | 144 | ||||||||||||||||||||||||||
| 143 | U | Np | 143 | |||||||||||||||||||||||||||
| 142 | Th | U | Np | Pu | 142 | |||||||||||||||||||||||||
| 141 | U | 141 | ||||||||||||||||||||||||||||
| 140 | Ra | Th | Pa | U |
|
140 | ||||||||||||||||||||||||
| 139 | Th | 139 | ||||||||||||||||||||||||||||
| 138 | Ra | Ac | Th | 138 | ||||||||||||||||||||||||||
| 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | |||||||||||||||||||
| Only nuclides with a half-life of at least one year are shown on this table. | ||||||||||||||||||||||||||||||
Th (thorium),
U and
U (uranium) are the only naturally occurring nuclides beyond bismuth that are relatively stable over the current lifespan of the universe. Even bismuth was found to be slightly unstable in 2003, with an α-emission half-life of 1.9×10 years for
Bi. All elements beyond bismuth have relatively or very unstable isotopes: astatine, radon, and francium are extremely short-lived (and only have half-lives longer than isotopes of the heaviest elements found so far). Even thorium, with the largest known half-life in this region (1.4×10 years for
Th), is still about a billion times shorter than
Bi, so the main periodic table ends there.
By geographical analogy, bismuth is the shore edge of a continent. A continental shelf continues though, with shallows beginning at radium (see 'map' at right) that rapidly drop off again after californium. Significant islands appear at thorium and uranium, and with minor ones (i.e. neptunium, plutonium and curium) form an archipelago. All of this is surrounded by a "sea of instability". As can be seen from the table, there is a significantly large gap between the half-lives of the longest-lived actinide nuclides (the primordial Th, U, and U, separated sharply from the long-lived Pu, U, Cm, and Np) and those of the others.
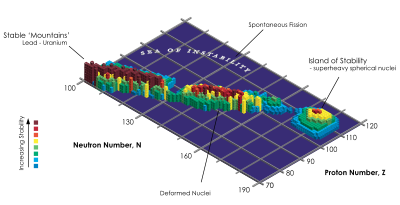
Current theoretical investigation indicates that in the region Z = 106–108 and N ≈ 160–164, a small ‘island/peninsula’ might be stable with respect to fission and beta decay, such superheavy nuclei undergoing only alpha decay. Also,
Fl is not the center of the magic island as predicted earlier. On the contrary, the nucleus with Z = 110, N = 183 (Ds) appears to be near the center of a possible 'magic island' (Z = 104–116, N ≈ 176–186). In the N ≈ 162 region the beta-stable, fission survived
Sg is predicted to have alpha-decay half-life ≈3.2 hours that is greater than that (≈28 s) of the deformed doubly magic
Hs. The superheavy nucleus
Sg has not been produced in the laboratory as yet (2009). For superheavy nuclei with Z > 116 and N ≈ 184 the alpha-decay half-lives are predicted to be less than one second. The nuclei with Z = 120, 124, 126 and N = 184 (Ubn, Ubq, and Ubh) are predicted to form spherical doubly magic nuclei and be stable with respect to fission. Calculations in a quantum tunneling model show that such superheavy nuclei would undergo alpha decay within microseconds or less.
Synthesis problems
The manufacture of nuclei on the island of stability proves to be very difficult because the nuclei available as starting materials do not deliver the necessary sum of neutrons. For the synthesis of isotope 298 of flerovium, one could use an isotope of plutonium and one of calcium that together have a sum of at least 298 nucleons; for example, calcium-50 and plutonium-248. These and heavier nuclides are not available in measurable quantities, making production virtually impossible with current methods. The same problem exists for the other possible combinations of nuclides needed to generate elements on the island using target-projectile methods. It may be possible to generate the isotope 298 of flerovium, if the multi-nucleon transfer reactions would work in low-energy collisions of actinide nuclei. One of these reactions may be:
Cm
+
U
→
Fl
+
W
+ 2
0n
Hypothetical second island
At the 235th national meeting of the American Chemical Society in 2008, the idea of a second island of stability was presented by Yuri Oganessian. This new island would be centered on element 164 (unhexquadium), especially the isotope Uhq, with a stability similar to that of flerovium. It is thought that to be able to synthesize these elements, a new, stronger particle accelerator would be needed.
See also
References
- "Superheavy, and yet stable". Max-Planck-Gesellschaft. 23 August 2012. Retrieved 23 June 2013.
We expect at around element 120," says Blaum, "and to be more precise, in a nucleus with around 180 neutrons.
- ^ "Superheavy Element 114 Confirmed: A Stepping Stone to the Island of Stability". Berkeley Lab. 24 September 2009. Retrieved 25 October 2016.
- CEA Sciences. The Valley of Stability (video) - a virtual "flight" through 3D representation of the nuclide chart. YouTube. Event occurs at 3:12.
- "The Island of Stability?". Retrieved 2012-07-24.
- Nave, R. "Shell Model of Nucleus". HyperPhysics. Department of Physics and Astronomy, Georgia State University. Retrieved 22 January 2007.
- "Structure of Odd-N Superheavy Elements". 1999.
{{cite journal}}: Cite journal requires|journal=(help) - Dvořák, J. (2007). Decay properties of nuclei close to Z = 108 and N = 162 (PhD thesis). Technische Universität München.
- Dvorak, J. (2006). "Doubly Magic Nucleus
108Hs
162". Physical Review Letters. 97 (24): 242501. Bibcode:2006PhRvL..97x2501D. doi:10.1103/PhysRevLett.97.242501. PMID 17280272.{{cite journal}}: Unknown parameter|displayauthors=ignored (|display-authors=suggested) (help) - Gsponer, A.; Hurni, J.-P. (2009). Fourth Generation Nuclear Weapons: The physical principles of thermonuclear explosives, inertial confinement fusion, and the quest for fourth generation nuclear weapons (3rd printing of the 7th ed.). pp. 129–133.
- Emsley, J. (2001). Nature's Building Blocks. Oxford University Press. pp. 143−144, 458. ISBN 0-19-850340-7.
- Khuyagbaatar, J. (2014). "Ca+Bk Fusion Reaction Leading to Element Z = 117: Long-Lived α-Decaying Db and Discovery of Lr". Physical Review Letters. 112: 172501. Bibcode:2014PhRvL.112q2501K. doi:10.1103/PhysRevLett.112.172501.
- Witze, A. (6 April 2010). "Superheavy element 117 makes debut". ScienceNews. Retrieved 2010-04-06.
- Oganessian, Y. (2012). "Nuclei in the "Island of Stability" of Superheavy Elements". Journal of Physics: Conference Series. 337 (1): 012005. Bibcode:2012JPhCS.337a2005O. doi:10.1088/1742-6596/337/1/012005.
- Chowdhury, P. R.; Samanta, C.; Basu, D. N. (2006). "α decay half-lives of new superheavy elements". Physical Review C. 73: 014612. arXiv:nucl-th/0507054. Bibcode:2006PhRvC..73a4612C. doi:10.1103/PhysRevC.73.014612.
- ^ Samanta, C.; Chowdhury, P. R.; Basu, D. N. (2007). "Predictions of alpha decay half lives of heavy and superheavy elements". Nuclear Physics A. 789: 142–154. arXiv:nucl-th/0703086. Bibcode:2007NuPhA.789..142S. doi:10.1016/j.nuclphysa.2007.04.001.
- ^ Chowdhury, P. R.; Samanta, C.; Basu, D. N. (2008). "Search for long lived heaviest nuclei beyond the valley of stability". Physical Review C. 77 (4): 044603. arXiv:0802.3837. Bibcode:2008PhRvC..77d4603C. doi:10.1103/PhysRevC.77.044603.
- ^ Chowdhury, P. R.; Samanta, C.; Basu, D. N. (2008). "Nuclear half-lives for α-radioactivity of elements with 100 ≤ Z ≤ 130". Atomic Data and Nuclear Data Tables. 94 (6): 781–806. arXiv:0802.4161. Bibcode:2008ADNDT..94..781C. doi:10.1016/j.adt.2008.01.003.
- Chowdhury, P. R.; Basu, D. N.; Samanta, C. (2007). "α decay chains from element 113". Physical Review C. 75 (4): 047306. arXiv:0704.3927. Bibcode:2007PhRvC..75d7306C. doi:10.1103/PhysRevC.75.047306.
- Samanta, C.; Basu, D. N.; Chowdhury, P. R. (2007). "Quantum tunneling in 112 and its alpha-decay chain". Journal of the Physical Society of Japan. 76 (12): 124201. arXiv:0708.4355. Bibcode:2007JPSJ...76l4201S. doi:10.1143/JPSJ.76.124201.
- Poenaru, D. N.; Gherghescu, R. A.; Greiner, W. (2011). "Heavy-Particle Radioactivity of Superheavy Nuclei". Physical Review Letters. 107 (6): 062503. arXiv:1106.3271. Bibcode:2011PhRvL.107f2503P. doi:10.1103/PhysRevLett.107.062503. PMID 21902317.
- Plus radium (element 88). While actually a sub-actinide, it immediately precedes actinium (89) and follows a three-element gap of instability after polonium (84) where no nuclides have half-lives of at least four years (the longest-lived nuclide in the gap is radon-222 with a half life of less than four days). Radium's longest lived isotope, at 1,600 years, thus merits the element's inclusion here.
- Specifically from thermal neutron fission of uranium-235, e.g. in a typical nuclear reactor.
- Milsted, J.; Friedman, A. M.; Stevens, C. M. (1965). "The alpha half-life of berkelium-247; a new long-lived isomer of berkelium-248". Nuclear Physics. 71 (2): 299. Bibcode:1965NucPh..71..299M. doi:10.1016/0029-5582(65)90719-4.
"The isotopic analyses disclosed a species of mass 248 in constant abundance in three samples analysed over a period of about 10 months. This was ascribed to an isomer of Bk with a half-life greater than 9 . No growth of Cf was detected, and a lower limit for the β half-life can be set at about 10 . No alpha activity attributable to the new isomer has been detected; the alpha half-life is probably greater than 300 ." - This is the heaviest nuclide with a half-life of at least four years before the "sea of instability".
- Excluding those "classically stable" nuclides with half-lives significantly in excess of Th; e.g., while Cd has a half-life of only fourteen years, that of Cd is eight quadrillion years.
- Note graphic: Known and predicted regions of nuclear stability, surrounded by a "sea" of instability. cf. the Chart of Nuclides by half-life.
- Nilsson, S. G.; et al. (1969). "On the nuclear structure and stability of heavy and superheavy elements". Nuclear Physics A. 131 (1): 1–66. Bibcode:1969NuPhA.131....1N. doi:10.1016/0375-9474(69)90809-4.
- Dvorak, J.; et al. (2006). "Doubly Magic Nucleus
108Hs
162". Physical Review Letters. 97 (24). Bibcode:2006PhRvL..97x2501D. doi:10.1103/PhysRevLett.97.242501. PMID 17280272. - Ćwiok, S.; Heenen, P.-H.; Nazarewicz, W. (2005). "Shape coexistence and triaxiality in the superheavy nuclei" (PDF). Nature. 433 (7027): 705–709. Bibcode:2005Natur.433..705C. doi:10.1038/nature03336. PMID 15716943.
- Zagrebaev, V.; Greiner, W. (2008). "Synthesis of superheavy nuclei: A search for new production reactions". Physical Review C. 78 (3). arXiv:0807.2537. Bibcode:2008PhRvC..78c4610Z. doi:10.1103/PhysRevC.78.034610.
- Grumann, J.; Mosel, U.; Fink, B.; Greiner, W. (1969). "Investigation of the stability of superheavy nuclei around Z = 114 and Z = 164". Zeitschrift für Physik. 228: 371–386. Bibcode:1969ZPhy..228..371G. doi:10.1007/BF01406719.
- "Nuclear scientists eye future landfall on a second 'island of stability'". Eurekalert.org. 2008-04-06. Retrieved 2014-05-02.
External links
- Six new isotopes of the superheavy elements discovered (Oct 26 2010, Physorg news. Inc chart of heavy nuclides)
- Exploring the island of superheavy elements (April 2010, re decay of 117; with chart)
- Hunting the biggest atoms in the universe (July 23, 2008; claimed finding natural atoms of 122 protons and 170 neutrons)
- The hunt for superheavy elements (April 7, 2008; prediction of seaborgium-290 half-life of 10 years.)
- Here be stability (Nature Aug 2006 with JINR diagram of heavy nuclides and predicted IoS)
- Superheavy elements (Jul 2004 Yuri Oganessian of JINR )
- Uut and Uup Add Their Atomic Mass to Periodic Table (Feb 2004)
- Can superheavy elements (such as Z = 116 or 118) be formed in a supernova? Can we observe them? 2004 – "maybe"
- Second postcard from the island of stability (Oct 2001) nuclides with 116 protons and mass 292
- The synthesis of spherical superheavy nuclei in Ca induced reactions Reports the 1999 synthesis of Z = 114, N + Z = 287.
- New elements discovered and the island of stability sighted (Aug 1999; includes report on article later retracted)
- First postcard from the island of nuclear stability (1999; first few Z = 114 atoms)
- NOVA: Island of Stability (2006. 13m TV segment, with transcript)
- New York Times editorial by Oliver Sacks regarding the Island of Stability theory (Feb 2004 re 113 and 115)
- Tendency equation and curve of stable nuclides