| Revision as of 17:07, 2 March 2018 edit101.15.112.240 (talk) →Some properties← Previous edit | Revision as of 17:39, 3 March 2018 edit undo49.216.50.153 (talk) →Some propertiesTag: repeating charactersNext edit → | ||
| Line 1,065: | Line 1,065: | ||
| If ''p'' is a safe prime other than 5, 7 and Ɛ, then the ] of 1/''p'' is (''p''-1)/2. (this is not true for all primes ends with Ɛ (other than Ɛ itself), the first counterexample is ''p'' = 2ƐƐ, where the period length of 1/''p'' is only 37) | If ''p'' is a safe prime other than 5, 7 and Ɛ, then the ] of 1/''p'' is (''p''-1)/2. (this is not true for all primes ends with Ɛ (other than Ɛ itself), the first counterexample is ''p'' = 2ƐƐ, where the period length of 1/''p'' is only 37) | ||
| By ], if ''p'' is a prime other than 2, 3 and Ɛ, then ''p'' divides the ] with length ''p''−1. (The converse is not true, the first counterexample is 55, which is composite (equals 5×11) but divides the repunit with length 54) Thus, we can prove that every positive integer coprime to 10 has a repunit multiple, and every positive integer has a multiple uses only 0's and 1's. | By ], if ''p'' is a prime other than 2, 3 and Ɛ, then ''p'' divides the ] with length ''p''−1. (The converse is not true, the first counterexample is 55, which is composite (equals 5×11) but divides the repunit with length 54) Thus, we can prove that every positive integer coprime to 10 has a repunit multiple, and every positive integer has a multiple uses only 0's and 1's. (the smallest multiple of ''n'' uses only 0's and 1's are 1, 10, 10, 10, 101, 10, 1001, 100, 100, 1010, 11111111111, 10, 11, 10010, 1010, 100, ...) | ||
| The only two ]s < 10<sup>10</sup> are 1685 and 5Ɛ685, note that both of the numbers end with 685, and it is conjectured that all base 10 Wieferich primes end with 685. | The only two ]s < 10<sup>10</sup> are 1685 and 5Ɛ685, note that both of the numbers end with 685, and it is conjectured that all base 10 Wieferich primes end with 685. | ||
Revision as of 17:39, 3 March 2018
Not to be confused with Dewey Decimal Classification or duodecimo. This article contains special characters. Without proper rendering support, you may see question marks, boxes, or other symbols.| Part of a series on | ||||
| Numeral systems | ||||
|---|---|---|---|---|
Place-value notation
|
||||
Sign-value notation
|
||||
| List of numeral systems | ||||
The duodecimal system (also known as base 12 or dozenal) is a positional notation numeral system using twelve as its base. In this system, the number ten may be written by a rotated "2" (2) and the number eleven by a rotated "3" (3). This notation was introduced by Sir Isaac Pitman. These digit forms are available as Unicode characters on computerized systems since June 2015 as ↊ (Code point 218A) and ↋ (Code point 218B), respectively. Other notations use "A", "T", or "X" for ten and "B" or "E" for eleven. The number twelve (that is, the number written as "12" in the base ten numerical system) is instead written as "10" in duodecimal (meaning "1 dozen and 0 units", instead of "1 ten and 0 units"), whereas the digit string "12" means "1 dozen and 2 units" (i.e. the same number that in decimal is written as "14"). Similarly, in duodecimal "100" means "1 gross", "1000" means "1 great gross", and "0.1" means "1 twelfth" (instead of their decimal meanings "1 hundred", "1 thousand", and "1 tenth").
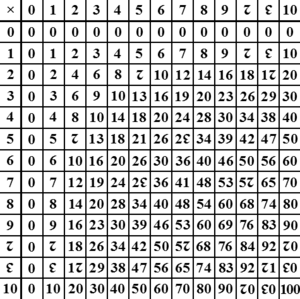
The number twelve, a superior highly composite number, is the smallest number with four non-trivial factors (2, 3, 4, 6), and the smallest to include as factors all four numbers (1 to 4) within the subitizing range. As a result of this increased factorability of the radix and its divisibility by a wide range of the most elemental numbers (whereas ten has only two non-trivial factors: 2 and 5, and not 3, 4, or 6), duodecimal representations fit more easily than decimal ones into many common patterns, as evidenced by the higher regularity observable in the duodecimal multiplication table. As a result, duodecimal has been described as the optimal number system. Of its factors, 2 and 3 are prime, which means the reciprocals of all 3-smooth numbers (such as 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, ...) have a terminating representation in duodecimal. In particular, the five most elementary fractions (+1⁄2, +1⁄3, +2⁄3, +1⁄4 and +3⁄4) all have a short terminating representation in duodecimal (0.6, 0.4, 0.8, 0.3 and 0.9, respectively), and twelve is the smallest radix with this feature (because it is the least common multiple of 3 and 4). This all makes it a more convenient number system for computing fractions than most other number systems in common use, such as the decimal, vigesimal, binary, octal and hexadecimal systems. Although the trigesimal and sexagesimal systems (where the reciprocals of all 5-smooth numbers terminate) do even better in this respect, this is at the cost of unwieldy multiplication tables and a much larger number of symbols to memorize.
Origin
Languages using duodecimal number systems are uncommon. Languages in the Nigerian Middle Belt such as Janji, Gbiri-Niragu (Gure-Kahugu), Piti, and the Nimbia dialect of Gwandara; the Chepang language of Nepal and the Mahl language of Minicoy Island in India are known to use duodecimal numerals.
Germanic languages have special words for 11 and 12, such as eleven and twelve in English. However, they are considered to come from Proto-Germanic *ainlif and *twalif (respectively one left and two left), both of which were decimal.
Historically, units of time in many civilizations are duodecimal. There are twelve signs of the zodiac, twelve months in a year, and the Babylonians had twelve hours in a day (although at some point this was changed to 24). Traditional Chinese calendars, clocks, and compasses are based on the twelve Earthly Branches. There are 12 inches in an imperial foot, 12 troy ounces in a troy pound, 12 old British pence in a shilling, 24 (12×2) hours in a day, and many other items counted by the dozen, gross (144, square of 12) or great gross (1728, cube of 12). The Romans used a fraction system based on 12, including the uncia which became both the English words ounce and inch. Pre-decimalisation, Ireland and the United Kingdom used a mixed duodecimal-vigesimal currency system (12 pence = 1 shilling, 20 shillings or 240 pence to the pound sterling or Irish pound), and Charlemagne established a monetary system that also had a mixed base of twelve and twenty, the remnants of which persist in many places.
| Table of units from a base of 12 | |||||
|---|---|---|---|---|---|
| Relative value |
French unit of length |
English unit of length |
English unit of weight |
Roman unit of weight |
English unit of mass |
| 12 | pied | foot | pound | libra | |
| 12 | pouce | inch | ounce | uncia | slinch |
| 12 | ligne | line | 2 scruples | 2 scrupulum | slug |
| 12 | point | point | seed | siliqua | |
The importance of 12 has been attributed to the number of lunar cycles in a year, and also to the fact that humans have 12 finger bones (phalanges) on one hand (three on each of four fingers). It is possible to count to 12 with the thumb acting as a pointer, touching each finger bone in turn. A traditional finger counting system still in use in many regions of Asia works in this way, and could help to explain the occurrence of numeral systems based on 12 and 60 besides those based on 10, 20 and 5. In this system, the one (usually right) hand counts repeatedly to 12, displaying the number of iterations on the other (usually left), until five dozens, i. e. the 60, are full.
Notations and pronunciations
Transdecimal symbols
In a duodecimal place system twelve is written as 10, but there are numerous proposals for how to write ten and eleven. The simplified notations use only basic and easy to access letters such as T and E (for ten and eleven), X and Z, t and e, d and k, others use A and B or a and b as in the hexadecimal system. Some employ Greek letters such as δ (standing for Greek δέκα 'ten') and ε (for Greek ένδεκα 'eleven'), or τ and ε. Frank Emerson Andrews, an early American advocate for duodecimal, suggested and used in his book New Numbers an X (from the Roman numeral for ten) and a script E (ℰ, U+2130).
The Dozenal Society of Great Britain proposes a rotated digit two 2 (↊, U+218A) for ten and a reversed or rotated digit three 3 (↋, U+218B) for eleven. This notation was introduced by Sir Isaac Pitman.
Until 2015, the Dozenal Society of America (DSA) used ![]() and
and ![]() , the symbols devised by William Addison Dwiggins. After the Pitman digits (↊, U+218A and ↋, U+218B) were added to Unicode in 2015, the DSA took a vote and then began publishing content using the Pitman digits instead. They still use the letters X and E as the equivalent in ASCII text.
, the symbols devised by William Addison Dwiggins. After the Pitman digits (↊, U+218A and ↋, U+218B) were added to Unicode in 2015, the DSA took a vote and then began publishing content using the Pitman digits instead. They still use the letters X and E as the equivalent in ASCII text.
Other proposals are more creative or aesthetic, for example, Edna Kramer in her 1951 book The Main Stream of Mathematics used a six-pointed asterisk (sextile) ⚹ for ten and a hash (or octothorpe) # for eleven. The symbols were chosen because they are available in typewriters and already present in telephone dials. This notation was used in publications of the Dozenal Society of America in the period 1974–2008. Many don't use any of the Hindu-Arabic symbols, under the principle of "separate identity."
Base notation
There are also varying proposals of how to distinguish a duodecimal number from a decimal one, or one in a different base. They include italicizing duodecimal numbers ( 54 = 64 ), adding a "Humphrey point" (a semicolon ";" instead of a decimal point "." ) to duodecimal numbers ( 54; = 64. ) ( 54;0 = 64.0 ), or some combination of the two. More also add extra marking to one or more bases. Others use subscript or affixed labels to indicate the base, allowing for more than decimal and duodecimal to be represented:
| Common Base | Abb. | Letter | Cardinal | Decimal | Duodecimal |
|---|---|---|---|---|---|
| binary | bin | b | two | 2 | 2 |
| octal | oct | o | eight | 8 | 8 |
| decimal | dec | d | ten | 10 | ↊ |
| dozenal (duodecimal) | doz | z | twelve | 12 | 10 |
| hexadecimal | hex | x | sixteen | 16 | 14 |
This allows one to write "54z = 64d," "54twelve = 64ten" or "doz 54 = dec 64." In programming, binary, octal, and hexadecimal often use a similar scheme: a binary number starts with 0b, octal with 0o, and hexadecimal with 0x.
Pronunciation
The Dozenal Society of America suggests the pronunciation of ten and eleven as "dek" and "el", each order has its own name and the prefix e- is added for fractions. The symbol corresponding to the decimal point or decimal comma, separating the whole number part from the fractional part, is the semicolon ";". The overall system is:
| Duodecimal | Name | Decimal | Duodecimal fraction | Name |
|---|---|---|---|---|
| 1 | one | 1 | ||
| 10 | do | 12 | 0;1 | edo |
| 100 | gro | 144 | 0;01 | egro |
| 1,000 | mo | 1,728 | 0;001 | emo |
| 10,000 | do-mo | 20,736 | 0;000,1 | edo-mo |
| 100,000 | gro-mo | 248,832 | 0;000,01 | egro-mo |
| 1,000,000 | bi-mo | 2,985,984 | 0;000,001 | ebi-mo |
| 1,000,000,000 | tri-mo | 5,159,780,352 | 0;000,000,001 | etri-mo |
Multiple digits in this are pronounced differently. 12 is "one do two", 30 is "three do", 100 is "one gro", BA9 (ET9) is "el gro dek do nine", B8,65A,300 (E8,65T,300) is "el do eight bi-mo, six gro five do dek mo, three gro", and so on.
Advocacy and "dozenalism"
The case for the duodecimal system was put forth at length in F. Emerson Andrews' 1935 book New Numbers: How Acceptance of a Duodecimal Base Would Simplify Mathematics. Emerson noted that, due to the prevalence of factors of twelve in many traditional units of weight and measure, many of the computational advantages claimed for the metric system could be realized either by the adoption of ten-based weights and measure or by the adoption of the duodecimal number system.
The Dozenal Society of America and the Dozenal Society of Great Britain promote widespread adoption of the base-twelve system. They use the word "dozenal" instead of "duodecimal" because the latter comes from Latin roots that express twelve in base-ten terminology.
It should be noted that the etymology of 'dozenal' is itself also an expression based on base-ten terminology since 'dozen' is a direct derivation of the French word 'douzaine' which is a derivative of the French word for twelve, douze which is related to the old French word 'doze' from Latin 'duodecim'. It has been suggested by some members of the Dozenal Society of America and Duodecimal Society of Great Britain that a more apt word would be 'uncial'. This is a derivation of the Latin word 'uncia' which means one-twelfth and is the base-twelve analogue of the Latin word 'decima' meaning one-tenth. In the same manner as decimal comes from the Latin word for one-tenth decima, (Latin for ten was decem), the direct analogue for a base-twelve system is uncial. An early use of this word can be found in Vol 1 Issue 2 of The Duodecimal Bulletin of the DSA dated June 1945 in which a submission on page 9 by a Pvt William S. Crosby titled "The Uncial Jottings of a Harried Infantryman", he includes the same argument for the word 'uncial'. Although not accepted by either of these two 'Uncial' societies, the use is beginning to grow.
The renowned mathematician and mental calculator Alexander Craig Aitken was an outspoken advocate of the advantages and superiority of duodecimal over decimal:
The duodecimal tables are easy to master, easier than the decimal ones; and in elementary teaching they would be so much more interesting, since young children would find more fascinating things to do with twelve rods or blocks than with ten. Anyone having these tables at command will do these calculations more than one-and-a-half times as fast in the duodecimal scale as in the decimal. This is my experience; I am certain that even more so it would be the experience of others.
— A. C. Aitken, "Twelves and Tens", in The Listener, January 25, 1962
But the final quantitative advantage, in my own experience, is this: in varied and extensive calculations of an ordinary and not unduly complicated kind, carried out over many years, I come to the conclusion that the efficiency of the decimal system might be rated at about 65 or less, if we assign 100 to the duodecimal.
— A. C. Aitken, The Case Against Decimalisation (Edinburgh / London: Oliver & Boyd, 1962)
In Jorge Luis Borges' short story Tlön, Uqbar, Orbis Tertius Herbert Ashe, a melancholy English engineer, working for the Southern Argentine Railway company, is converting a duodecimal number system to a hexadecimal system. He leaves behind on his death in 1937 a manuscript Orbis Tertius that posthumously identifies him as one of the anonymous authors of the encyclopaedia of Tlön.
In Leo Frankowski's Conrad Stargard novels, Conrad introduces a duodecimal system of arithmetic at the suggestion of a merchant, who is accustomed to buying and selling goods in dozens and grosses, rather than tens or hundreds. He then invents an entire system of weights and measures in base twelve, including a clock with twelve hours in a day, rather than twenty-four hours.
In Lee Carroll's Kryon: Alchemy of the Human Spirit, a chapter is dedicated to the advantages of the duodecimal system. The duodecimal system is supposedly suggested by Kryon (a fictional entity believed in by New Age circles) for all-round use, aiming at better and more natural representation of nature of the Universe through mathematics. An individual article "Mathematica" by James D. Watt (included in the above publication) exposes a few of the unusual symmetry connections between the duodecimal system and the golden ratio, as well as provides numerous number symmetry-based arguments for the universal nature of the base-12 number system.
In "Little Twelvetoes", American television series Schoolhouse Rock! portrayed an alien child using base-twelve arithmetic, using "dek", "el" and "doh" as names for ten, eleven and twelve, and Andrews' script-X and script-E for the digit symbols.
In computing
In March 2013, a proposal was submitted to include the digit forms for ten and eleven propagated by the Dozenal Societies of Great Britain and America in the Unicode Standard. Of these, the British forms were accepted for encoding as characters at code points U+218A turned digit two (↊) and U+218B turned digit three (↋) They have been included in the Unicode 8.0 release in June 2015.
Unicode points U+218C and U+218D seem to be reserved for the Dwiggins digits (stylized X and E).
Few fonts support these new characters, but Abibas, EB Garamond, Everson Mono, Squarish Sans CT, and Symbola do.
Also, the turned digits two and three are available in LaTeX as \textturntwo and \textturnthree.
Duodecimal clock
- Dozenal Clock by Joshua Harkey
- Dozenal Clock with four hands and a digital display, in several variants, by Paul Rapoport
Duodecimal metric systems
Systems of measurement proposed by dozenalists include:
- Tom Pendlebury's TGM system
- Takashi Suga's Universal Unit System
Comparison to other numeral systems
The number 12 has six factors, which are 1, 2, 3, 4, 6, and 12, of which 2 and 3 are prime. The decimal system has only four factors, which are 1, 2, 5, and 10, of which 2 and 5 are prime. Vigesimal (base 20) adds two factors to those of ten, namely 4 and 20, but no additional prime factor. Although twenty has 6 factors, 2 of them prime, similarly to twelve, it is also a much larger base, and so the digit set and the multiplication table are much larger. Binary has only two factors, 1 and 2, the latter being prime. Hexadecimal (base 16) has five factors, adding 4, 8 and 16 to those of 2, but no additional prime. Trigesimal (base 30) is the smallest system that has three different prime factors (all of the three smallest primes: 2, 3 and 5) and it has eight factors in total (1, 2, 3, 5, 6, 10, 15, and 30). Sexagesimal—which the ancient Sumerians and Babylonians among others actually used—adds the four convenient factors 4, 12, 20, and 60 to this but no new prime factors. The smallest system that has four different prime factors is base 210 and the pattern follows the primorials. In all base systems, there are similarities to the representation of multiples of numbers which are one less than the base.
Conversion tables to and from decimal
To convert numbers between bases, one can use the general conversion algorithm (see the relevant section under positional notation). Alternatively, one can use digit-conversion tables. The ones provided below can be used to convert any duodecimal number between 0.01 and ƐƐƐ,ƐƐƐ.ƐƐ to decimal, or any decimal number between 0.01 and 999,999.99 to duodecimal. To use them, the given number must first be decomposed into a sum of numbers with only one significant digit each. For example:
- 123,456.78 = 100,000 + 20,000 + 3,000 + 400 + 50 + 6 + 0.7 + 0.08
This decomposition works the same no matter what base the number is expressed in. Just isolate each non-zero digit, padding them with as many zeros as necessary to preserve their respective place values. If the digits in the given number include zeroes (for example, 102,304.05), these are, of course, left out in the digit decomposition (102,304.05 = 100,000 + 2,000 + 300 + 4 + 0.05). Then the digit conversion tables can be used to obtain the equivalent value in the target base for each digit. If the given number is in duodecimal and the target base is decimal, we get:
- (duodecimal) 100,000 + 20,000 + 3,000 + 400 + 50 + 6 + 0.7 + 0.08 = (decimal) 248,832 + 41,472 + 5,184 + 576 + 60 + 6 + 0.583333333333... + 0.055555555555...
Now, because the summands are already converted to base ten, the usual decimal arithmetic is used to perform the addition and recompose the number, arriving at the conversion result:
Duodecimal -----> Decimal
100,000 = 248,832
20,000 = 41,472
3,000 = 5,184
400 = 576
50 = 60
+ 6 = + 6
0.7 = 0.583333333333...
0.08 = 0.055555555555...
--------------------------------------------
123,456.78 = 296,130.638888888888...
That is, (duodecimal) 123,456.78 equals (decimal) 296,130.638 ≈ 296,130.64
If the given number is in decimal and the target base is duodecimal, the method is basically same. Using the digit conversion tables:
(decimal) 100,000 + 20,000 + 3,000 + 400 + 50 + 6 + 0.7 + 0.08 = (duodecimal) 49,ᘔ54 + Ɛ,6ᘔ8 + 1,8ᘔ0 + 294 + 42 + 6 + 0.849724972497249724972497... + 0.0Ɛ62ᘔ68781Ɛ05915343ᘔ0Ɛ62...
However, in order to do this sum and recompose the number, now the addition tables for the duodecimal system have to be used, instead of the addition tables for decimal most people are already familiar with, because the summands are now in base twelve and so the arithmetic with them has to be in duodecimal as well. In decimal, 6 + 6 equals 12, but in duodecimal it equals 10; so, if using decimal arithmetic with duodecimal numbers one would arrive at an incorrect result. Doing the arithmetic properly in duodecimal, one gets the result:
Decimal -----> Duodecimal
100,000 = 49,ᘔ54
20,000 = Ɛ,6ᘔ8
3,000 = 1,8ᘔ0
400 = 294
50 = 42
+ 6 = + 6
0.7 = 0.849724972497249724972497...
0.08 = 0.0Ɛ62ᘔ68781Ɛ05915343ᘔ0Ɛ62...
--------------------------------------------------------
123,456.78 = 5Ɛ,540.943ᘔ0Ɛ62ᘔ68781Ɛ05915343ᘔ...
That is, (decimal) 123,456.78 equals (duodecimal) 5Ɛ,540.943ᘔ0Ɛ62ᘔ68781Ɛ059153... ≈ 5Ɛ,540.94
Duodecimal to decimal digit conversion
| Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1,000,000 | 2,985,984 | 100,000 | 248,832 | 10,000 | 20,736 | 1,000 | 1,728 | 100 | 144 | 10 | 12 | 1 | 1 | 0.1 | 0.083 | 0.01 | 0.00694 |
| 2,000,000 | 5,971,968 | 200,000 | 497,664 | 20,000 | 41,472 | 2,000 | 3,456 | 200 | 288 | 20 | 24 | 2 | 2 | 0.2 | 0.16 | 0.02 | 0.0138 |
| 3,000,000 | 8,957,952 | 300,000 | 746,496 | 30,000 | 62,208 | 3,000 | 5,184 | 300 | 432 | 30 | 36 | 3 | 3 | 0.3 | 0.25 | 0.03 | 0.02083 |
| 4,000,000 | 11,943,936 | 400,000 | 995,328 | 40,000 | 82,944 | 4,000 | 6,912 | 400 | 576 | 40 | 48 | 4 | 4 | 0.4 | 0.3 | 0.04 | 0.027 |
| 5,000,000 | 14,929,920 | 500,000 | 1,244,160 | 50,000 | 103,680 | 5,000 | 8,640 | 500 | 720 | 50 | 60 | 5 | 5 | 0.5 | 0.416 | 0.05 | 0.03472 |
| 6,000,000 | 17,915,904 | 600,000 | 1,492,992 | 60,000 | 124,416 | 6,000 | 10,368 | 600 | 864 | 60 | 72 | 6 | 6 | 0.6 | 0.5 | 0.06 | 0.0416 |
| 7,000,000 | 20,901,888 | 700,000 | 1,741,824 | 70,000 | 145,152 | 7,000 | 12,096 | 700 | 1,008 | 70 | 84 | 7 | 7 | 0.7 | 0.583 | 0.07 | 0.04861 |
| 8,000,000 | 23,887,872 | 800,000 | 1,990,656 | 80,000 | 165,888 | 8,000 | 13,824 | 800 | 1,152 | 80 | 96 | 8 | 8 | 0.8 | 0.6 | 0.08 | 0.05 |
| 9,000,000 | 26,873,856 | 900,000 | 2,239,488 | 90,000 | 186,624 | 9,000 | 15,552 | 900 | 1,296 | 90 | 108 | 9 | 9 | 0.9 | 0.75 | 0.09 | 0.0625 |
| ᘔ,000,000 | 29,859,840 | ᘔ00,000 | 2,488,320 | ᘔ0,000 | 207,360 | ᘔ,000 | 17,280 | ᘔ00 | 1,440 | ᘔ0 | 120 | ᘔ | 10 | 0.ᘔ | 0.83 | 0.0ᘔ | 0.0694 |
| Ɛ,000,000 | 32,845,824 | Ɛ00,000 | 2,737,152 | Ɛ0,000 | 228,096 | Ɛ,000 | 19,008 | Ɛ00 | 1,584 | Ɛ0 | 132 | Ɛ | 11 | 0.Ɛ | 0.916 | 0.0Ɛ | 0.07638 |
Decimal to duodecimal digit conversion
| Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100,000 | 49,ᘔ54 | 10,000 | 5,954 | 1,000 | 6Ɛ4 | 100 | 84 | 10 | ᘔ | 1 | 1 | 0.1 | 0.12497 | 0.01 | 0.015343ᘔ0Ɛ62ᘔ68781Ɛ059 |
| 200,000 | 97,8ᘔ8 | 20,000 | Ɛ,6ᘔ8 | 2,000 | 1,1ᘔ8 | 200 | 148 | 20 | 18 | 2 | 2 | 0.2 | 0.2497 | 0.02 | 0.02ᘔ68781Ɛ05915343ᘔ0Ɛ6 |
| 300,000 | 125,740 | 30,000 | 15,440 | 3,000 | 1,8ᘔ0 | 300 | 210 | 30 | 26 | 3 | 3 | 0.3 | 0.37249 | 0.03 | 0.043ᘔ0Ɛ62ᘔ68781Ɛ059153 |
| 400,000 | 173,594 | 40,000 | 1Ɛ,194 | 4,000 | 2,394 | 400 | 294 | 40 | 34 | 4 | 4 | 0.4 | 0.4972 | 0.04 | 0.05915343ᘔ0Ɛ62ᘔ68781Ɛ |
| 500,000 | 201,428 | 50,000 | 24,Ɛ28 | 5,000 | 2,ᘔ88 | 500 | 358 | 50 | 42 | 5 | 5 | 0.5 | 0.6 | 0.05 | 0.07249 |
| 600,000 | 24Ɛ,280 | 60,000 | 2ᘔ,880 | 6,000 | 3,580 | 600 | 420 | 60 | 50 | 6 | 6 | 0.6 | 0.7249 | 0.06 | 0.08781Ɛ05915343ᘔ0Ɛ62ᘔ6 |
| 700,000 | 299,114 | 70,000 | 34,614 | 7,000 | 4,074 | 700 | 4ᘔ4 | 70 | 5ᘔ | 7 | 7 | 0.7 | 0.84972 | 0.07 | 0.0ᘔ0Ɛ62ᘔ68781Ɛ05915343 |
| 800,000 | 326,Ɛ68 | 80,000 | 3ᘔ,368 | 8,000 | 4,768 | 800 | 568 | 80 | 68 | 8 | 8 | 0.8 | 0.9724 | 0.08 | 0.0Ɛ62ᘔ68781Ɛ05915343ᘔ |
| 900,000 | 374,ᘔ00 | 90,000 | 44,100 | 9,000 | 5,260 | 900 | 630 | 90 | 76 | 9 | 9 | 0.9 | 0.ᘔ9724 | 0.09 | 0.10Ɛ62ᘔ68781Ɛ05915343ᘔ |
Conversion of powers
| Exponent | b=2 | b=3 | b=4 | b=5 | b=6 | b=7 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | |
| b | 64 | 54 | 729 | 509 | 4,096 | 2,454 | 15,625 | 9,061 | 46,656 | 23,000 | 117,649 | 58,101 |
| b | 32 | 28 | 243 | 183 | 1,024 | 714 | 3,125 | 1,985 | 7,776 | 4,600 | 16,807 | 9,887 |
| b | 16 | 14 | 81 | 69 | 256 | 194 | 625 | 441 | 1,296 | 900 | 2,401 | 1,481 |
| b | 8 | 8 | 27 | 23 | 64 | 54 | 125 | ᘔ5 | 216 | 160 | 343 | 247 |
| b | 4 | 4 | 9 | 9 | 16 | 14 | 25 | 21 | 36 | 30 | 49 | 41 |
| b | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 7 |
| b | 0.5 | 0.6 | 0.3 | 0.4 | 0.25 | 0.3 | 0.2 | 0.2497 | 0.16 | 0.2 | 0.142857 | 0.186ᘔ35 |
| b | 0.25 | 0.3 | 0.1 | 0.14 | 0.0625 | 0.09 | 0.04 | 0.05915343ᘔ0 Ɛ62ᘔ68781Ɛ |
0.027 | 0.04 | 0.0204081632653 06122448979591 836734693877551 |
0.02Ɛ322547ᘔ05ᘔ 644ᘔ9380Ɛ908996 741Ɛ615771283Ɛ |
| Exponent | b=8 | b=9 | b=10 | b=11 | b=12 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | Dec. | Duod. | |
| b | 262,144 | 107,854 | 531,441 | 217,669 | 1,000,000 | 402,854 | 1,771,561 | 715,261 | 2,985,984 | 1,000,000 |
| b | 32,768 | 16,Ɛ68 | 59,049 | 2ᘔ,209 | 100,000 | 49,ᘔ54 | 161,051 | 79,24Ɛ | 248,832 | 100,000 |
| b | 4,096 | 2,454 | 6,561 | 3,969 | 10,000 | 5,954 | 14,641 | 8,581 | 20,736 | 10,000 |
| b | 512 | 368 | 729 | 509 | 1,000 | 6Ɛ4 | 1,331 | 92Ɛ | 1,728 | 1,000 |
| b | 64 | 54 | 81 | 69 | 100 | 84 | 121 | ᘔ1 | 144 | 100 |
| b | 8 | 8 | 9 | 9 | 10 | ᘔ | 11 | Ɛ | 12 | 10 |
| b | 0.125 | 0.16 | 0.1 | 0.14 | 0.1 | 0.12497 | 0.09 | 0.1 | 0.083 | 0.1 |
| b | 0.015625 | 0.023 | 0.012345679 | 0.0194 | 0.01 | 0.015343ᘔ0Ɛ6 2ᘔ68781Ɛ059 |
0.00826446280 99173553719 |
0.0123456789Ɛ | 0.00694 | 0.01 |
Some properties
(In this section, all numbers are written with duodecimal)
All squares end with square digits (i.e. end with 0, 1, 4 or 9), if n is divisible by both 2 and 3, then n ends with 0, if n is not divisible by 2 or 3, then n ends with 1, if n is divisible by 2 but not by 3, then n ends with 4, if n is not divisible by 2 but by 3, then n ends with 9. If the unit digit of n is 0, then the dozens digit of n is either 0 or 3, if the unit digit of n is 1, then the dozens digit of n is even, if the unit digit of n is 4, then the dozen digit of n is 0, 1, 4, 5, 8 or 9, if the unit digit of n is 9, then the dozen digit of n is either 0 or 6. (More specially, all squares of (primes ≥ 5) end with 1)
The digital root of a square is 1, 3, 4, 5 or Ɛ.
No repdigits with more than one digit are squares, in fact, a square cannot end with three same digits except 000.
No four-digit palindrome numbers are squares.
A cube can end with all digits except 2, 6 and ᘔ (in fact, no perfect powers end with 2, 6 or ᘔ), if n is not congruent to 2 mod 4, then n ends with the same digit as n; if n is congruent to 2 mod 4, then n ends with the digit (the last digit of n +- 6).
The digital root of a cube can be any number.
If k≥2, then n ends with the same digit as n.
Except for 6 and 24, all even perfect numbers end with 54.
The digital root of an even perfect number is 1, 4, 6 or ᘔ.
The unit digits of powers of 2 are 1, 2, 4, 8, 4, 8, 4, 8, 4, ... (periodic with period 2)
The unit digits of powers of 3 are 1, 3, 9, 3, 9, 3, 9, 3, 9, ... (periodic with period 2)
The unit digits of powers of 5 are 1, 5, 1, 5, 1, 5, 1, 5, 1, ... (periodic with period 2)
The unit digits of powers of 7 are 1, 7, 1, 7, 1, 7, 1, 7, 1, ... (periodic with period 2)
The unit digits of powers of Ɛ are 1, Ɛ, 1, Ɛ, 1, Ɛ, 1, Ɛ, 1, ... (periodic with period 2)
The final two digits of powers of 2 are 01, 02, 04, 08, 14, 28, 54, ᘔ8, 94, 68, 14, 28, 54, ᘔ8, 94, 68, 14, ... (periodic with period 6)
The final two digits of powers of 3 are 01, 03, 09, 23, 69, 83, 09, 23, 69, 83, 09, 23, 69, ... (periodic with period 4)
The final two digits of powers of 5 are 01, 05, 21, ᘔ5, 41, 85, 61, 65, 81, 45, ᘔ1, 25, 01, 05, 21, ᘔ5, 41, ... (periodic with period 10)
The final two digits of powers of 7 are 01, 07, 41, 47, 81, 87, 01, 07, 41, 47, 81, 87, 01, ... (periodic with period 6)
The final two digits of powers of Ɛ are 01, 0Ɛ, ᘔ1, 2Ɛ, 81, 4Ɛ, 61, 6Ɛ, 41, 8Ɛ, 21, ᘔƐ, 01, 0Ɛ, ᘔ1, 2Ɛ, 81, ... (periodic with period 10)
The digital roots of powers of 2 are 1, 2, 4, 8, 5, ᘔ, 9, 7, 3, 6, 1, 2, 4, 8, 5, ᘔ, 9, 7, 3, 6, 1, ... (periodic with period ᘔ)
The digital roots of powers of 3 are 1, 3, 9, 5, 4, 1, 3, 9, 5, 4, 1, ... (periodic with period 5)
The digital roots of powers of 5 are 1, 5, 3, 4, 9, 1, 5, 3, 4, 9, 1, ... (periodic with period 5)
The digital roots of powers of 7 are 1, 7, 5, 2, 3, ᘔ, 4, 6, 9, 8, 1, 7, 5, 2, 3, ᘔ, 4, 6, 9, 8, 1, ... (periodic with period ᘔ)
The digital roots of powers of Ɛ are 1, Ɛ, Ɛ, Ɛ, Ɛ, Ɛ, ... (periodic with period 1)
The period of the unit digit of powers of a number coprime to 10 is at most 2, the final two digit is at most 20, the final three digits is 200, the final four digits is 2000, ..., the final n digits is 2×10 (n≥2).
The unit digit of a Fibonacci number can be any digit except 6 (interestingly, if the unit digit of a Fibonacci number is 0, then the dozens digit of this number must also be 0, thus, all Fibonacci numbers divisible by 6 are also divisible by 100), and the unit digit of a Lucas number cannot be 0 or 9 (thus, no Lucas number is divisible by 10).
The unit digits of Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 1, 9, ᘔ, 7, 5, 0, 5, 5, ᘔ, 3, 1, 4, 5, 9, 2, Ɛ, 1, 0, 1, 1, 2, 3, 5, ... (periodic with period 20)
The unit digits of Lucas numbers are 2, 1, 3, 4, 7, Ɛ, 6, 5, Ɛ, 4, 3, 7, ᘔ, 5, 3, 8, Ɛ, 7, 6, 1, 7, 8, 3, Ɛ, 2, 1, 3, 4, 7, Ɛ, ... (periodic with period 20)
The final two digits of Fibonacci numbers are 00, 01, 01, 02, 03, 05, 08, 11, 19, 2ᘔ, 47, 75, 00, 75, 75, 2ᘔ, ᘔ3, 11, Ɛ4, 05, Ɛ9, 02, ƐƐ, 01, 00, 01, 01, 02, 03, 05, ... (periodic with period 20)
The final two digits of Lucas numbers are 02, 01, 03, 04, 07, 0Ɛ, 16, 25, 3Ɛ, 64, ᘔ3, 47, 2ᘔ, 75, ᘔ3, 58, 3Ɛ, 97, 16, Ɛ1, 07, Ɛ8, 03, ƐƐ, 02, 01, 03, 04, 07, 0Ɛ, ... (periodic with period 20)
The digital roots of Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 2, ᘔ, 1, Ɛ, 1, 1, 2, 3, 5, ... (periodic with period ᘔ)
The digital roots of Lucas numbers are 2, 1, 3, 4, 7, Ɛ, 7, 7, 3, ᘔ, 2, 1, 3, 4, 7, Ɛ, ... (periodic with period ᘔ)
The period of the unit digit of Fibonacci numbers is 20, the final two digits is also 20, the final three digits is 200, the final four digits is 2000, ..., the final n digits is 2×10 (n≥2).
All prime numbers end with prime digits or 1 (i.e. end with 1, 2, 3, 5, 7 or Ɛ), more generally, except for 2 and 3, all prime numbers end with 1, 5, 7 or Ɛ (1 and all prime digits that do not divide 10).
The density of primes end with 1 is a relatively low, but the density of primes end with 5, 7 and Ɛ are nearly equal. (since all prime squares except 4 and 9 end with 1, no prime squares end with 5, 7 or Ɛ)
Except (3, 5), all twin primes end with (5, 7) or (Ɛ, 1).
All palindrome primes except 11 has an odd number of digits, since all even-digit palindrome numbers are divisible by 11.
All lucky numbers end with digit 1, 3, 7 or 9.
Except for 3, all Fermat primes end with 5.
Except for 3, all Mersenne primes end with 7.
Except for 2 and 3, all Sophie Germain primes end with 5 or Ɛ.
Except for 5 and 7, all safe primes end with Ɛ.
A prime p is Gaussian prime if and only if p ends with 7 or Ɛ (or p=3).
A prime p is Eisenstein prime if and only if p ends with 5 or Ɛ (or p=2).
All full reptend primes end with 5 or 7. (in fact, for all primes p ≥ 5, (p-1)/(the period length of 1/p) is odd if and only if p is end with 5 or 7, since 10 is a quadratic nonresidue mod p if and only if p is end with 5 or 7)
If p is a safe prime other than 5, 7 and Ɛ, then the period length of 1/p is (p-1)/2. (this is not true for all primes ends with Ɛ (other than Ɛ itself), the first counterexample is p = 2ƐƐ, where the period length of 1/p is only 37)
By Fermat's little theorem, if p is a prime other than 2, 3 and Ɛ, then p divides the repunit with length p−1. (The converse is not true, the first counterexample is 55, which is composite (equals 5×11) but divides the repunit with length 54) Thus, we can prove that every positive integer coprime to 10 has a repunit multiple, and every positive integer has a multiple uses only 0's and 1's. (the smallest multiple of n uses only 0's and 1's are 1, 10, 10, 10, 101, 10, 1001, 100, 100, 1010, 11111111111, 10, 11, 10010, 1010, 100, ...)
The only two base 10 Wieferich primes < 10 are 1685 and 5Ɛ685, note that both of the numbers end with 685, and it is conjectured that all base 10 Wieferich primes end with 685.
Most numbers that end with 2 are nontotient (in fact, all nontotients < 58 except 2ᘔ end with 2), except 2 itself, the first counterexample is 92, which equals φ(ᘔ1) = φ(Ɛ).
All orders of non-cyclic simple group end with 0, however, we can prove that no groups with order 10, 20, 30 or 40 are simple, thus 50 is the smallest order of non-cyclic simple group, (50 is the order of the alternating group , which is a non-cyclic simple group) next three orders of non-cyclic simple group are 120, 260 and 360.
Some special numbers
(In this section, all numbers are written with duodecimal, using X for ten and E for eleven)
In duodecimal, as in decimal, there are special numbers that exhibit digit patterns when, for example, multiplied by small integers:
2497 * 1 = 2497 2497 * 2 = 4972 2497 * 3 = 7249 2497 * 4 = 9724 2497 * 5 = EEEE
186X35 * 1 = 186X35 186X35 * 2 = 35186X 186X35 * 3 = 5186X3 186X35 * 4 = 6X3518 186X35 * 5 = 86X351 186X35 * 6 = X35186 186X35 * 7 = EEEEEE
8579214E36429X7 * 1 = 8579214E36429X7 8579214E36429X7 * 2 = 14E36429X7085792 8579214E36429X7 * 3 = 214E36429X708579 8579214E36429X7 * 4 = 29X708579214E364 8579214E36429X7 * 5 = 36429X708579214E 8579214E36429X7 * 6 = 429X708579214E36 8579214E36429X7 * 7 = 4E36429X70857921 8579214E36429X7 * 8 = 579214E36429X708 8579214E36429X7 * 9 = 6429X708579214E3 8579214E36429X7 * X = 708579214E36429X 8579214E36429X7 * E = 79214E36429X7085 8579214E36429X7 * 10 = 8579214E36429X70 8579214E36429X7 * 11 = 9214E36429X70857 8579214E36429X7 * 12 = 9X708579214E3642 8579214E36429X7 * 13 = X708579214E36429 8579214E36429X7 * 14 = E36429X708579214 8579214E36429X7 * 15 = EEEEEEEEEEEEEEEE
123456789XE * 1 = 123456789XE 123456789XE * 2 = 2468E13579X 123456789XE * 3 = 36X147E2589 123456789XE * 4 = 4915X26E378 123456789XE * 5 = 5E4X3928167 123456789XE * 6 = 718293X4E56 123456789XE * 7 = 83E72X61945 123456789XE * 8 = 962E851X734 123456789XE * 9 = X8641E97523 123456789XE * X = EX987654312 123456789XE * E = 111111111101
123456789E * 1 = 123456789E (miss digit X) 123456789E * 2 = 2468E1357X (miss digit 9) 123456789E * 3 = 36X147E259 (miss digit 8) 123456789E * 4 = 4915X26E38 (miss digit 7) 123456789E * 5 = 5E4X392817 (miss digit 6) 123456789E * 6 = 718293X4E6 (miss digit 5) 123456789E * 7 = 83E72X6195 (miss digit 4) 123456789E * 8 = 962E851X74 (miss digit 3) 123456789E * 9 = X8641E9753 (miss digit 2) 123456789E * X = EX98765432 (miss digit 1) 123456789E * E = 11111111111
275 * 5 = 1111 275 * X = 2222 275 * 13 = 3333 275 * 18 = 4444 275 * 21 = 5555 275 * 26 = 6666 275 * 2E = 7777 275 * 34 = 8888 275 * 39 = 9999 275 * 42 = XXXX 275 * 47 = EEEE
1X537 * 7 = 111111 1X537 * 12 = 222222 1X537 * 19 = 333333 1X537 * 24 = 444444 1X537 * 2E = 555555 1X537 * 36 = 666666 1X537 * 41 = 777777 1X537 * 48 = 888888 1X537 * 53 = 999999 1X537 * 5X = XXXXXX 1X537 * 65 = EEEEEE
123456789E * E = 11111111111 123456789E * 1X = 22222222222 123456789E * 29 = 33333333333 123456789E * 38 = 44444444444 123456789E * 47 = 55555555555 123456789E * 56 = 66666666666 123456789E * 65 = 77777777777 123456789E * 74 = 88888888888 123456789E * 83 = 99999999999 123456789E * 92 = XXXXXXXXXXX 123456789E * X1 = EEEEEEEEEEE
92X79E43715865 * 15 = 1111111111111111 92X79E43715865 * 2X = 2222222222222222 92X79E43715865 * 43 = 3333333333333333 92X79E43715865 * 58 = 4444444444444444 92X79E43715865 * 71 = 5555555555555555 92X79E43715865 * 86 = 6666666666666666 92X79E43715865 * 9E = 7777777777777777 92X79E43715865 * E4 = 8888888888888888 92X79E43715865 * 109 = 9999999999999999 92X79E43715865 * 122 = XXXXXXXXXXXXXXXX 92X79E43715865 * 137 = EEEEEEEEEEEEEEEE
8327 * 17 = 111111 8327 * 32 = 222222 8327 * 49 = 333333 8327 * 64 = 444444 8327 * 7E = 555555 8327 * 96 = 666666 8327 * E1 = 777777 8327 * 108 = 888888 8327 * 123 = 999999 8327 * 13X = XXXXXX 8327 * 155 = EEEEEE
112233445566778899XE * EE = 1111111111111111111111 112233445566778899XE * 1EX = 2222222222222222222222 112233445566778899XE * 2E9 = 3333333333333333333333 112233445566778899XE * 3E8 = 4444444444444444444444 112233445566778899XE * 4E7 = 5555555555555555555555 112233445566778899XE * 5E6 = 6666666666666666666666 112233445566778899XE * 6E5 = 7777777777777777777777 112233445566778899XE * 7E4 = 8888888888888888888888 112233445566778899XE * 8E3 = 9999999999999999999999 112233445566778899XE * 9E2 = XXXXXXXXXXXXXXXXXXXXXX 112233445566778899XE * XE1 = EEEEEEEEEEEEEEEEEEEEEE
1^2 = 01, 0 + 1 = 1 E^2 = X1, X + 1 = E 56^2 = 2630, 26 + 30 = 56 66^2 = 3630, 36 + 30 = 66 EE^2 = EX01, EX + 01 = EE 444^2 = 170294, 170 + 294 = 444 778^2 = 4X4294, 4X4 + 294 = 778 EEE^2 = EEX001, EEX + 001 = EEE 12XX^2 = 1661144, 166 + 1144 = 12XX 1640^2 = 2401400, 240 + 1400 = 1640 2046^2 = 4161830, 416 + 1830 = 2046 2929^2 = 7802169, 780 + 2169 = 2929 3333^2 = X862469, X86 + 2469 = 3333 4973^2 = 1E062X69, 1E06 + 2X69 = 4973 5E60^2 = 2E603000, 2E60 + 3000 = 5E60
2^2 + 5^2 = 25 X^2 + 5^2 = X5 5^3 + 7^3 + 7^3 = 577 6^3 + 6^3 + 8^3 = 668 X^3 + 8^3 + 3^3 = X83 1^5 + 4^5 + 7^5 + 6^5 + 5^5 = 14765 9^5 + 3^5 + 8^5 + X^5 + 4^5 = 938X4 3^6 + 6^6 + 9^6 + 8^6 + 6^6 + 2^6 = 369862 X^6 + 2^6 + 3^6 + 9^6 + 4^6 + X^6 = X2394X
14 = (1 * 4)^2 20 = (2^2 + 0^2)! 21 = (2^2 + 1^2)^2 24 = 2^2 + 4! 30 = ((3 + 0)!)^2 43 = 4! + 3^3 48 = 4^3 - 8 84 = (8 + sqrt(4))^2 X1 = (X + 1)^2 X5 = (X - 5)^3 X8 = (X - 8)^7 XE = X + E^2 121 = (12 - 1)^2 169 = (1 * (6 + 9))^2 230 = (30 / 2)^2
1 * X + 1 = E
12 * X + 2 = EX
123 * X + 3 = EX9
1234 * X + 4 = EX98
12345 * X + 5 = EX987
123456 * X + 6 = EX9876
1234567 * X + 7 = EX98765
12345678 * X + 8 = EX987654
123456789 * X + 9 = EX9876543
123456789X * X + X = EX98765432
123456789XE * X + E = EX987654321
0 * E + 1 = 1
1 * E + 2 = 11
12 * E + 3 = 111
123 * E + 4 = 1111
1234 * E + 5 = 11111
12345 * E + 6 = 111111
123456 * E + 7 = 1111111
1234567 * E + 8 = 11111111
12345678 * E + 9 = 111111111
123456789 * E + X = 1111111111
123456789X * E + E = 11111111111
123456789XE * E + 10 = 111111111111
1^2 = 1
11^2 = 121
111^2 = 12321
1111^2 = 1234321
11111^2 = 123454321
111111^2 = 12345654321
1111111^2 = 1234567654321
11111111^2 = 123456787654321
111111111^2 = 12345678987654321
1111111111^2 = 123456789X987654321
11111111111^2 = 123456789XEX987654321
111111111111^2 = 123456789E00EX987654321 ((1_n)^2 is not palindrome number if n >= 10)
E^2 = X1
EE^2 = EX01
EEE^2 = EEX001
EEEE^2 = EEEX0001
EEEEE^2 = EEEEX00001
EEEEEE^2 = EEEEEX000001
EEEEEEE^2 = EEEEEEX0000001
EEEEEEEE^2 = EEEEEEEX00000001
EEEEEEEEE^2 = EEEEEEEEX000000001
EEEEEEEEEE^2 = EEEEEEEEEX0000000001
EEEEEEEEEEE^2 = EEEEEEEEEEX00000000001
EEEEEEEEEEEE^2 = EEEEEEEEEEEX000000000001
10XE * 1 = 10XE 10XE * 2 = 219X 10XE * 3 = 3289 10XE * 4 = 4378 10XE * 5 = 5467 10XE * 6 = 6556 10XE * 7 = 7645 10XE * 8 = 8734 10XE * 9 = 9823 10XE * X = X912 10XE * E = EX01
10EXE * 1 = 10EXE 10EXE * 2 = 21E9X 10EXE * 3 = 32E89 10EXE * 4 = 43E78 10EXE * 5 = 54E67 10EXE * 6 = 65E56 10EXE * 7 = 76E45 10EXE * 8 = 87E34 10EXE * 9 = 98E23 10EXE * X = X9E12 10EXE * E = EXE01
1 / E = 0.111111111111 ... 1 / 11 = 0.0E 0E 0E 0E 0E 0E ... 1 / EE = 0.01 01 01 01 01 01 ... 1 / 101 = 0.00EE 00EE 00EE ... 1 / E1 = 0.010EXE 010EXE ... 1 / 111 = 0.00E 00E 00E 00E ... 1 / X1 = 0.0123456789E 0123456789E ... 1 / 121 = 0.00X28466482X0 EE1937557391E ...
1 / XE1 = 0.00112233445566778899XE 00112233445566778899XE ... 1 / XEE1 = 0.000111222333444555666777888999XXE 000111222333444555666777888999XXE ... 1 / XEEE1 = 0.0000111122223333444455556666777788889999XXXE 0000111122223333444455556666777788889999XXXE ...
1 / EXEE = 0.00 01 01 02 03 05 08 11 19 2X 47 ... 1 / EEXEEE = 0.000 001 001 002 003 005 008 011 019 02X 047 075 100 175 275 42X 6X3 ... 1 / EEEXEEEE = 0.0000 0001 0001 0002 0003 0005 0008 0011 0019 002X 0047 0075 0100 0175 0275 042X 06X3 0E11 15E4 ...
1 / EXE01 = 0.0000101111212222323333434444545555656666767777878888989999X9XXXXEE 0000101111212222323333434444545555656666767777878888989999X9XXXXEE ...
1 / EX01 = 0.00 01 02 03 04 05 06 07 08 09 0X 0E 10 11 12 13 14 15 16 17 18 19 1X 1E 20 21 22 23 24 25 26 27 28 29 2X 2E 30 31 32 33 34 35 36 37 38 39 3X 3E 40 41 42 43 44 45 46 47 48 49 4X 4E 50 51 52 53 54 55 56 57 58 59 5X 5E 60 61 62 63 64 65 66 67 68 69 6X 6E 70 71 72 73 74 75 76 77 78 79 7X 7E 80 81 82 83 84 85 86 87 88 89 8X 8E 90 91 92 93 94 95 96 97 98 99 9X 9E X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 XX XE E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EE 00 01 02 03 04 05 06 07 08 09 0X 0E 10 11 12 13 14 15 16 17 18 19 1X 1E 20 21 22 23 24 25 26 27 28 29 2X 2E 30 31 32 33 34 35 36 37 38 39 3X 3E 40 41 42 43 44 45 46 47 48 49 4X 4E 50 51 52 53 54 55 56 57 58 59 5X 5E 60 61 62 63 64 65 66 67 68 69 6X 6E 70 71 72 73 74 75 76 77 78 79 7X 7E 80 81 82 83 84 85 86 87 88 89 8X 8E 90 91 92 93 94 95 96 97 98 99 9X 9E X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 XX XE E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EE ...
1 / EEX001 = 0.000 001 002 003 004 005 006 007 008 009 00X 00E 010 011 012 013 014 ... 1 / EEEX0001 = 0.0000 0001 0002 0003 0004 0005 0006 0007 0008 0009 000X 000E 0010 0011 0012 0013 0014 ...
1 / EX = 0.01 02 04 08 14 28 54 X8
194
368
714
1228
2454 ... (powers of 2)
1 / E9 = 0.01 03 09 23 69
183
509
1323
3969 ... (powers of 3)
1 / E8 = 0.01 04 14 54
194
714
2454 ... (powers of 4)
1 / XE = 0.0112358
11
19
2X
47
75
100
175
275
42X
6X3
E11
15E4 ... (Fibonacci numbers)
1 / 9E = 0.0125
10
25
5X
121
2X0
6X1
1462 ... (Pell numbers)
1 / 5E = 0.02 04 08 14 28 54 X8
194
368
714
1228
2454 ... (powers of 2)
1 / 3E = 0.03 09 23 69
183
509
1323
3969 ... (powers of 3)
1 / 2E = 0.04 14 54
194
714
2454 ... (powers of 4)
148421
28
54
X8
194
368
714
1228
1 / 1E = (powers of 2) ... 2454
23931
69
183
509
1323
1 / 2E = (power of 3) ... 3969
1441
54
194
714
1 / 3E = (power of 4) ... 2454
11853211
19
2X
47
75
100
175
275
42X
6X3
E11
1 / 10E = (Fibonacci numbers) ... 15E4
10521
25
5X
121
2X0
6X1
1 / 11E = (Pell numbers) ... 1462
ab * 5 * 25 = abab ab * 7 * 17 * 111 = ababab ab * 5 * 25 * 75 * 175 = abababab abc * 7 * 11 * 17 = abcabc abcd * 75 * 175 = abcdabcd
Prime numbers and divisibility rules
(In this section, all numbers are written with duodecimal)
A natural number (i.e. 1, 2, 3, 4, 5, 6, etc.) is called a prime number (or a prime) if it has exactly two positive divisors, 1 and the number itself. Natural numbers greater than 1 that are not prime are called composite.
The first 1ᘔ5 prime numbers (all the prime numbers less than 1000) are:
- 2, 3, 5, 7, Ɛ, 11, 15, 17, 1Ɛ, 25, 27, 31, 35, 37, 3Ɛ, 45, 4Ɛ, 51, 57, 5Ɛ, 61, 67, 6Ɛ, 75, 81, 85, 87, 8Ɛ, 91, 95, ᘔ7, ᘔƐ, Ɛ5, Ɛ7, 105, 107, 111, 117, 11Ɛ, 125, 12Ɛ, 131, 13Ɛ, 141, 145, 147, 157, 167, 16Ɛ, 171, 175, 17Ɛ, 181, 18Ɛ, 195, 19Ɛ, 1ᘔ5, 1ᘔ7, 1Ɛ1, 1Ɛ5, 1Ɛ7, 205, 217, 21Ɛ, 221, 225, 237, 241, 24Ɛ, 251, 255, 25Ɛ, 267, 271, 277, 27Ɛ, 285, 291, 295, 2ᘔ1, 2ᘔƐ, 2Ɛ1, 2ƐƐ, 301, 307, 30Ɛ, 315, 321, 325, 327, 32Ɛ, 33Ɛ, 347, 34Ɛ, 357, 35Ɛ, 365, 375, 377, 391, 397, 3ᘔ5, 3ᘔƐ, 3Ɛ5, 3Ɛ7, 401, 40Ɛ, 415, 41Ɛ, 421, 427, 431, 435, 437, 447, 455, 457, 45Ɛ, 465, 46Ɛ, 471, 481, 485, 48Ɛ, 497, 4ᘔ5, 4Ɛ1, 4ƐƐ, 507, 511, 517, 51Ɛ, 527, 531, 535, 541, 545, 557, 565, 575, 577, 585, 587, 58Ɛ, 591, 59Ɛ, 5Ɛ1, 5Ɛ5, 5Ɛ7, 5ƐƐ, 611, 615, 617, 61Ɛ, 637, 63Ɛ, 647, 655, 661, 665, 66Ɛ, 675, 687, 68Ɛ, 695, 69Ɛ, 6ᘔ7, 6Ɛ1, 701, 705, 70Ɛ, 711, 71Ɛ, 721, 727, 735, 737, 745, 747, 751, 767, 76Ɛ, 771, 775, 77Ɛ, 785, 791, 797, 7ᘔ1, 7ƐƐ, 801, 80Ɛ, 817, 825, 82Ɛ, 835, 841, 851, 855, 85Ɛ, 865, 867, 871, 881, 88Ɛ, 8ᘔ5, 8ᘔ7, 8ᘔƐ, 8Ɛ5, 8Ɛ7, 901, 905, 907, 90Ɛ, 91Ɛ, 921, 927, 955, 95Ɛ, 965, 971, 987, 995, 9ᘔ7, 9ᘔƐ, 9Ɛ1, 9Ɛ5, 9ƐƐ, ᘔ07, ᘔ0Ɛ, ᘔ11, ᘔ17, ᘔ27, ᘔ35, ᘔ37, ᘔ3Ɛ, ᘔ41, ᘔ45, ᘔ4Ɛ, ᘔ5Ɛ, ᘔ6Ɛ, ᘔ77, ᘔ87, ᘔ91, ᘔ95, ᘔ9Ɛ, ᘔᘔ7, ᘔᘔƐ, ᘔƐ7, ᘔƐƐ, Ɛ11, Ɛ15, Ɛ1Ɛ, Ɛ21, Ɛ25, Ɛ2Ɛ, Ɛ31, Ɛ37, Ɛ45, Ɛ61, Ɛ67, Ɛ6Ɛ, Ɛ71, Ɛ91, Ɛ95, Ɛ97, Ɛᘔ5, ƐƐ5, ƐƐ7
Except 2 and 3, all primes end in 1, 5, 7 or Ɛ. The first k such that all of 10k, 10k + 1, 10k + 2, ..., 10k + Ɛ are all composite is 38, i.e. all of 380, 381, 382, ..., 38Ɛ are composite.
The density of primes end with 1 is a relatively low, but the density of primes end with 5, 7 and Ɛ are nearly equal. (i.e. for a given natural number N, the numbers of primes end with 1 less than N is usually smaller than the number of primes end with 5 (or 7, or Ɛ) less than N)
There are 2ᘔ primes between 1 and 100, 23 primes between 101 and 200, 1ᘔ primes between 201 and 300, 1ᘔ primes between 301 and 400, 1Ɛ primes between 401 and 500, 1ᘔ primes between 501 and 600, 16 primes between 601 and 700, 1ᘔ primes between 701 and 800, 18 primes between 801 and 900, 16 primes between 901 and ᘔ00, 1ᘔ primes between ᘔ01 and Ɛ00, 17 primes between Ɛ01 and 1000.
- This section focuses on duodecimal divisibility rules.
- 1
Any integer is divisible by 1.
- 2
If a number is divisible by 2 then the unit digit of that number will be 0, 2, 4, 6, 8 or ᘔ.
- 3
If a number is divisible by 3 then the unit digit of that number will be 0, 3, 6 or 9.
- 4
If a number is divisible by 4 then the unit digit of that number will be 0, 4 or 8.
- 5
To test for divisibility by 5, double the units digit and subtract the result from the number formed by the rest of the digits. If the result is divisible by 5 then the given number is divisible by 5.
This rule comes from 21(5*5)
Examples:
13 rule => |1-2*3| = 5 which is divisible by 5.
2Ɛᘔ5 rule => |2Ɛᘔ-2*5| = 2Ɛ0(5*70) which is divisible by 5(or apply the rule on 2Ɛ0).
OR
To test for divisibility by 5, subtract the units digit and triple of the result to the number formed by the rest of the digits. If the result is divisible by 5 then the given number is divisible by 5.
This rule comes from 13(5*3)
Examples:
13 rule => |3-3*1| = 0 which is divisible by 5.
2Ɛᘔ5 rule => |5-3*2Ɛᘔ| = 8Ɛ1(5*195) which is divisible by 5(or apply the rule on 8Ɛ1).
OR
Form the alternating sum of blocks of two from right to left. If the result is divisible by 5 then the given number is divisible by 5.
This rule comes from 101, since 101 = 5*25, thus this rule can be also tested for the divisibility by 25.
Example:
97,374,627 => 27-46+37-97 = -7Ɛ which is divisible by 5.
- 6
If a number is divisible by 6 then the unit digit of that number will be 0 or 6.
- 7
To test for divisibility by 7, triple the units digit and add the result to the number formed by the rest of the digits. If the result is divisible by 7 then the given number is divisible by 7.
This rule comes from 2Ɛ(7*5)
Examples:
12 rule => |3*2+1| = 7 which is divisible by 7.
271Ɛ rule => |3*Ɛ+271| = 29ᘔ(7*4ᘔ) which is divisible by 7(or apply the rule on 29ᘔ).
OR
To test for divisibility by 7, subtract the units digit and double the result from the number formed by the rest of the digits. If the result is divisible by 7 then the given number is divisible by 7.
This rule comes from 12(7*2)
Examples:
12 rule => |2-2*1| = 0 which is divisible by 7.
271Ɛ rule => |Ɛ-2*271| = 513(7*89) which is divisible by 7(or apply the rule on 513).
OR
To test for divisibility by 7, 4 times the units digit and subtract the result from the number formed by the rest of the digits. If the result is divisible by 7 then the given number is divisible by 7.
This rule comes from 41(7*7)
Examples:
12 rule => |4*2-1| = 7 which is divisible by 7.
271Ɛ rule => |4*Ɛ-271| = 235(7*3Ɛ) which is divisible by 7(or apply the rule on 235).
OR
Form the alternating sum of blocks of three from right to left. If the result is divisible by 7 then the given number is divisible by 7.
This rule comes from 1001, since 1001 = 7*11*17, thus this rule can be also tested for the divisibility by 11 and 17.
Example:
386,967,443 => 443-967+386 = -168 which is divisible by 7.
- 8
If the 2-digit number formed by the last 2 digits of the given number is divisible by 8 then the given number is divisible by 8.
Example: 1Ɛ48, 4120
rule => since 48(8*7) divisible by 8, then 1Ɛ48 is divisible by 8.
rule => since 20(8*3) divisible by 8, then 4120 is divisible by 8.
- 9
If the 2-digit number formed by the last 2 digits of the given number is divisible by 9 then the given number is divisible by 9.
Example: 7423, 8330
rule => since 23(9*3) divisible by 9, then 7423 is divisible by 9.
rule => since 30(9*4) divisible by 9, then 8330 is divisible by 9.
- ᘔ
If the number is divisible by 2 and 5 then the number is divisible by ᘔ.
- Ɛ
If the sum of the digits of a number is divisible by Ɛ then the number is divisible by Ɛ (the equivalent of casting out nines in decimal).
Example: 29, 61Ɛ13
rule => 2+9 = Ɛ which is divisible by Ɛ, then 29 is divisible by Ɛ.
rule => 6+1+Ɛ+1+3 = 1ᘔ which is divisible by Ɛ, then 61Ɛ13 is divisible by Ɛ.
- 10
If a number is divisible by 10 then the unit digit of that number will be 0.
- 11
Sum the alternate digits and subtract the sums. If the result is divisible by 11 the number is divisible by 11 (the equivalent of divisibility by eleven in decimal).
Example: 66, 9427
rule => |6-6| = 0 which is divisible by 11, then 66 is divisible by 11.
rule => |(9+2)-(4+7)| = |ᘔ-ᘔ| = 0 which is divisible by 11, then 9427 is divisible by 11.
- 12
If the number is divisible by 2 and 7 then the number is divisible by 12.
- 13
If the number is divisible by 3 and 5 then the number is divisible by 13.
- 14
If the 2-digit number formed by the last 2 digits of the given number is divisible by 14 then the given number is divisible by 14.
Fractions and irrational numbers
Fractions
Duodecimal fractions may be simple:
- 1/2 = 0.6
- 1/3 = 0.4
- 1/4 = 0.3
- 1/6 = 0.2
- 1/8 = 0.16
- 1/9 = 0.14
- 1/10 = 0.1 (note that this is a twelfth, 1/ᘔ is a tenth)
- 1/14 = 0.09 (note that this is a sixteenth, 1/12 is a fourteenth)
or complicated:
- 1/5 = 0.249724972497... recurring (rounded to 0.24ᘔ)
- 1/7 = 0.186ᘔ35186ᘔ35... recurring (rounded to 0.187)
- 1/ᘔ = 0.1249724972497... recurring (rounded to 0.125)
- 1/Ɛ = 0.111111111111... recurring (rounded to 0.111)
- 1/11 = 0.0Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0Ɛ... recurring (rounded to 0.0Ɛ1)
- 1/12 = 0.0ᘔ35186ᘔ35186... recurring (rounded to 0.0ᘔ3)
- 1/13 = 0.0972497249724... recurring (rounded to 0.097)
| Examples in duodecimal | Decimal equivalent |
|---|---|
| 1 × (5/8) = 0.76 | 1 × (5/8) = 0.625 |
| 100 × (5/8) = 76 | 144 × (5/8) = 90 |
| 576/9 = 76 | 810/9 = 90 |
| 400/9 = 54 | 576/9 = 64 |
| 1ᘔ.6 + 7.6 = 26 | 22.5 + 7.5 = 30 |
As explained in recurring decimals, whenever an irreducible fraction is written in radix point notation in any base, the fraction can be expressed exactly (terminates) if and only if all the prime factors of its denominator are also prime factors of the base. Thus, in base-ten (= 2×5) system, fractions whose denominators are made up solely of multiples of 2 and 5 terminate: 1/8 = 1/(2×2×2), 1/20 = 1/(2×2×5) and 1/500 = 1/(2×2×5×5×5) can be expressed exactly as 0.125, 0.05 and 0.002 respectively. 1/3 and 1/7, however, recur (0.333... and 0.142857142857...). In the duodecimal (= 2×2×3) system, 1/8 is exact; 1/20 and 1/500 recur because they include 5 as a factor; 1/3 is exact; and 1/7 recurs, just as it does in decimal.
The number of denominators which give terminating fractions within a given number of digits, say n, in a base b is the number of factors (divisors) of b, the nth power of the base b (although this includes the divisor 1, which does not produce fractions when used as the denominator). The number of factors of b is given using its prime factorization.
For decimal, 10 = 2 * 5. The number of divisors is found by adding one to each exponent of each prime and multiplying the resulting quantities together. Factors of 10 = (n+1)(n+1) = (n+1).
For example, the number 8 is a factor of 10 (1000), so 1/8 and other fractions with a denominator of 8 can not require more than 3 fractional decimal digits to terminate. 5/8 = 0.625ten
For duodecimal, 12 = 2 * 3. This has (2n+1)(n+1) divisors. The sample denominator of 8 is a factor of a gross (12 = 144), so eighths can not need more than two duodecimal fractional places to terminate. 5/8 = 0.76twelve
Because both ten and twelve have two unique prime factors, the number of divisors of b for b = 10 or 12 grows quadratically with the exponent n (in other words, of the order of n).
Recurring digits
The Dozenal Society of America argues that factors of 3 are more commonly encountered in real-life division problems than factors of 5. Thus, in practical applications, the nuisance of repeating decimals is encountered less often when duodecimal notation is used. Advocates of duodecimal systems argue that this is particularly true of financial calculations, in which the twelve months of the year often enter into calculations.
However, when recurring fractions do occur in duodecimal notation, they are less likely to have a very short period than in decimal notation, because 12 (twelve) is between two prime numbers, 11 (eleven) and 13 (thirteen), whereas ten is adjacent to the composite number 9. Nonetheless, having a shorter or longer period doesn't help the main inconvenience that one does not get a finite representation for such fractions in the given base (so rounding, which introduces inexactitude, is necessary to handle them in calculations), and overall one is more likely to have to deal with infinite recurring digits when fractions are expressed in decimal than in duodecimal, because one out of every three consecutive numbers contains the prime factor 3 in its factorization, whereas only one out of every five contains the prime factor 5. All other prime factors, except 2, are not shared by either ten or twelve, so they do not influence the relative likeliness of encountering recurring digits (any irreducible fraction that contains any of these other factors in its denominator will recur in either base). Also, the prime factor 2 appears twice in the factorization of twelve, whereas only once in the factorization of ten; which means that most fractions whose denominators are powers of two will have a shorter, more convenient terminating representation in duodecimal than in decimal representation (e.g. 1/(2) = 0.25 ten = 0.3 twelve; 1/(2) = 0.125 ten = 0.16 twelve; 1/(2) = 0.0625 ten = 0.09 twelve; 1/(2) = 0.03125 ten = 0.046 twelve; etc.).
Values in bold indicate that value is exact.
| Decimal base Prime factors of the base: 2, 5 Prime factors of one below the base: 3 Prime factors of one above the base: 11 All other primes: 7 13 17 19 23 29 31 |
Duodecimal base Prime factors of the base: 2, 3 Prime factors of one below the base: Ɛ Prime factors of one above the base: 11 All other primes: 5 7 15 17 1Ɛ 25 27 | ||||
| Fraction | Prime factors of the denominator |
Positional representation | Positional representation | Prime factors of the denominator |
Fraction |
|---|---|---|---|---|---|
| 1/2 | 2 | 0.5 | 0.6 | 2 | 1/2 |
| 1/3 | 3 | 0.3 | 0.4 | 3 | 1/3 |
| 1/4 | 2 | 0.25 | 0.3 | 2 | 1/4 |
| 1/5 | 5 | 0.2 | 0.2497 | 5 | 1/5 |
| 1/6 | 2, 3 | 0.16 | 0.2 | 2, 3 | 1/6 |
| 1/7 | 7 | 0.142857 | 0.186ᘔ35 | 7 | 1/7 |
| 1/8 | 2 | 0.125 | 0.16 | 2 | 1/8 |
| 1/9 | 3 | 0.1 | 0.14 | 3 | 1/9 |
| 1/10 | 2, 5 | 0.1 | 0.12497 | 2, 5 | 1/ᘔ |
| 1/11 | 11 | 0.09 | 0.1 | Ɛ | 1/Ɛ |
| 1/12 | 2, 3 | 0.083 | 0.1 | 2, 3 | 1/10 |
| 1/13 | 13 | 0.076923 | 0.0Ɛ | 11 | 1/11 |
| 1/14 | 2, 7 | 0.0714285 | 0.0ᘔ35186 | 2, 7 | 1/12 |
| 1/15 | 3, 5 | 0.06 | 0.09724 | 3, 5 | 1/13 |
| 1/16 | 2 | 0.0625 | 0.09 | 2 | 1/14 |
| 1/17 | 17 | 0.0588235294117647 | 0.08579214Ɛ36429ᘔ7 | 15 | 1/15 |
| 1/18 | 2, 3 | 0.05 | 0.08 | 2, 3 | 1/16 |
| 1/19 | 19 | 0.052631578947368421 | 0.076Ɛ45 | 17 | 1/17 |
| 1/20 | 2, 5 | 0.05 | 0.07249 | 2, 5 | 1/18 |
| 1/21 | 3, 7 | 0.047619 | 0.06ᘔ3518 | 3, 7 | 1/19 |
| 1/22 | 2, 11 | 0.045 | 0.06 | 2, Ɛ | 1/1ᘔ |
| 1/23 | 23 | 0.0434782608695652173913 | 0.06316948421 | 1Ɛ | 1/1Ɛ |
| 1/24 | 2, 3 | 0.0416 | 0.06 | 2, 3 | 1/20 |
| 1/25 | 5 | 0.04 | 0.05915343ᘔ0Ɛ62ᘔ68781Ɛ | 5 | 1/21 |
| 1/26 | 2, 13 | 0.0384615 | 0.056 | 2, 11 | 1/22 |
| 1/27 | 3 | 0.037 | 0.054 | 3 | 1/23 |
| 1/28 | 2, 7 | 0.03571428 | 0.05186ᘔ3 | 2, 7 | 1/24 |
| 1/29 | 29 | 0.0344827586206896551724137931 | 0.04Ɛ7 | 25 | 1/25 |
| 1/30 | 2, 3, 5 | 0.03 | 0.04972 | 2, 3, 5 | 1/26 |
| 1/31 | 31 | 0.032258064516129 | 0.0478ᘔᘔ093598166Ɛ74311Ɛ28623ᘔ55 | 27 | 1/27 |
| 1/32 | 2 | 0.03125 | 0.046 | 2 | 1/28 |
| 1/33 | 3, 11 | 0.03 | 0.04 | 3, Ɛ | 1/29 |
| 1/34 | 2, 17 | 0.02941176470588235 | 0.0429ᘔ708579214Ɛ36 | 2, 15 | 1/2ᘔ |
| 1/35 | 5, 7 | 0.0285714 | 0.0414559Ɛ3931 | 5, 7 | 1/2Ɛ |
| 1/36 | 2, 3 | 0.027 | 0.04 | 2, 3 | 1/30 |
The duodecimal period length of 1/n are
- 0, 0, 0, 0, 4, 0, 6, 0, 0, 4, 1, 0, 2, 6, 4, 0, 16, 0, 6, 4, 6, 1, 11, 0, 20, 2, 0, 6, 4, 4, 30, 0, 1, 16, 12, 0, 9, 6, 2, 4, 40, 6, 42, 1, 4, 11, 23, 0, 42, 20, 16, 2, 52, 0, 4, 6, 6, 4, 29, 4, 15, 30, 6, 0, 4, 1, 66, 16, 11, 12, 35, 0, ... (sequence A246004 in the OEIS)
The duodecimal period length of 1/(nth prime) are
- 0, 0, 4, 6, 1, 2, 16, 6, 11, 4, 30, 9, 40, 42, 23, 52, 29, 15, 66, 35, 36, 26, 41, 8, 16, 100, 102, 53, 54, 112, 126, 65, 136, 138, 148, 150, 3, 162, 83, 172, 89, 90, 95, 24, 196, 66, 14, 222, 113, 114, 8, 119, 120, 125, 256, 131, 268, 54, 138, 280, ... (sequence A246489 in the OEIS)
Smallest prime with duodecimal period n are
- 11, 13, 157, 5, 22621, 7, 659, 89, 37, 19141, 23, 20593, 477517, 211, 61, 17, 2693651, 1657, 29043636306420266077, 85403261, 8177824843189, 57154490053, 47, 193, 303551, 79, 306829, 673, 59, 31, 373, 153953, 886381, 2551, 71, 73, ... (sequence A252170 in the OEIS)
Irrational numbers
As for irrational numbers, none of them have a finite representation in any of the rational-based positional number systems (such as the decimal and duodecimal ones); this is because a rational-based positional number system is essentially nothing but a way of expressing quantities as a sum of fractions whose denominators are powers of the base, and by definition no finite sum of rational numbers can ever result in an irrational number. For example, 123.456 = 1 × 10 + 2 × 10 + 3 × 10 + 4 × 1/10 + 5 × 1/10 + 6 × 1/10 (this is also the reason why fractions that contain prime factors in their denominator not in common with those of the base do not have a terminating representation in that base). Moreover, the infinite series of digits of an irrational number does not exhibit a strictly repeating pattern; instead, the different digits often succeed in a seemingly random fashion. The following chart compares the first few digits of the decimal and duodecimal representation of several of the most important algebraic and transcendental irrational numbers. Some of these numbers may be perceived as having fortuitous patterns, making them easier to memorize, when represented in one base or the other.
| Algebraic irrational number | In decimal | In duodecimal |
|---|---|---|
| √2 (the length of the diagonal of a unit square) | 1.41421356237309... (≈ 1.4142) | 1.4Ɛ79170ᘔ07Ɛ857... (≈ 1.5) |
| √3 (the length of the diagonal of a unit cube, or twice the height of an equilateral triangle of unit side) | 1.73205080756887... (≈ 1.732) | 1.894Ɛ97ƐƐ968704... (≈ 1.895) |
| √5 (the length of the diagonal of a 1×2 rectangle) | 2.2360679774997... (≈ 2.236) | 2.29ƐƐ132540589... (≈ 2.2ᘔ) |
| φ (phi, the golden ratio = ) | 1.6180339887498... (≈ 1.618) | 1.74ƐƐ6772802ᘔ4... (≈ 1.75) |
| Transcendental irrational number | In decimal | In duodecimal |
| π (pi, the ratio of circumference to diameter) | 3.1415926535897932384626433 8327950288419716939937510... (≈ 3.1416) |
3.184809493Ɛ918664573ᘔ6211Ɛ Ɛ151551ᘔ05729290ᘔ7809ᘔ492... (≈ 3.1848) |
| e (the base of the natural logarithm) | 2.718281828459045... (≈ 2.718) | 2.8752360698219Ɛ8... (≈ 2.875) |
The first few digits of the decimal and duodecimal representation of another important number, the Euler–Mascheroni constant (the status of which as a rational or irrational number is not yet known), are:
| Number | In decimal | In duodecimal |
|---|---|---|
| γ (the limiting difference between the harmonic series and the natural logarithm) | 0.57721566490153... (≈ 0.577) | 0.6Ɛ15188ᘔ6760Ɛ3... (≈ 0.7) |
See also
- Senary (base 6)
- Decimal (base 10)
- Sexagesimal (base 60)
References
- Pitman, Isaac (ed.): A triple (twelve gross) Gems of Wisdom. London 1860
- ^ "Unicode 8.0.0". Unicode Consortium. Retrieved 2016-05-30.
- "The Unicode Standard 8.0" (PDF). Retrieved 2014-07-18.
- George Dvorsky (2013-01-18). "Why We Should Switch To A Base-12 Counting System". Archived from the original on 2013-01-21. Retrieved 2013-12-21.
{{cite web}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help) - Matsushita, Shuji (1998). Decimal vs. Duodecimal: An interaction between two systems of numeration. 2nd Meeting of the AFLANG, October 1998, Tokyo. Archived from the original on 2008-10-05. Retrieved 2011-05-29Template:Inconsistent citations
{{cite conference}}: CS1 maint: postscript (link) - Mazaudon, Martine (2002). "Les principes de construction du nombre dans les langues tibéto-birmanes". In François, Jacques (ed.). La Pluralité (PDF). Leuven: Peeters. pp. 91–119. ISBN 90-429-1295-2Template:Inconsistent citations
{{cite book}}: CS1 maint: postscript (link) - von Mengden, Ferdinand (2006). "The peculiarities of the Old English numeral system". Medieval English and its Heritage: Structure Meaning and Mechanisms of Change. Studies in English Medieval Language and Literature. Vol. 16. Frankfurt: Peter Lang Pub. pp. 125–45.
{{cite book}}: Unknown parameter|editors=ignored (|editor=suggested) (help)
von Mengden, Ferdinand (2010). Cardinal Numerals: Old English from a Cross-Linguistic Perspective. Topics in English Linguistics. Vol. 67. Berlin; New York: De Gruyter Mouton. pp. 159–161. - Pittman, Richard. 1990. Origin of Mesopotamian duodecimal and sexagesimal counting systems. Philippine Journal of Linguistics 21(1)"97.
- Nishikawa, Yoshiaki (2002). "ヒマラヤの満月と十二進法 (The Full Moon in the Himalayas and the Duodecimal System)". Archived from the original on March 29, 2008. Retrieved 2008-03-24Template:Inconsistent citations
{{cite web}}: Unknown parameter|deadurl=ignored (|url-status=suggested) (help)CS1 maint: postscript (link) - Ifrah, Georges (2000). The Universal History of Numbers: From prehistory to the invention of the computer. John Wiley and Sons. ISBN 0-471-39340-1Template:Inconsistent citations
{{cite book}}: CS1 maint: postscript (link). Translated from the French by David Bellos, E.F. Harding, Sophie Wood and Ian Monk. - Macey, Samuel L. (1989). The Dynamics of Progress: Time, Method, and Measure. Atlanta, Georgia: University of Georgia Press. p. 92. ISBN 978-0-8203-3796-8Template:Inconsistent citations
{{cite book}}: CS1 maint: postscript (link) - ^ De Vlieger, Michael (2010). "Symbology Overview" (PDF). The Duodecimal Bulletin. 4X (2).
- Andrews, Frank Emerson (1935). New Numbers: How Acceptance of a Duodecimal (12) Base Would Simplify Mathematics. p. 52.
- Pitman, Isaac (1947). "A Reckoning Reform [reprint from 1857]" (PDF). The Duodecimal Bulletin. 3 (2).
- ^ "Mo for Megro" (PDF). The Duodecimal Bulletin. 1 (1). 1945.
- ^ "The Unicode Standard, Version 8.0: Number Forms" (PDF). Unicode Consortium. Retrieved 2016-05-30.
- "What should the DSA do about transdecimal characters? | The Dozenal Society of America". www.dozenal.org. Retrieved 2018-01-01.
- ^ Volan, John (July 2015). "Base Annotation Schemes" (PDF). Duodecomal Bulletin. 62.
- "Annual Meeting of 1973 and Meeting of the Board" (PDF). The Duodecimal Bulletin. 25 (1). 1974.
- De Vlieger, Michael (2008). "Going Classic" (PDF). The Duodecimal Bulletin. 49 (2).
- ^ Zirkel, Gene (2010). "How Do You Pronounce Dozenals?" (PDF). The Duodecimal Bulletin. 4E (2).
- Carroll, Lee (1995). Kryon—Alchemy of the Human Spirit. The Kryon Writings, Inc. ISBN 0-9636304-8-2.
- "Little Twelvetoes"
- Karl Pentzlin (2013-03-30). "Proposal to encode Duodecimal Digit Forms in the UCS" (PDF). ISO/IEC JTC1/SC2/WG2, Document N4399. Retrieved 2016-05-30.
- "U+218C". www.fileformat.info. Retrieved 2018-01-02.
- Scott Pakin (2009). "The Comprehensive LATEX Symbol List" (PDF). Retrieved 2016-05-30.
- Pendlebury, Tom (May 2011). "TGM. A coherent dozenal metrology based on Time, Gravity and Mass" (PDF). The Dozenal Society of Great Britain.
- Suga, Takashi (2002). "Proposal for the Universal Unit System".
- http://www.dozenal.org/articles/DSA-DozenalFAQs.pdf
External links
- Dozenal Society of America
- Dozenal Society of Great Britain website
- Duodecimal calculator
- Comprehensive Synopsis of Dozenal and Transdecimal Symbologies
- Base Annotation Schemes
- Duodecimal Avtukh
- Grime, James. "Base 12: Dozenal or Duodecimal". Numberphile. Brady Haran.
 , which is a non-cyclic simple group) next three orders of non-cyclic simple group are 120, 260 and 360.
, which is a non-cyclic simple group) next three orders of non-cyclic simple group are 120, 260 and 360.
 )
)