This is an old revision of this page, as edited by Trainspotter~enwiki (talk | contribs) at 16:25, 10 June 2003 (Add image to proof). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 16:25, 10 June 2003 by Trainspotter~enwiki (talk | contribs) (Add image to proof)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)
The Pythagorean theorem or Pythagoras' theorem is named after and commonly attributed to the 6th century BC Greek philosopher and mathematician Pythagoras, though the facts of the theorem were known before he lived. The theorem states:
- The sum of the areas of the squares on the legs of a right triangle is equal to the area of the square on the hypotenuse.
(A right triangle is one with a right angle; the legs are the two sides that make up the right angle; the hypotenuse is the third side opposite the right angle; the square on a side of the triangle is a square, one of whose sides is that side of the triangle).
Image of a right triangle to illustrate the Pythagorean Theorem
Since the area of a square is the square of the length of a side, we can also formulate the theorem as:
- Given a right triangle, with legs of lengths a and b and hypotenuse of length c, then
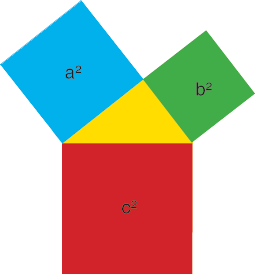 |
Proof: (see image, right) Draw a right triangle with sides a, b, and c as above. Then take a copy of this triangle and place its a side in line with the b side of the first, so that their c sides form a right angle (this is possible because the angles in any triangle add up to two right angles -- think it through). Then place the a side of a third triangle in line with the b side of the second, again in such a manner that the c sides form a right angle. Finally, complete a square of side (a+b) by placing the a side of a fourth triangle in line with the b side of the third. On the one hand, the area of this square is (a+b) because (a+b) is the length of its sides. On the other hand, the square is made up of four equal triangles each having area ab/2 plus one square in the middle of side length c. So the total area of the square can also be written as 4 · ab/2 + c. We may set those two expressions equal to each other and simplify:
Note that this proof does not work in non-euclidean geometries, since, say, on a sphere, the angles of a triangle don't add up to 180 degrees, and the above "square" cannot be formed.
The sheer volume of distinct known proofs of this theorem is staggering. See the external links below for just a sampling.
The converse of the Pythagorean Theorem is also true: if you have three positive numbers a, b, and c such that a+b=c, then there exists a triangle with sides a, b and c, and every such triangle has a right angle between the sides a and b. This can be proven using the law of cosines which is a generalization of the Pythagorean theorem applying to all triangles, not just right-angled ones.
Another generalization of the Pythagorean Theorem was already given by Euclid in his Elements: if one erects similar figures (see Geometry) on the sides of a right triangle, then the sum of the areas of the two smaller ones equals the area of the larger one.
Yet another generalization of the Pythagorean Theorem is Parseval's identity in inner product spaces.
The Pythagorean Theorem also generalizes to higher-dimensional simplexes. If a tetrahedron has a right angle corner (a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This is called de Gua's theorem.
One should note that the Pythagorean Theorem is derived from the axioms of Euclidean geometry and does not apply to triangles in non-Euclidean spaces such as the surface of a sphere. A priori, it need not be true for actually existing triangles that we measure out in our Universe, since the Universe could be non-Euclidean. One of the first mathematicians to realize this was Carl Friedrich Gauss, who then carefully measured out large right triangles as part of his geographical surveys in order to check the theorem. He found no counterexamples to the theorem within his measurement precision. The theory of general relativity holds that matter and energy cause space to be non-Euclidean and the theorem does therefore not strictly apply in the presense of matter or energy. However, the deviation from Euclidean space is small except near strong gravitational sources such as black holes. Whether the theorem is violated over large cosmological scales is an open problem of cosmology.
The Pythagorean Theorem also has applications in physics, mathematics, and computer science. Given two vectors, A and B, the Pythagorean Theorem states if ||A + B|| = ||A|| + ||B||, then the two vectors are orthogonal.
See also:


