This is an old revision of this page, as edited by WikiCleanerBot (talk | contribs) at 06:12, 19 December 2024 (v2.05b - Bot T20 CW#61 - Fix errors for CW project (Reference before punctuation)). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 06:12, 19 December 2024 by WikiCleanerBot (talk | contribs) (v2.05b - Bot T20 CW#61 - Fix errors for CW project (Reference before punctuation))(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)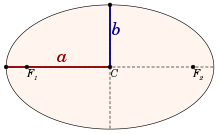
| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Perimeter of an ellipse" – news · newspapers · books · scholar · JSTOR (December 2024) (Learn how and when to remove this message) |
Unlike most other elementary shapes, such as the circle and square, there is no algebraic equation to determine the perimeter of an ellipse. Throughout history, a large number of equations for approximations and estimates have been made for the perimeter of an ellipse.
Mathematical background
An ellipse is defined by two axes: the major axis (the longest diameter, ) and the minor axis (the shortest diameter, ). The exact perimeter of an ellipse is given by the integral:
where is the eccentricity of the ellipse, defined as
The integral used to find the area does not have a closed-form solution in terms of elementary functions. Another solution for the perimeter, this time using infinite sums, is:
Approximations
Because the exact computation involves elliptic integrals, several approximations have been developed over time.
Ramanujan's approximations
Indian mathematician Srinivasa Ramanujan proposed multiple approximations:
First Approximation:
Second Approximation:
where
Simple arithmetic-geometric mean approximation
This formula is simpler than most perimeter formulas but less accurate for highly eccentric ellipses.
Approximations made from programs
In more recent years, computer programs have been used to find and calculate more precise approximations of the perimeter of an ellipse. In an online video about the perimeter of an ellipse, recreational mathematician and YouTuber Matt Parker, using a computer program, calculated numerous approximations for the perimeter of an ellipse. Approximations Parker found include:
References
- Chandrupatla & Osler, Tirupathi & Thomas (2010). "The Perimeter of an Ellipse" (PDF). Math Scientist.
- Abbott, Paul. "On the Perimeter of an Ellipse" (PDF). The Mathematical Journal: 2.
- Villarino, Mark B. (February 1, 2008). "Ramanujan's Perimeter of an Ellipse". Escuela de Matemática, Universidad de Costa Rica.
- Stand-up Maths (2020-09-05). Why is there no equation for the perimeter of an ellipse‽. Retrieved 2024-12-16 – via YouTube.
 ) and the minor axis (the shortest diameter,
) and the minor axis (the shortest diameter,  ). The exact perimeter
). The exact perimeter  of an ellipse is given by the integral:
of an ellipse is given by the integral:

 is the eccentricity of the ellipse, defined as
is the eccentricity of the ellipse, defined as 






