This is an old revision of this page, as edited by 202.63.48.180 (talk) at 11:30, 8 May 2006 (→The argument of EPR). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 11:30, 8 May 2006 by 202.63.48.180 (talk) (→The argument of EPR)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)
The Bohr-Einstein debates is a popular name given to what was actually a series of epistemological challenges presented by Albert Einstein against what has come to be called the standard or Copenhagen interpretation of quantum mechanics. Since Einstein's closest friend and primary interlocutor in the "school" of Copenhagen was the physicist Niels Bohr, and it was Bohr who provided answers to most of the challenges presented by Einstein, what was actually a friendly and fruitful series of exchanges of ideas, has taken on the label of a "debate".
Einstein's position with respect to quantum mechanics is infinitely more subtle and open-minded than it has often been portrayed in technical manuals and popular science articles. This will become clearer during the course of the discussion. Be that as it may, his constant and powerful criticisms of the quantum "orthodoxy” compelled the defenders of that orthodoxy to sharpen and refine their understanding of the philosophical and scientific implications of their own theory.
Einstein's natural reference point, as mentioned above, was always Niels Bohr, as the person who, more than other members of the School of Copenhagen, was animated by a particular interest for the philosophical and epistemological aspects of the theory and drew inspiration from the surprising aspects of the microscopic world in order to present daring hypotheses about reality and about knowledge, such as his idea of complementarity. These two giants of scientific thought nurtured a profound respect for each other and they were both extremely attentive to the acute and penetrating observations of the other. The debate is not only of historical interest: as we will see Einstein's attacks often provoked reactions on the part of Bohr which called into question the crucial elements of the formalization of QM and of its interpretation. This articulated process, in which many other important scientists, from Ehrenfest and Heisenberg to Born and from Schrödinger to John von Neumann, took part, brought more and more detailed attention on certain particularly problematic points of the theory.
First stage
As mentioned above, Einstein's position underwent significant modifications over the course of the years. In the first stage, Einstein refuses to accept quantum indeterminism and seeks to demonstrate that the principle of indeterminacy can be violated, suggesting ingenious gedanken experimente which should permit the simultaneous and arbitrarily accurate determination of incompatible variables, such as position and velocity, or to explicitly reveal simultaneously the wave and the particle aspects of the same process.
The first serious attack by Einstein on the "orthodox" conception took place during the Fifth Conference of Physics at the Solvay Institute in 1927. Einstein pointed out how it was possible to take advantage of the (universally accepted) laws of conservation of energy and of impulse (momentum) in order to obtain information on the state of a particle in a process of interference which, according to the principle of indeterminacy or that of complementarity, should not be accessible.

In order to follow his argumentation and to evaluate Bohr's response, it is convenient to refer to the experimental apparatus illustrated in figure A. A beam of light perpendicular to the X axis which propagates in the direction z encounters a screen S1 which presents a narrow (with respect to the wavelength of the ray) slit. After having passed through the slit, the wave function diffracts with an angular opening that causes it to encounter a second screen S2 which presents two slits. The successive propagation of the wave results in the formation of the interference figure on the final screen F.
At the passage through the two slits of the second screen S2, the wave aspects of the process become essential. In fact, it is precisely the interference between the two terms of the superposition corresponding to states in which the particle is localized in one of the two slits which implies that the particle is "guided" preferably into the zones of constructive interference and cannot end up in a point in the zones of destructive interference (in which the wave function is nullified). It is also important to note that any experiment designed to evidence the "corpuscular" aspects of the process at the passage of the screen S2 (which, in this case, reduces to the determination of which slit the particle has passed through) inevitably destroys the wave aspects, implies the disappearance of the interference figure and the emergence of two concentrated spots of diffraction which confirm our knowledge of the trajectory followed by the particle.
At this point Einstein brings into play the first screen as well and argues as follows: since the incident particles have velocities (practically) perpendicular to the screen S1, and since it is only the interaction with this screen than can cause a deflection from the original direction of propagation, by the law of conservation of impulse which implies that the sum of the impulses of two systems which interact is conserved, if the incident particle is deviated toward the top, the screen will recoil toward the bottom and vice-versa. In realistic conditions the mass of the screen is so heavy that it will remain stationary, but, in principle, it is possible to measure even an infinitesimal recoil. If we imagine taking the measurement of the impulse of the screen in the direction X after every single particle has passed, we can know, from the fact that the screen will be found recoiled toward the top (bottom), if the particle in question has been deviated toward the bottom (top) and therefore we can know from which slit in S2 the particle has passed. But since the determination of the direction of the recoil of the screen after the particle has passed cannot influence the successive development of the process, we will still have an interference figure on the screen F. The interference takes place precisely because the state of the system is the superposition of two states whose wave functions are non-zero only near one of the two slits. On the other hand, if every particle passes through only the slit b or the slit c, then the set of systems is the statistical mixture of the two states, which means that interference is not possible. If Einstein is correct, then there is a violation of the principle of indeterminacy.
Bohr's response was to illustrate Einstein's idea more clearly via the diagrams in Figures B and C. Bohr observes that extremely precise knowledge of any (potential) vertical motion of the screen is an essential presupposition in Einstein's argument. In fact, if its velocity in the direction X before the passage of the particle is not known with a precision substantially greater than that induced by the recoil (that is, if it were already moving vertically with an unknown and greater velocity than that which it derives as a consequence of the contact with the particle), then the determination of its motion after the passage of the particle would not give the information we seek. However, Bohr continues, an extremely precise determination of the velocity of the screen, when one applies the principle of indeterminacy, implies an inevitable imprecision of its position in the direction X. Before the process even begins, the screen would therefore occupy an indeterminate position at least to a certain extent (defined by the formalism). Now consider, for example, the point d in figure A, where there is destructive interference. It's obvious that any displacement of the first screen would make the lengths of the two paths, a-b-d and a-c-d, different from those indicated in the figure. If the difference between the two paths varies by half a wavelength, at point d there will be constructive rather than destructive interference. The ideal experiment must average over all the possible positions of the screen S1, and, for every position, there corresponds, for a certain fixed point F, a different type of interference, from the perfectly destructive to the perfectly constructive. The effect of this averaging is that the pattern of interference on the screen F will be uniformly grey. Once more, our attempt to evidence the corpuscular aspects in S2 has destroyed the possibility of interference in F which depends crucially on the wave aspects.
This argument is correct and convincing. Nevertheless it should be noted that, as Bohr recognized, for the understanding of this phenomenon "it is decisive that, contrary to genuine instruments of measurement, these bodies along with the particles would constitute, in the case under examination, the system to which the quantum-mechanical formalism must apply. With respect to the precision of the conditions under which one can correctly apply the formalism, it is essential to include the entire experimental apparatus. In fact, the introduction of any new apparatus, such as a mirror, in the path of a particle could introduce new effects of interference which influence essentially the predictions about the results which will be registered at the end." Further along, Bohr attempts to resolve this ambiguity concerning which parts of the system should be considered macroscopic and which not:
- In particular, it must be very clear that...the unambiguous use of spatiotemporal concepts in the description of atomic phenomena must be limited to the registration of observations which refer to images on a photographic lens or to analogous practically irreversible effects of amplification such as the formation of a drop of water around an ion in a dark room.
Bohr's argument about the impossibility of using the apparatus proposed by Einstein to violate the principle of indeterminacy depends crucially on the fact that a macroscopic system (the screen S1) obeys quantum laws. On the other hand, Bohr consistently asserted that, in order to illustrate the microscopic aspects of reality it is necessary to set off a process of amplification which involves macroscopic apparatuses, whose fundamental characteristic is that of obeying classical laws and which can be described in classical terms. This ambiguity would later come back in the form of what is still called today the measurement problem.
The principle of indeterminacy applied to time and energy
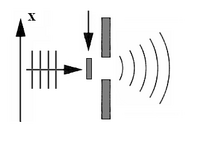
In many textbook examples and popular discussions of quantum mechanics, the principle of indeterminacy is explained by reference to the pair of variables position and velocity (or angular momentum). It is important to note that the wave nature of physical processes implies that there must exist another relation of indeterminacy: that between time and energy. In order to comprehend this relation, it is convenient to refer to the experiment illustrated in Figure D, which results in the preparation of a wave which is limited in spatial extension. Assume that, as illustrated in the figure, a ray which is extremely extended longitudinally is propagated toward a screen with a slit furnished with a shutter which remains open only for a very brief interval of time . Beyond the slit, there will be a wave of limited spatial extension which continues to propagate toward the right.
A perfectly monochromatic wave (such as a note which cannot be divided into harmonics) is infinitely spatially extended. In order to have a wave which is limited in spatial extension (which is technically called a wave packet), several waves of different frequencies must be superimposed and distributed continuously within a certain interval of frequencies around an average value, such as . It then happens that at a certain instant, there exists a spatial region (which translates with time) in which the contributions of the various fields of the superposition add up constructively. Nonetheless, according to a precise mathematical theorem, as we move far away from this region, the phases of the various fields, in any specified point, are distributed casually and destructive interference is produced. The region in which the wave is non-zero is therefore spatially limited. It is easy to demonstrate that if the wave has a spatial extension equal to (which means, in our example, that the shutter has remained open for a time where v is the velocity of the wave), then the wave contains (or is a superposition of) various monochromatic waves whose frequencies cover an interval which satisfies the relation:
Remembering that in the universal relation of Planck, frequency and energy are proportional:
it follows immediately from the preceding inequality that the particle associated with the wave should possess an energy which is not perfectly defined (since different frequencies are involved in the superposition) and consequently there is indeterminacy in energy:
From this it follows immediately that:
>
which is the relation of indeterminacy between time and energy.
Einstein's second attack

At the sixth Congress of Solvay in 1930, the indeterminacy relation just discussed was Einstein's target of attack. His idea contemplates the existence of an experimental apparatus which was subsequently designed by Bohr in such a way as to emphasize the essential elements and the key points which he would use in his response.
Einstein considers a box (figure E) containing electromagnetic radiation and a clock which controls the opening of a shutter which covers a hole made in one of the walls of the box. The shutter uncovers the hole for a temporal interval which can be chosen arbitrarily. During the opening, we are to suppose that a photon, from among those inside the box, escapes through the hole. In this way a wave of limited spatial extension has been created, following the explanation given above. In order to challenge the indeterminacy relation between time and energy, it is necessary to find a way to determine with an adequate precision the energy that the photon has brought with it. At this point, Einstein turns to the celebrated relation between mass and energy of special relativity: . From this it follows that knowledge of the mass of an object provides a precise indication about its energy. The argument is therefore very simple: if one weighs the box before and after the opening of the shutter and if a certain amount of energy has escaped from the box, the box will be lighter. The variation in weight multiplied by will provide precise knowledge of the energy emitted. Moreover, the clock will indicate the precise time at which the event of the particle’s emission took place. Since, in principle, the weight of the box can be determined to an arbitrary degree of accuracy, the energy emitted can be determined with a precision as accurate as one desires. Therefore, the product can be rendered less than what is implied by the principle of indeterminacy.
The idea, like all of those advanced by Einstein, is particularly acute and the argument seemed unassailable. It's important to consider the impact of all of these exchanges on the people involved at the time. Leon Rosenfeld, a scientist who had participated in the Congress, described the event several years later:
- It was a real shock for Bohr...who, at first, could not think of a solution. For the entire evening he was extremely agitated, and he continued passing from one scientist to another, seeking to persuade them that it could not be the case, that it would have been the end of physics if Einstein were right,; but he couldn't come up with any way to resolve the paradox. I will never forget the image of the two antagonists as they left the club: Einstein, with his tall and commanding figure, who walked tranquilly, with a mildly ironic smile, and Bohr who trotted along beside him, full of excitement...The morning after saw the triumph of Bohr.
The "triumph of Bohr" consisted in his demonstrating, once again, that Einstein's subtle argument was not conclusive, but even more so in the way that he arrived at this conclusion by appealing precisely to one of the great ideas of Einstein: the principle of equivalence between gravitational mass and inertial mass. Bohr showed that, in order for Einstein's experiment to function, the box would have to be suspended on a spring in the middle of a gravitational field. In order to obtain a measurement of weight, a pointer would have to be attached to the box which corresponded with the index on a scale. After the release of a photon, weights could be added to the box to restore it to its original position and this would allow us to determine the weight. But in order to return the box to its original position, the box itself would have to be measured. The inevitable uncertainty of the position of the box translates into an uncertainty in the position of the pointer and of the determination of weight and therefore of energy. On the other hand, since the system is immersed in a gravitational field which varies with the position, according to the principle of equivalence the uncertainty in the position of the clock implies an uncertainty with respect to its measurement of time and therefore of the value of the interval . A precise evaluation of this effect leads to the conclusion that the relation , cannot be violated.
Second stage
Main article: Hidden variable theoriesThe second phase of Einstein's "debate" with Bohr and the orthodox interpretation is characterized by an acceptance of the fact that it is, as a practical matter, impossible to simultaneously determine the values of certain incompatible quantities, but the rejection that this implies that these quantities do not actually have precise values. He rejects the probabilistic interpretation of Born and insists that quantum probabilities are epistemic and not ontological in nature. As a consequence, the theory must be incomplete in some way. He recognizes the great value of the theory, but suggests that it "does not tell the whole story," and, while providing an appropriate description at a certain level, it gives no information on the more fundamental underlying level:
- I have the greatest consideration for the goals which are pursued by the physicists of the latest generation which go under the name of quantum mechanics, and I believe that this theory represents a profound level of truth, but I also believe that the restriction to laws of a statistical nature will turn out to be transitory....Without doubt quantum mechanics has grasped an important fragment of the truth and will be a paragon for all future fundamental theories, for the fact that it must be deducible as a limiting case from such foundations, just as electrostatics is deducible from Maxwell's equations of the electromagnetic field or as thermodynamics is deducible from statistical mechanics.
These thoughts of Einstein’s would set off a line of research into so-called hidden variable theories, such as the one formulated by David Bohm, in an attempt to complete the edifice of quantum theory. The impossibility of completing the theory of quantum mechanics was definitively demonstrated by John Stewart Bell with the formulation of Bell's inequality in 1964.
Third stage
| This is an explanatory essay about Error: No page specified. This page provides additional information about concepts in the page(s) it supplements. This page is not one of Misplaced Pages's policies or guidelines as it has not been thoroughly vetted by the community. | Shortcut |
The argument of EPR
In 1935 Einstein, Boris Podolsky and Nathan Rosen developed an argument, published in the magazine Physics Review with the title Is the quantum description of physical reality complete?, based on an entangled state of two particles (a similar argument can be found in the supplement to this section). Before coming to this argument, it is necessary to formulate another hypothesis that comes out of Einstein's work in relativity: the idea of locality. The elements of physical reality which are objectively possessed cannot be influenced instantaneously at a distance.
The argument of EPR can be summarized as follows:
1) Consider a system of two photons which at time t are located, respectively, in the spatially distant regions A and B and which are also in the entangled state of polarization described above:
2) At time t the photon in region A is tested for vertical polarization. Suppose that the result of the measurement is that the photon passes through the filter. According to the reduction of the wave packet, the result is that, at time t+dt, the system becomes:
3) At this point, the observer in A who carried out the first measurement on photon 1, without doing anything else that could disturb the system or the other photon, can predict with certainty that photon 2 will pass a test of vertical polarization. From assumption (R), it follows that photon 2 possesses an element of physical reality: that of having a vertical polarization.
4) According to the assumption of locality, it cannot have been the action carried out in A which created this element of reality for photon 2. Therefore, we must conclude that the photon possessed the property of being able to pass the vertical polarization test before and independently of the measurement of photon 1.
5) At time t, the observer in A could have decided to carry out a test of polarization at 45°, obtaining a certain result, for example, that the photon passes the test. In that case, he could have concluded that photon 2 turned out to be polarized at 45°. Alternatively, if the photon did not pass the test, he could have concluded that photon 2 turned out to be polarized at 135°. Combining one of these alternatives with the conclusion reached in 4, it seems that photon 2, before the measurement took place, possessed both the property of being able to pass with certainty a test of vertical polarization and the property of being able to pass with certainty a test of polarization at either 45° or 135°. These properties are incompatible according to the formalism.
6) Since natural and obvious requirements have forced the conclusion that photon 2 simultaneously possesses incompatible properties, this means that, even if it is not possible to determine these properites simultaneously and with arbitrary precision, they are nevertheless possessed objectively by the system. But quantum mechanics denies this possiblity and it is therefore an incomplete theory.
Bohr's response
Bohr's response to this fascinating and elegant argument was published, five months later than the original publication of EPR, in the same magazine Physical Review and with the exact same title as the original. The crucial point of Bohr's answer is distilled in a passage which he later had republished in Paul Arthur Schilpp's book Albert Einstein, scientist-philosopher in honor of the seventieth birthday of Einstein. Bohr attacks assumption (R) of EPR by stating:
- the statement of the criterion in question is ambiguous with regard to the expression "without disturbing the system in any way". Naturally, in this case no mechanical disturbance of the system under examination can take place in the crucial stage of the process of measurement. But even in this stage there arises the essential problem of an influence on the precise conditions which define the possible types of prediction which regard the subsequent behaviour of the system...their arguments do not justify their conclusion that the quantum description turns out to be essentially incomplete...This description can be characterized as a rational use of the possibilities of an unambiguous interpretation of the process of measurement compatible with the finite and uncontrollable interaction between the object and the instrument of measurement in the context of quantum theory.
As John Bell later pointed out, this passage is almost unintelligible. What does Bohr mean, Bell asks, by the specification "mechanical" that is used to refer to the "disturbances" that Bohr maintains should not be taken into consideration? What is meant by the expression "an influence on the precise conditions" if not that different measurements in A provide different information on the system in B? This fact is not only admitted but is an essential part of the argument of EPR. Lastly, what could Bohr have meant by the expression "uncontrollable interaction between the object and the measuring apparatus", considering that the central point of the argument of EPR is the hypothesis that, if one accepts locality, only the part of the system in A can be disturbed by the process of measurement and that, notwithstanding this fact, this process provides precise information on the part of the system in B? Is Bohr already contemplating the possibility of "spooky action at a distance?" If so, why not declare it explicitly? If one abandons the assumption of non-locality, the argument of EPR obviously collapses immediately. But the fact that non-locality is intrinsic to the quantum universe was demonstrated thirty years later by Bell, so this seems extremely unlikely.
In any case, very few among the illustrious protagonists of the debate on the foundations of quantum theory were able to grasp the true sense of the profound analysis of Einstein. Pauli dismissed it with a few words and Born completely misinterpreted it. But Einstein's defeat (and it really was a defeat) represents one of the highest points of scientific research in the first half of the twentieth century because it called attention to an element of reality, quantum non-locality, which is absolutely central to our modern understanding of the physical world.
Fourth stage
In his last writing on the topic, Einstein further refined his position, making it completely clear that what really disturbed him about the quantum theory was the problem of the total renunciation of all minimal standards of realism, even at the macroscopic level, that the acceptance of the completeness of the theory implied. Although the majority of experts in the field seem to accept the Copenhagen interpretation, there are a growing number of critics who, like Einstein, believe that it has failed to provide a sensible and acceptable representation of reality (see Interpretation of quantum mechanics).
See also
- Afshar's experiment
- Complementarity
- Copenhagen interpretation
- EPR paradox
- Quantum eraser
- Schrödinger's cat
- Uncertainty principle
- Wheeler's delayed choice experiment
References
- Boniolo, G., (1997) Filosofia della Fisica, Mondadori, Milan.
- Born, M. (1973) The Born Einstein Letters, Walker and Company, New York, 1971.
- Ghirardi, Giancarlo, (1997) Un Occhiata alle Carte di Dio, Il Saggiatore, Milan.
- Pais, A., (1986) Subtle is the Lord... The Science and Life of Albert Einstein, Oxford University Press, Oxford, 1982.
- Shilpp, P.A., (1958) Albert Einstein: Philosopher-Scientist, Northwestern University and Southern Illinois University, Open Court, 1951.
 . Beyond the slit, there will be a wave of limited spatial extension which continues to propagate toward the right.
. Beyond the slit, there will be a wave of limited spatial extension which continues to propagate toward the right.
 .
It then happens that at a certain instant, there exists a spatial region (which translates with time) in which the contributions of the various fields of the superposition add up constructively. Nonetheless, according to a precise mathematical theorem, as we move far away from this region, the
.
It then happens that at a certain instant, there exists a spatial region (which translates with time) in which the contributions of the various fields of the superposition add up constructively. Nonetheless, according to a precise mathematical theorem, as we move far away from this region, the  (which means, in our example, that the shutter has remained open for a time
(which means, in our example, that the shutter has remained open for a time  where v is the velocity of the wave), then the wave contains (or is a superposition of) various monochromatic waves whose frequencies cover an interval
where v is the velocity of the wave), then the wave contains (or is a superposition of) various monochromatic waves whose frequencies cover an interval  which satisfies the relation:
which satisfies the relation:



 >
> . From this it follows that knowledge of the mass of an object provides a precise indication about its energy. The argument is therefore very simple: if one weighs the box before and after the opening of the shutter and if a certain amount of energy has escaped from the box, the box will be lighter. The variation in weight multiplied by
. From this it follows that knowledge of the mass of an object provides a precise indication about its energy. The argument is therefore very simple: if one weighs the box before and after the opening of the shutter and if a certain amount of energy has escaped from the box, the box will be lighter. The variation in weight multiplied by  will provide precise knowledge of the energy emitted.
Moreover, the clock will indicate the precise time at which the event of the particle’s emission took place. Since, in principle, the weight of the box can be determined to an arbitrary degree of accuracy, the energy emitted can be determined with a precision
will provide precise knowledge of the energy emitted.
Moreover, the clock will indicate the precise time at which the event of the particle’s emission took place. Since, in principle, the weight of the box can be determined to an arbitrary degree of accuracy, the energy emitted can be determined with a precision  as accurate as one desires. Therefore, the product
as accurate as one desires. Therefore, the product  can be rendered less than what is implied by the principle of indeterminacy.
can be rendered less than what is implied by the principle of indeterminacy.
 , cannot be violated.
, cannot be violated.
 described above:
described above:

