Misplaced Pages

This is an old revision of this page, as edited by 72.10.105.229 (talk) at 13:39, 27 April 2007 (→See also). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

This article is about Euler's formula in complex analysis. For Euler's formula in graph theory see planar graph. See also topics named after Euler.

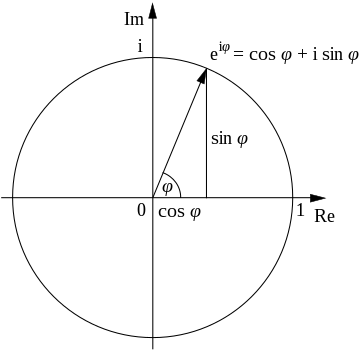
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that shows a deep relationship between the trigonometric functions and the complex exponential function. (Euler's identity is a special case of the Euler formula.)

Euler's formula states that, for any real number x,

${\displaystyle e^{ix}=\cos(x)+i\sin(x)\!}$

where

${\displaystyle e\,}$ is the base of the natural logarithm

${\displaystyle i\,}$ is the imaginary unit

${\displaystyle \cos()\,}$ and ${\displaystyle \sin()\,}$ are trigonometric functions.

Richard Feynman called Euler's formula "our jewel" and "the most remarkable formula in mathematics".

History

Euler's formula was proven for the first time by Roger Cotes in 1714 in the form ln(cos(x) + i sin(x)) = ix (where "ln" means natural logarithm, i.e. log to base e). It was Euler who published the equation in its current form in 1748, basing his proof on the infinite series of both sides being equal. Neither of these men saw the geometrical interpretation of the formula: the view of complex numbers as points in the complex plane arose only some 50 years later (see Caspar Wessel).

Applications in complex number theory

This formula can be interpreted as saying that the function e traces out the unit circle in the complex number plane as x ranges through the real numbers. Here, x is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counter clockwise and in radians. The formula is valid only if sin and cos take their arguments in radians rather than in degrees.

The original proof is based on the Taylor series expansions of the exponential function e (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers z.

Euler's formula can be used to represent complex numbers in polar coordinates. Any complex number z = x + iy can be written as

${\displaystyle z=x+iy=|z|(\cos \phi +i\sin \phi )=|z|e^{i\phi }\,}$

${\displaystyle {\bar {z}}=x-iy=|z|(\cos \phi -i\sin \phi )=|z|e^{-i\phi }\,}$

where

${\displaystyle x=\mathrm {Re} \{z\}\,}$ the real part

${\displaystyle y=\mathrm {Im} \{z\}\,}$ the imaginary part

${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}}$ the magnitude of z

and ${\displaystyle \phi \,}$ is the argument of z— the angle between the x axis and the vector z measured counterclockwise and in radians — which is defined up to addition of 2π.

Now, taking this derived formula, we can use Euler's formula to define the logarithm of a complex number. To do this, we also use the facts that

${\displaystyle a=e^{ln(a)}\,}$

and

${\displaystyle e^{a}e^{b}=e^{a+b}\,}$

both valid for any complex numbers a and b.

Therefore, one can write:

${\displaystyle z=|z|e^{i\phi }=e^{\ln |z|}e^{i\phi }=e^{\ln |z|+i\phi }\,}$

for any ${\displaystyle z\neq 0}$. Taking the logarithm of both sides shows that:

${\displaystyle \ln z=\ln |z|+i\phi .\,}$

and in fact this can be used as the definition for the complex logarithm. The logarithm of a complex number is thus a multi-valued function, due to the fact that ${\displaystyle \phi \,}$ is multi-valued.

Finally, the other exponential law

${\displaystyle (e^{a})^{k}=e^{ak},\,}$

which can be seen to hold for all integers k, together with Euler's formula, implies several trigonometric identities as well as de Moivre's formula.

Relationship to trigonometry

Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:

${\displaystyle \cos x={e^{ix}+e^{-ix} \over 2}}$

${\displaystyle \sin x={e^{ix}-e^{-ix} \over 2i}}$

The two equations above can be derived by adding or subtracting Euler's formulas:

${\displaystyle e^{ix}=\cos x+i\sin x\;}$

${\displaystyle e^{-ix}=\cos x-i\sin x\;}$

and solving for either cosine or sine.

These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:

${\displaystyle \cos(iy)={e^{-y}+e^{y} \over 2}=\cosh(y)}$

${\displaystyle \sin(iy)={e^{-y}-e^{y} \over 2i}=i\sinh(y).}$

Other applications

In differential equations, the function e is often used to simplify derivations, even if the final answer is a real function involving sine and cosine. Euler's identity is an easy consequence of Euler's formula.

In electrical engineering and other fields, signals that vary periodically over time are often described as a combination of sine and cosine functions (see Fourier analysis), and these are more conveniently expressed as the real part of exponential functions with imaginary exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.

Proofs

Using Taylor series

Here is a proof of Euler's formula using Taylor series expansions as well as basic facts about the powers of i:

${\displaystyle {\begin{aligned}i^{0}&{}=1,\quad &i^{1}&{}=i,\quad &i^{2}&{}=-1,\quad &i^{3}&{}=-i,\\i^{4}&={}1,\quad &i^{5}&={}i,\quad &i^{6}&{}=-1,\quad &i^{7}&{}=-i,\\\end{aligned}}}$

and so on. The functions e, cos(x) and sin(x) (assuming x is real) can be expressed using their Taylor expansions around zero:

${\displaystyle {\begin{aligned}e^{x}&{}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots \\\cos x&{}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\\sin x&{}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \end{aligned}}}$

For complex z we define each of these function by the above series, replacing x with z. This is possible because the radius of convergence of each series is infinite. We then find that

${\displaystyle {\begin{aligned}e^{iz}&{}=1+iz+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+{\frac {(iz)^{5}}{5!}}+{\frac {(iz)^{6}}{6!}}+{\frac {(iz)^{7}}{7!}}+{\frac {(iz)^{8}}{8!}}+\cdots \\&{}=1+iz-{\frac {z^{2}}{2!}}-{\frac {iz^{3}}{3!}}+{\frac {z^{4}}{4!}}+{\frac {iz^{5}}{5!}}-{\frac {z^{6}}{6!}}-{\frac {iz^{7}}{7!}}+{\frac {z^{8}}{8!}}+\cdots \\&{}=\left(1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+{\frac {z^{8}}{8!}}-\cdots \right)+i\left(z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+\cdots \right)\\&{}=\cos(z)+i\sin(z)\end{aligned}}}$

The rearrangement of terms is justified because each series is absolutely convergent. Taking z = x to be a real number gives the original identity as Euler discovered it.

Using calculus

Define the function ${\displaystyle f\ }$ by

${\displaystyle f(x)={\frac {\cos x+i\sin x}{e^{ix}}}.\ }$

This is allowed since the equation

${\displaystyle e^{ix}\cdot e^{-ix}=e^{0}=1\ }$

implies that ${\displaystyle e^{ix}\ }$ is never zero.

The derivative of ${\displaystyle f\ }$ is, according to the quotient rule:

${\displaystyle {\begin{aligned}f'(x)&{}={\frac {(-\sin x+i\cos x)\cdot e^{ix}-(\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^{2}}}\\&{}={\frac {-\sin x\cdot e^{ix}-i^{2}\sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&{}={\frac {(-1-i^{2})\cdot \sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&{}={\frac {(-1-(-1))\cdot \sin x\cdot e^{ix}}{(e^{ix})^{2}}}\\&{}=0.\end{aligned}}}$

Therefore, ${\displaystyle f\ }$ must be a constant function. Thus,

${\displaystyle {\frac {\cos x+i\sin x}{e^{ix}}}=f(x)=f(0)={\frac {\cos 0+i\sin 0}{e^{0}}}=1.}$

Rearranging,

${\displaystyle \displaystyle \cos x+i\sin x=e^{ix}.}$

Q.E.D.

Using ordinary differential equations

Define the function g(x) by

${\displaystyle g(x)\ {\stackrel {\mathrm {def} }{=}}\ e^{ix}.\ }$

Considering that i is constant, the first and second derivatives of g(x) are

${\displaystyle g'(x)=ie^{ix}\ }$

${\displaystyle g''(x)=i^{2}e^{ix}=-e^{ix}\ }$

because i = −1 by definition. From this the following 2-order linear ordinary differential equation is constructed:

${\displaystyle g''(x)=-g(x)\ }$

or

${\displaystyle g''(x)+g(x)=0.\ }$

Being a 2-order differential equation, there are two linearly independent solutions that satisfy it:

${\displaystyle g_{1}(x)=\cos(x)\ }$

${\displaystyle g_{2}(x)=\sin(x).\ }$

Both cos(x) and sin(x) are real functions in which the 2 derivative is identical to the negative of that function. Any linear combination of solutions to a homogeneous differential equation is also a solution. Then, in general, the solution to the differential equation is

${\displaystyle g(x)\,}$	${\displaystyle =Ag_{1}(x)+Bg_{2}(x)\ }$
	${\displaystyle =A\cos(x)+B\sin(x)\ }$

for any constants A and B. But not all values of these two constants satisfy the known initial conditions for g(x):

${\displaystyle g(0)=e^{i0}=1\ }$

${\displaystyle g'(0)=ie^{i0}=i\ }$.

However these same initial conditions (applied to the general solution) are

${\displaystyle g(0)=A\cos(0)+B\sin(0)=A\ }$

${\displaystyle g'(0)=-A\sin(0)+B\cos(0)=B\ }$

resulting in

${\displaystyle g(0)=A=1\ }$

${\displaystyle g'(0)=B=i\ }$

and, finally,

${\displaystyle g(x)\ {\stackrel {\mathrm {def} }{=}}\ e^{ix}=\cos(x)+i\sin(x).\ }$

Q.E.D.

See also

• Leonhard Euler
• Euler's identity
• Complex number
• Exponentiation
• Exponential function
• Trigonometry

blah blah

References

1. Feynman, Richard P. (1977). The Feynman Lectures on Physics, vol. I. Addison-Wesley. pp. p. 22-10. ISBN 0-201-02010-6. {{cite book}}: |pages= has extra text (help)
2. John Stillwell (2002). Mathematics and Its History. Springer.

External links

• Proof of Euler's Formula by Julius O. Smith III
• Euler's Formula and Fermat's Last Theorem
• Complex Exponential Function Module by John H. Mathews

• Complex analysis
• Mathematical theorems
• Trigonometry