This is an old revision of this page, as edited by FDT (talk | contribs) at 07:56, 26 April 2008 (It's not apparent. The effect can be viewed from the inertial frame. We can see the cyclones from space). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 07:56, 26 April 2008 by FDT (talk | contribs) (It's not apparent. The effect can be viewed from the inertial frame. We can see the cyclones from space)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)
The Coriolis effect is a deflection of moving objects from a straight path when they move in a rotating frame of reference. The effect is named after Gaspard-Gustave Coriolis, a French scientist who described it in 1835, though the mathematics appeared in the tidal equations of Pierre-Simon Laplace in 1778. Sometimes this force is called a fictitious force (or pseudo force), because it does not appear when the motion is expressed in an inertial frame of reference, in which the motion of an object is explained by the real impressed forces, together with inertia. In a rotating frame, the Coriolis force, which depends on the velocity of the moving object, and centrifugal force, which does not, are needed in the equation to correctly describe the motion.
Perhaps the most commonly encountered rotating reference frame is the Earth. Freely moving objects on the surface of the Earth experience a Coriolis force, and appear to veer to the right in the northern hemisphere, and to the left in the southern. Movements of air in the atmosphere and water in the ocean are notable examples of this behavior: rather than flowing directly from areas of high pressure to low pressure, as they would on a non-rotating planet, winds and currents tend to flow to the right (left) of this direction north (south) of the equator. This effect is responsible for the rotation of large cyclones (see Coriolis in meteorology).
Formula
In non-vector terms: at a given rate of rotation of the observer, the magnitude of the Coriolis acceleration of the object is proportional to the velocity of the object and also to the sine of the angle between the direction of movement of the object and the axis of rotation.
The vector formula for the magnitude and direction the Coriolis acceleration is
where (here and below) is the velocity of the particle in the rotating system, and is the angular velocity vector (which has magnitude equal to the rotation rate and is directed along the axis of rotation) of the rotating system. The equation may be multiplied by the mass of the relevant object to produce the Coriolis force:
- .
See fictitious force for a derivation.
The × symbols represent cross products. (The cross product does not commute: changing the order of the vectors changes the sign of the product.)
The Coriolis effect is the behavior added by the Coriolis acceleration. The formula implies that the Coriolis acceleration is perpendicular both to the direction of the velocity of the moving mass and to the rotation axis. So in particular:
- if the velocity is parallel to the rotation axis, the Coriolis acceleration is zero
- if the velocity is straight inward to the axis, the acceleration is in the direction of local rotation
- if the velocity is straight outward from the axis, the acceleration is against the direction of local rotation
- if the velocity is in the direction of local rotation, the acceleration is outward from the axis
- if the velocity is against the direction of local rotation, the acceleration is inward to the axis
For example, consider a location with latitude on a sphere that is rotating around the north-south axis. A local coordinate system is set up with the axis horizontally due east, the axis horizontally due north and the axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system are:
- , ,
When considering atmospheric or oceanic dynamics, the vertical velocity is small and the vertical component of the Coriolis acceleration is small compared to gravity. The restriction of the above to the horizontal plane is (with ):
- , , where is called the Coriolis parameter.
From this it can be immediately seen that (for positive and ) a movement due east results in a force due south and a movement due north in a force due east — both turned 90° to the right.
Causes
The Coriolis effect exists only when using a rotating reference frame. It is mathematically deduced from the law of inertia. Hence it does not correspond to any actual acceleration or force, but only the appearance thereof from the point of view of a rotating system.
The Coriolis effect exhibited by a moving object can be interpreted as being the sum of the effects of two different causes of equal magnitude.
The first cause is the change of the velocity of an object in time. The same velocity (in an inertial frame of reference where the normal laws of physics apply) will be seen as different velocities at different times in a rotating frame of reference. The apparent acceleration is proportional to the angular velocity of the reference frame (the rate at which the coordinate axes changes direction), and to the velocity of the object. This gives a term . The minus sign arises from the traditional definition of the cross product (right hand rule), and from the sign convention for angular velocity vectors.
The second cause is change of velocity in space. Different points in a rotating frame of reference have different velocities (as seen from an inertial frame of reference). In order for an object to move in a straight line it must therefore be accelerated so that its velocity changes from point to point by the same amount as the velocities of the frame of reference. The effect is proportional to the angular velocity (which determines the relative speed of two different points in the rotating frame of reference), and the velocity of the object perpendicular to the axis of rotation (which determines how quickly it moves between those points). This also gives a term .
Common misconceptions about the Coriolis Effect
- The Coriolis effect is not a result of the curvature of the Earth, only of its rotation. (However, the value of the Coriolis parameter, , does vary with latitude, and that dependence is due to the Earth's shape.)
- The fact that ballistic missiles and satellites appear to follow curved paths when plotted on common world maps is mainly due to the fact that the earth is spherical and the shortest distance between two points on the earth's surface (called a great circle) is usually not a straight line on those maps. Every two-dimensional (flat) map necessarily distorts the earth's curved (three-dimensional) surface in some way. Typically (as in the commonly used Mercator projection, for example), this distortion increases with proximity to the poles. In the northern hemisphere for example, a ballistic missile fired toward a distant target using the shortest possible route (a great circle) will appear on such maps to follow a path north of the straight line from target to destination, and then curve back toward the equator. This occurs because the latitudes, which are projected as straight horizontal lines on most world maps, are in fact circles on the surface of a sphere, which get smaller as they get closer to the pole. Being simply a consequence of the sphericity of the Earth, this would be true even if the Earth didn't rotate. The Coriolis effect is of course also present, but its effect on the plotted path is much smaller.
- The Coriolis force should not be confused with the centrifugal force given by . A rotating frame of reference will always cause a centrifugal force no matter what the object is doing (unless that body is particle-like and lies on the axis of rotation), whereas the Coriolis force requires the object to be in motion relative to the rotating frame with a velocity that is not parallel to the rotation axis. Because the centrifugal force always exists, it can be easy to confuse the two, making simple explanations of the effect of Coriolis in isolation difficult. In particular, when is tangential to a circle centered on and perpendicular to the axis of rotation, the Coriolis force is parallel to the centrifugal force. It is then possible to construct a rotating reference frame of a different rotational speed, where is zero and there is no Coriolis force.
Visualization of the Coriolis effect


Left: the motion as observed from the inertial point of view. The gravitational force pulling the object toward the bottom (center) of the dish is proportional to the distance of the object from the center. This force causes the elliptical motion.
Right: the motion as seen from a co-rotating point of view. In this frame, the inward gravitational force is balanced by the outward centrifugal force. The only unbalanced force is Coriolis, and the motion is an inertial circle.
To demonstrate the Coriolis effect, a parabolic turntable can be used. On a flat turntable, the inertia of a co-rotating object would force it off the edge. But if the surface of the turntable has the correct parabolic bowl shape and is rotated at the correct rate, then the component of gravity tangential to the bowl surface will exactly equal the centripetal force necessary to keep the water rotating at its velocity and radius of curvature. This allows the Coriolis force to be displayed in isolation. When a container of fluid is rotating on a turntable, the surface of the fluid naturally assumes the correct parabolic shape. This fact may be exploited to make a parabolic turntable by using a fluid that sets after several hours, such as a synthetic resin.
Discs cut from cylinders of dry ice can be used as pucks, moving around almost frictionlessly over the surface of the parabolic turntable, allowing effects of Coriolis on dynamic phenomena to show themselves. To get a view of the motions as seen from the reference frame rotating with the turntable, a video camera is attached to the turntable so as to co-rotate with the turntable. Because this reference frame rotates several times a minute, rather than only once a day like the Earth, the Coriolis acceleration produced is many times larger, and so easier to observe on small time and spatial scales, than is the Coriolis acceleration caused by the rotation of the Earth.
In a manner of speaking, the Earth is analogous such a turntable. The rotation has caused the planet to settle on a spheroid shape such that the normal force, the gravitational force, and the centrifugal force exactly balance each other on a "horizontal" surface. (See equatorial bulge.)
The Coriolis effect caused by the rotation of the Earth can be seen indirectly through the motion of a Foucault pendulum.
Draining in bathtubs and toilets
A misconception in popular culture is that water in bathtubs or toilets always drains in one direction in the Northern Hemisphere, and in the other direction in the Southern Hemisphere as a consequence of the Coriolis effect. This idea has been perpetuated by several television programs, including an episode of The Simpsons and one of The X-Files. In addition, several science broadcasts and publications (including at least one college-level physics textbook) have made this incorrect statement.
Some sources that incorrectly attribute draining direction to the Coriolis force also get the direction wrong. If the Coriolis force were the dominant factor, drain vortices would spin counterclockwise in the northern hemisphere and clockwise in the southern.
In reality the Coriolis effect is a few orders of magnitude smaller than various random influences on drain direction, such as the geometry of the container and the direction in which water was initially added to it. Most toilets flush in only one direction, because the toilet water flows into the bowl at an angle. If water shot into the basin from the opposite direction, the water would spin in the opposite direction.
When the water is being drawn towards the drain, the radius of its rotation around the drain decreases, so its rate of rotation increases from the low background level to a noticeable spin in order to conserve its angular momentum (the same effect as ice skaters bringing their arms in to cause them to spin faster). As shown by Ascher Shapiro in a 1961 educational video (Vorticity, Part 1), this effect can indeed reveal the influence of the Coriolis force on drain direction, but only under carefully controlled laboratory conditions. In a large, circular, symmetrical container (ideally over 1m in diameter and conical), still water (whose motion is so little that over the course of a day, displacements are small compared to the size of the container) escaping through a very small hole, will drain in a cyclonic fashion: counterclockwise in the Northern hemisphere and clockwise in the Southern hemisphere—the same direction as the Earth rotates with respect to the corresponding pole.
Coriolis in meteorology

Perhaps the most important instance of the Coriolis effect is in the large-scale dynamics of the oceans and the atmosphere. In meteorology, it is convenient to use a rotating frame of reference where the Earth is stationary. The fictitious centrifugal and Coriolis forces must then be introduced. The former, however, is cancelled by the non-spherical shape of the earth (see the turntable analogy above). Hence the Coriolis force is the only fictitious force to have a significant impact on calculations.
Flow around a low-pressure area
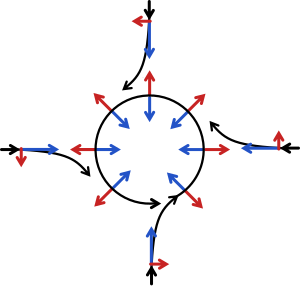
If a low-pressure area forms in the atmosphere, air will tend to flow in towards it, but will be deflected perpendicular to its velocity by the Coriolis acceleration. A system of equilibrium can then establish itself creating circular movement, or a cyclonic flow. The force balance is largely between the pressure gradient force acting towards the low-pressure area and the Coriolis force acting away from the center of the low pressure.
Instead of flowing down the gradient, large scale motions in the atmosphere and ocean tend to occur perpendicular to the pressure gradient. This is known as geostrophic flow. On a non-rotating planet fluid would flow along the straightest possible line, quickly eliminating pressure gradients. Note that the geostrophic balance is thus very different from the case of "inertial motions" (see below) which explains why mid-latitude cyclones are larger by an order of magnitude than inertial circle flow would be.
This pattern of deflection, and the direction of movement, is called Buys-Ballot's law. In the atmosphere, the pattern of flow is called a cyclone. In the Northern Hemisphere the direction of movement around a low-pressure area is counterclockwise. In the Southern Hemisphere, the direction of movement is clockwise because the rotational dynamics is a mirror image there. At high altitudes, outward-spreading air rotates in the opposite direction. Cyclones cannot form on the equator, because in the equatorial region the Coriolis parameter is small.
Inertial circles

An air or water mass moving with speed subject only to the Coriolis force travels in a circular trajectory called an 'inertial circle'. Since the force is directed at right angles to the motion of the particle, it will move with a constant speed, and perform a complete circle with frequency . The magnitude of the Coriolis force also determines the radius of this circle:
- .
On the Earth, a typical mid-latitude value for is 10 s; hence for a typical atmospheric speed of 10 m/s the radius is 100 km, with a period of about 14 hours. In the ocean, where a typical speed is closer to 10 cm/s, the radius of an inertial circle is 1 km. These inertial circles are clockwise in the northern hemisphere (where trajectories are bent to the right) and anti-clockwise in the southern hemisphere.
If the rotating system is a parabolic turntable, then is constant and the trajectories are exact circles. On a rotating planet, varies with latitude and the paths of particles do not form exact circles. Since the parameter varies as the sine of the latitude, the radius of the oscillations associated with a given speed are smallest at the poles (latitude = ±90°), and increase toward the equator.
Length scales and the Rossby number
Further information: Rossby numberThe time, space and velocity scales are important in determining the importance of the Coriolis effect. Whether rotation is important in a system can be determined by its Rossby number, which is the ratio of the velocity, , of a system to the product of the Coriolis parameter, , and the length scale, , of the motion:
- .
A small Rossby number signifies a system which is strongly affected by rotation, and a large Rossby number signifies a system in which rotation is unimportant.
An atmospheric system moving at U = 10 m/s occupying a spatial distance of L = 1000 km, has a Rossby number of approximately 0.1. A man playing catch may throw the ball at U = 30 m/s in a garden of length L = 50 m. The Rossby number in this case would be about = 6000. Needless to say, one does not worry about which hemisphere one is in when playing catch in the garden. However, an unguided missile obeys exactly the same physics as a baseball, but may travel far enough and be in the air long enough to notice the effect of Coriolis. Long-range shells in the Northern Hemisphere landed close to, but to the right of, where they were aimed until this was noted. (Those fired in the southern hemisphere landed to the left.)
The Rossby number can also tell us about the bathtub. If the length scale of the tub is about L = 1 m, and the water moves towards the drain at about U = 60 cm/s, then the Rossby number is about 6 000. Thus, the bathtub is, in terms of scales, much like a game of catch, and rotation is likely to be unimportant.
Other terrestrial effects
The Coriolis effect strongly affects the large-scale oceanic and atmospheric circulation, leading to the formation of robust features like jet streams and western boundary currents. Such features are in geostrophic balance, meaning that the Coriolis and pressure gradient forces balance each other. Coriolis acceleration is also responsible for the propagation of many types of waves in the ocean and atmosphere, including Rossby waves and Kelvin waves. It is also instrumental in the so-called Ekman dynamics in the ocean, and in the establishment of the large-scale ocean flow pattern called the Sverdrup balance.
Other aspects of the Coriolis effect
The practical impact of the Coriolis effect is mostly caused by the horizontal acceleration component produced by horizontal motion.
There are other components of the Coriolis effect. Eastward-traveling objects will be deflected upwards (feel lighter), while westward-traveling objects will be deflected downwards (feel heavier). This is known as the Eötvös effect. This aspect of the Coriolis effect is greatest near the equator. The force produced by this effect is similar to the horizontal component, but the much larger vertical forces due to gravity and pressure mean that it is generally unimportant dynamically.
In addition, objects traveling upwards or downwards will be deflected to the west or east respectively. This effect is also the greatest near the equator. Since vertical movement is usually of limited extent and duration, the size of the effect is smaller and requires precise instruments to detect.
Coriolis elsewhere
Coriolis flow meter
A practical application of the Coriolis effect is the mass flow meter, an instrument that measures the mass flow rate and density of a fluid flowing through a tube. The operating principle, introduced in 1977 by Micro Motion Inc., involves inducing a vibration of the tube through which the fluid passes. The vibration, though it is not completely circular, provides the rotating reference frame which gives rise to the Coriolis effect. While specific methods vary according to the design of the flow meter, sensors monitor and analyze changes in frequency, phase shift, and amplitude of the vibrating flow tubes. The changes observed represent the mass flow rate and density of the fluid.
Molecular physics
In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. Coriolis effects will therefore be present and will cause the atoms to move in a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibrational levels.
Ballistics
The Coriolis effects became important in external ballistics for calculating the trajectories of very long-range artillery shells. The most famous historical example was the Paris gun, used by the Germans during World War I to bombard Paris from a range of about 120 km (75 mi).
Insect flight
Flies (Diptera) and moths (Lepidoptera) utilize the Coriolis effect when flying: their halteres, or antennae in the case of moths, oscillate rapidly and are used as vibrational gyroscopes. See Coriolis effect in insect stability. In this context, the Coriolis effect has nothing to do with the rotation of the Earth.
See also
References
| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (February 2008) (Learn how and when to remove this message) |
Physics and meteorology references
- Coriolis, G.G., 1832: Mémoire sur le principe des forces vives dans les mouvements relatifs des machines. Journal de l'école Polytechnique, Vol 13, 268–302.
(Original article , PDF-file, 1.6 MB, scanned images of complete pages.) - Coriolis, G.G., 1835: Mémoire sur les équations du mouvement relatif des systèmes de corps. Journal de l'école Polytechnique, Vol 15, 142–154
(Original article PDF-file, 400 KB, scanned images of complete pages.) - Gill, AE Atmosphere-Ocean dynamics, Academic Press, 1982.
- Durran, D. R., 1993: Is the Coriolis force really responsible for the inertial oscillation?, Bull. Amer. Meteor. Soc., 74, 2179–2184; Corrigenda. Bulletin of the American Meteorological Society, 75, 261
- Durran, D. R., and S. K. Domonkos, 1996: An apparatus for demonstrating the inertial oscillation, Bulletin of the American Meteorological Society, 77, 557–559.
- Marion, Jerry B. 1970, Classical Dynamics of Particles and Systems, Academic Press.
- Persson, A., 1998 How do we Understand the Coriolis Force? Bulletin of the American Meteorological Society 79, 1373–1385.
- Symon, Keith. 1971, Mechanics, Addison-Wesley
- Phillips, Norman A., 2000 An Explication of the Coriolis Effect, Bulletin of the American Meteorological Society: Vol. 81, No. 2, pp. 299–303.
Historical references
- Grattan-Guinness, I., Ed., 1994: Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. Vols. I and II. Routledge, 1840 pp.
1997: The Fontana History of the Mathematical Sciences. Fontana, 817 pp. 710 pp. - Khrgian, A., 1970: Meteorology—A Historical Survey. Vol. 1. Keter Press, 387 pp.
- Kuhn, T. S., 1977: Energy conservation as an example of simultaneous discovery. The Essential Tension, Selected Studies in Scientific Tradition and Change, University of Chicago Press, 66–104.
- Kutzbach, G., 1979: The Thermal Theory of Cyclones. A History of Meteorological Thought in the Nineteenth Century. Amer. Meteor. Soc., 254 pp.
Footnotes
- "X-Files coriolis error leaves viewers wondering" from Skeptical Inquirer
- "Bad Coriolis" from Penn State College of Earth and Mineral Sciences
- "Who Knew? The No-Spin Zone" from Berkeley Science Review (PDF)
- "Flush Bosh" from snopes.com
- Cloud Spirals and Outflow in Tropical Storm Katrina from Earth Observatory (NASA)
- "Antennae as Gyroscopes", Science, Vol. 315, 9 Feb 2007, p. 771
External links
- The definition of the Coriolis effect from the Glossary of Meteorology
- The Coriolis Effect PDF-file. 17 pages. A general discussion by Anders Persson of various aspects of the coriolis effect, including Foucault's Pendulum and Taylor columns.
- Anders Persson The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885 History of Meteorology 2 (2005)
- Coriolis Force - from ScienceWorld
- The Coriolis Effect: An Introduction. Details of the causes of prevailing wind patterns. Targeted towards ages 5 to 18.
- Coriolis Effect and Drains An article from the NEWTON web site hosted by the Argonne National Laboratory.
- Do bathtubs drain counterclockwise in the Northern Hemisphere? by Cecil Adams.
- Bad Coriolis. An article uncovering misinformation about the Coriolis effect. By Alistair B. Fraser, Emeritus Professor of Meteorology at Pennsylvania State University
- Getting Around The Coriolis Force, an intuitive explanation
- Observe an animation of the Coriolis effect over Earth's surface
- Animation clip showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.
 North Atlantic
North Atlantic gyre North Atlantic
gyre North Atlantic
gyre Indian
Ocean
gyre North
Pacific
gyre South
Pacific
gyre South Atlantic
gyre
 World map of the five major ocean gyres
Categories:
World map of the five major ocean gyres
Categories:

 is the velocity of the particle in the rotating system, and
is the velocity of the particle in the rotating system, and  is the angular velocity vector (which has magnitude equal to the rotation rate and is directed along the axis of rotation) of the rotating system. The equation may be multiplied by the mass of the relevant object to produce the Coriolis force:
is the angular velocity vector (which has magnitude equal to the rotation rate and is directed along the axis of rotation) of the rotating system. The equation may be multiplied by the mass of the relevant object to produce the Coriolis force:
 .
. on a sphere that is rotating around the north-south axis. A local coordinate system is set up with the
on a sphere that is rotating around the north-south axis. A local coordinate system is set up with the  axis horizontally due east, the
axis horizontally due east, the  axis horizontally due north and the
axis horizontally due north and the  axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system are:
axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system are:
 ,
,  ,
, 
 ):
):
 ,
,  , where
, where  is called the
is called the  ) a movement due east results in a force due south and a movement due north in a force due east — both turned 90° to the right.
) a movement due east results in a force due south and a movement due north in a force due east — both turned 90° to the right.
 .
The minus sign arises from the traditional definition of the cross product (
.
The minus sign arises from the traditional definition of the cross product ( , does vary with latitude, and that dependence is due to the Earth's shape.)
, does vary with latitude, and that dependence is due to the Earth's shape.) . A
. A  is tangential to a circle centered on and perpendicular to the axis of rotation, the Coriolis force is parallel to the centrifugal force. It is then possible to construct a rotating reference frame of a different rotational speed, where
is tangential to a circle centered on and perpendicular to the axis of rotation, the Coriolis force is parallel to the centrifugal force. It is then possible to construct a rotating reference frame of a different rotational speed, where  subject only to the Coriolis force travels in a circular trajectory called an 'inertial circle'. Since the force is directed at right angles to the motion of the particle, it will move with a constant speed, and perform a complete circle with frequency
subject only to the Coriolis force travels in a circular trajectory called an 'inertial circle'. Since the force is directed at right angles to the motion of the particle, it will move with a constant speed, and perform a complete circle with frequency  . The magnitude of the Coriolis force also determines the radius of this circle:
. The magnitude of the Coriolis force also determines the radius of this circle:
 .
. , of a system to the product of the Coriolis parameter,
, of a system to the product of the Coriolis parameter,  , of the motion:
, of the motion:
 .
.