Misplaced Pages

This is an old revision of this page, as edited by 142.214.113.96 (talk) at 15:34, 24 February 2006 (→Perceptions of the identity). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

For other meanings, see Euler function (disambiguation)

In mathematical analysis, Euler's identity is the equation

${\displaystyle e^{i\pi }+1=0,\,\!}$

where

${\displaystyle e\,\!}$ is Euler's number, the base of the natural logarithm,

${\displaystyle i\,\!}$ is the imaginary unit, one of the two complex numbers whose square is negative one (the other is ${\displaystyle -i\,\!}$), and

${\displaystyle \pi \,\!}$ is Pi, the ratio of the circumference of a circle to its diameter.

Euler's identity is also sometimes called "Euler's equation".

Derivation

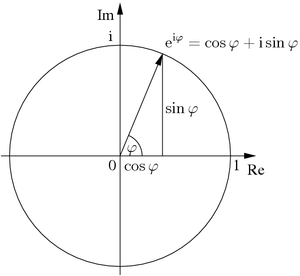
The identity is a special case of Euler's formula from complex analysis, which states that

${\displaystyle e^{ix}=\cos x+i\sin x\,\!}$

for any real number x. In particular, if ${\displaystyle x=\pi \,\!}$, then

${\displaystyle e^{i\pi }=\cos \pi +i\sin \pi \,\!}$.

Since

${\displaystyle \cos \pi =-1\,\!}$

and

${\displaystyle \sin \pi =0\,\!}$,

it follows that

${\displaystyle e^{i\pi }=-1\,\!}$

which gives the identity.

Perceptions of the identity

cut this shit yo

cut the crap

Notes

Template:Ent Maor p. 160 and Kasner and Newman p.103

References

• E. Kasner and J. Newman, Mathematics and the imagination (Bell and Sons, 1949) pp. 103–104
• Maor, Eli, e: The Story of a number (Princeton University Press, 1998), ISBN 0691058547

See also

• Exponential function

External links

• Euler-like equations (Equations that are similar to Euler's Identity)

• Complex analysis
• Exponentials
• Mathematical identities
• Mathematical theorems