This is an old revision of this page, as edited by D.Lazard (talk | contribs) at 14:56, 2 June 2012 (→Your question of User talk:D.Lazard: new section). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 14:56, 2 June 2012 by D.Lazard (talk | contribs) (→Your question of User talk:D.Lazard: new section)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)Noob Links for myself
| Help pages |
|---|
Changes
Thank you, Rschwieb, you've done a great job. You've been very kind. Serialsam (talk) 12:39, 28 April 2011 (UTC)
Proposal to merge removed. Comment added at https://en.wikipedia.org/Talk:Outline_of_algebraic_structures#Merge_proposal Yangjerng (talk) 14:03, 13 April 2012 (UTC)
Flat space gravity
| Archive |
|---|
|
I've not been working on the geometric algebra article for the time being. That does not mean I think it is in good shape; I think it still needs lots of work. I'll probably look at it again in time. I'm guessing that you may have some interest in learning about GR. If you want to exercise your (newly acquired?) geometric algebra skills, there might be something to interest you: a development of the math of relativistic gravitation in a Minkowski space background. Variations on this theme have been tried before, with some success. There are related articles around (Linearized gravity, Gravitoelectromagnetism). It might be fun to get an accurate feel of the maths behind gravity. Aside from a few presumptious leaps, the maths shows initial promise of being simple. Interested? Quondumcontr 17:47, 8 December 2011 (UTC)
OK. This again reminds me that I don't know where to begin :) I guess any start is good. I'd like to understand whatever important models of electromagnetism and gravitation that exist. Rschwieb (talk) 17:15, 9 December 2011 (UTC)
|
Found a new article talking extensively about the 3-1 and 1-3 difference. It'll be a while before I can look at it. Rschwieb (talk) 14:58, 16 December 2011 (UTC)
- This paper glosses over is the lack of manifest basis independence in some of the formulations. If something like the Dirac equation cannot be formulated in a manifestly basis-independent fashion, it bothers me. The (3,1) and (1,3) difference is significant in this context. I think that to explore this question by reading papers like this one in depth will diffuse your energy with little result; my inclination is to rather explore it from the persective of mathematical principles, e.g.: Can the Dirac equation be written in a manifestly basis-independent form? I suspect that as it stands it can be in the (3,1) algebra but not in (1,3); this approach should be very easy (I have in the past tackled it, and would be interested in following this route again). I also have an intriguing idea for restating the Dirac equation so that it combines all the families (electron, muon, tauon) into one equation, which if successful may give a different "preferred quadratic form" and a almost certainly a very interesting mathematical result. In any event, be aware that the question of the signature is a seriously non-trivial one; do not expect to be able to answer it. Would you like me to map a line of investigation? — Quondumc 07:15, 17 December 2011 (UTC)
- Honestly I think even that task sounds beyond me right now :) What I really need is a review of all fundamental operations in linear algebra, in "traditional" fashion side by side with "GA fashion". Then I would need to do the same thing for vector calculus. Maybe at /Basic GA? Ideally I would do some homework problems of this sort, to refamiliarize myself with how all this works. I can't imagine tackling something like Dirac's equation when I don't even fully grasp the form or meaning of Maxwell's equations and Einstein's equations. Rschwieb (talk) 14:05, 17 December 2011 (UTC)
- I've put together my attempt at a rigorous if simplistic start at /Basic GA to make sure we have the basics sutiably defined. Now perhaps we can work out what it is you want to review – point me in a direction and I'll see whether I can be useful. I'm not too sure how linear algebra will relate to vectors; I tend to use tensor notation as it seems to be more intuitive and can do most linear algebra and more. — Quondumc 19:44, 17 December 2011 (UTC)
- Honestly I think even that task sounds beyond me right now :) What I really need is a review of all fundamental operations in linear algebra, in "traditional" fashion side by side with "GA fashion". Then I would need to do the same thing for vector calculus. Maybe at /Basic GA? Ideally I would do some homework problems of this sort, to refamiliarize myself with how all this works. I can't imagine tackling something like Dirac's equation when I don't even fully grasp the form or meaning of Maxwell's equations and Einstein's equations. Rschwieb (talk) 14:05, 17 December 2011 (UTC)
One more thing I've been forgetting to tell you. There's a "rotation" section in the GA article, but no projection or reflection mentioned yet... Think you could insert these sections above Rotations? Rschwieb (talk) 17:12, 20 December 2011 (UTC)
- Sure, I'll put something in, and then we can panelbeat it. Have you had a chance to decide whether my "simplistic (but rigorous)" on GA basics approach is worth using? — Quondumc 21:20, 20 December 2011 (UTC)
- Sorry, I haven't had a chance to look at it yet. I've got a lot of stuff to do between now and February so it might be a while. Feel free to work on other projects in the meantime :) Rschwieb (talk) 13:17, 21 December 2011 (UTC)
Direction of Geometric algebra article
Update: I noticed the Projections section the fundamental identity is used to rewrite am as the sum of dot and wedge. Is there a fast way to explain why this identity should hold for inverses of vectors? Rschwieb (talk) 13:17, 21 December 2011 (UTC)
- Facepalm* of course their inverses are just scalar multiples :) I've never dealt with an algebra where units were so easy to find! Rschwieb (talk) 14:51, 21 December 2011 (UTC)
- Heh-heh. I had expected objections other than that, but I'm not saying which... — Quondumc 15:15, 21 December 2011 (UTC)
- Well, I'm not handy with the nuts and bolts yet. Another thing I was going to propose is that Geometric calculus can probably fill its own page. We should get a userspace draft going. That would help make the GA article more compact. Rschwieb (talk) 15:23, 21 December 2011 (UTC)
- It makes sense that a separate Geometric calculus page would be worthwhile, and that it should be linked to as the main article. What is currently in the article is very short, and probably would not be made much more compact, but should remain as a thumbnail of the main article. I think the existing disambiguation page should simply be replaced: it is not necessary. — Quondumc 16:27, 21 December 2011 (UTC)
- I know what's there now is nice, but consider that it might be better just to have a sentence or two about what GC accomplishes and a Main template to the GC article. To me this seems like the best of all worlds, contentwise. Rschwieb (talk) 16:42, 21 December 2011 (UTC)
- Now you're talking to the purist in me. This is exactly how I feel it should be: with the absolute minimum of duplication. Developing computer source code for maintainability hones this principle to a discipline. There is a strong tendency amongst some to go in the opposite direction, and an even higher principle is that we all need to find a consensus, so I usually don't push my own ideal. — Quondumc 08:31, 22 December 2011 (UTC)
- I know what's there now is nice, but consider that it might be better just to have a sentence or two about what GC accomplishes and a Main template to the GC article. To me this seems like the best of all worlds, contentwise. Rschwieb (talk) 16:42, 21 December 2011 (UTC)
- It makes sense that a separate Geometric calculus page would be worthwhile, and that it should be linked to as the main article. What is currently in the article is very short, and probably would not be made much more compact, but should remain as a thumbnail of the main article. I think the existing disambiguation page should simply be replaced: it is not necessary. — Quondumc 16:27, 21 December 2011 (UTC)
- Well, I'm not handy with the nuts and bolts yet. Another thing I was going to propose is that Geometric calculus can probably fill its own page. We should get a userspace draft going. That would help make the GA article more compact. Rschwieb (talk) 15:23, 21 December 2011 (UTC)
On one hand, I do appreciate economy (as in proofs). On the other hand, as a teacher, I also have to encourage my students to use standard notation and to "write what they mean". If I don't do that then they inevitably descend into confusion because what they have written is nonsense and they can't see their way out. At times like that, extra writing is worth the cost. Here in a WP article though, when elaboration is a click away, we have some flexibility to minimize extra text. Some people do print this material :) Rschwieb (talk) 13:08, 22 December 2011 (UTC)
- A complete sidetrack, but related: I found these interesting snippets by Lounesto, and though they might interest you: , , . — Quondum✎ 09:55, 24 January 2012 (UTC)
Defining "abelian ring"
| Extended content |
|---|
|
The article section Idempotence#Idempotent ring elements defines an abelian ring as "A ring in which all idempotents are central". Corroboration can be found, e.g. here. Since this is a variation on the other meanings associated with abelian, it seems this should be defined, either in a section in Ring (mathematics) or in its own article Abelian ring. It seems more common to define an abelian ring as a ring in which the multiplication operation is commutative, so this competing definition should be mentioned too. Your feeling? — Quondum✎ 09:14, 21 January 2012 (UTC)
Err... – what am I missing? Surely if abelian ring is not notable enough for (ii) or (iii), then it would not be notable enough for (i)? — Quondum✎ 19:19, 24 January 2012 (UTC)
|
The two idempotents being central only comes into play for the ring decomposition, and I think I can convince you where they come from. If R is the direct sum of two rings, say A and B, then obviously the identity elements of A and B are each central idempotents in R, and the ordered pair with the two identities is the identity of R! Conversely if R can be written as the direct sum of ideals A and B, then the identity of R has a unique representation as a+b=1 of elements in those rings. It's easy to see that A and B are ideals of R, and by definition of the decomposition A∩B=0. I'll leave you to prove that a and b are central idempotents and that a is the identity of A and b is the identity of B. Rschwieb (talk) 23:31, 27 January 2012 (UTC)
- Yes, it's kinda obvious when you put it like that. I think I'm getting the feel of an ideal, though this is not necessary to understand the argument, depending on what definition of "direct sum" you use. The "uniqueness" of my left- and right- decompositions seems pretty pointless. The proof you "leave to me" seems so simple that I'm worried I'm using circular arguments. When I originally saw a while back that a subring does not need the same identity element as the ring, I was taken aback. I like the decomposition into prime ideals. In particle physics, spinors (particles) seem to decompose in such a way into "left-handed" and "right-handed" "circular polarizations". — Quondum✎ 06:59, 28 January 2012 (UTC)
- Decomposition: the Krull Schmidt theorem is the most basic version of what algebraists expect to happen. I can see that the unfamiliarity with direct sum is making it harder to understand, so I'll try to sum it up. Expressing a module as a direct sum basically splits it into neat pieces. The KST says that certain modules can be split into unsplittable pieces, and another such factorization must have factors isomorphic to the first one, in some order.
- Ideals: Here is how I would try to help a students sort them out. I think we've already discussed that modules are just "vector spaces" over rings other than fields, and you are forced to distinguish between multiplication on the left and right since R doesn't have to be commutative. Just like you can think of a field as a vector space over itself, you can think of a ring as being a module over itself. However, F only has two subspaces (the trivial ones) but a ring may have more right submodules (right subspaces) than just the trivial ones. These are exactly the right ideals.
- From another point of view, I'm sure you've seen right ideals described as additive subgroups of R which "absorb" multiplication by ring elements on the right, and ideals absorb on both sides. This is a bit different from fields, which again, only have trivial ideals. Even matrix rings over fields only have trivial two-sided ideals (although they have many many onesided ideals).
- The next thing I find helpful is the analogy of normal subgroups being the kernels of group homomorphisms. Ideals of R are exactly the kernels of ring homomorphisms from R to other rings. Right ideals are precisely the kernels of module homomorphisms from R to other modules. These two types of homomorphisms are of course completely different right? A module homomorphism doesn't have to satisfy f(xy)=f(x)f(y), and a ring homomorphism doesn't have to satisfy f(xr)=f(x)r.
- Finally in connection with the last point, it's important to know that forming the quotient R/A, while it is always of course a quotient of groups, needs special conditions on A to be anything more. If A is a right ideal, then R/A is a right R module. If A is an ideal, then R/A is a ring. If A has no absorption properties, then R/A may have no special structure beyond being a group. Rschwieb (talk) 15:01, 28 January 2012 (UTC)
Tensor calculus in physics? (instead of GA)
(Moved this discussion to User talk:Rschwieb/Physics notes.)
Happy that you moved all that to somewhere more useful. =)
FYI, you might link your subpage User:Rschwieb/Physics notes to my sandbox User:F=q(E+v^B)/sandbox. It will be a summary of the most fundamental, absolutely core, essential principles of physics (right now havn't had much chance to finish it):
- the fundamental laws of Classical mechanics (CM), Statistical mechanics (SM), QM, EM, GR, and
- a summary of the dynamical variables in each formalism; CM - vectors (fields), EM - scalars/vectors (fields), GR - 4-vectors/tensors (fields), QM - operators (mostly linear), and
- some attempt made at scratching the surface of the theory at giddy heights way way up there: Relativistic QM (RQM) (from which QFT, QCD, QED, Electroweak theory, the particle physics Standard model etc. follows).
- postulates of QM and GR,
- intrinsic physical concepts: GR - reference frames and Lorentz transformations, non-Euclidean (hyperbolic) spacetime, invariance, simultaneity, QM - commutations between quantum operators and uncertainty relations, Fourier transform symmetry in wavefunctions (although mathematical identities, still important and interesting)
- symmetries and conservation
- general concepts of state, phase, configeration spaces
- some attributes of chaos theory, and how it arises in these theories
There may be errors that need clarification or correction, don't rely on it too heavily right now.
Feel free to remove this notice after linking, if so. =) Best wishes, F = q(E+v×B) ⇄ ∑ici 21:04, 1 April 2012 (UTC)
- It looks like a nice cheatsheet/study guide. Thanks for alerting me to it! I would not even know of the existence of half of these things, so it's good to have them all in one spot when I eventually come to read about them.
- The goal of my physics page is to be a source of pithy statements to motivate the material. I think physicists and engineers have more of these on hand than I do! Rschwieb (talk) 13:47, 2 April 2012 (UTC)
- That’s very nice of you to say! I promise it will be more than just a cheat sheet though (not taken as an insult! it does currently look lousy). F = q(E+v×B) ⇄ ∑ici 17:52, 2 April 2012 (UTC)
rings in matrix multiplication
Hi, you seem to be an expert in mathematical ring theory. Recently I have been re-writing matrix multiplication because the article was atrocious for its importance. Still the term "ring" is dotted all over the article anyway, maybe you could check its used correctly (instead of "field"? Although they appear to be some type of set satisfying axioms, like a group, field, or vector space, I haven’t a clue what they are in detail, and all these appear to be so similar anyway...). In particular here under "Scalar multiplication is defined:"
- "where λ is a scalar (for the second identity to hold, λ must belong to the centre of the ground ring — this condition is automatically satisfied if the ground ring is commutative, in particular, for matrices over a field)."
what does "belong to the centre of the ground ring" mean? Could you somehow re-word this and/or provide relevant links (if any) for the reader? ("Commutative" has an obvious meaning). Thank you... F = q(E+v×B) ⇄ ∑ici 14:21, 8 April 2012 (UTC)
- OK, I'll take a look at it. You can just think of rings as fields that don't have inverses for all nonzero elements, and don't have to have commutative multiplication. I think I know what the author had in mind in the section you are looking at. Rschwieb (talk) 15:06, 8 April 2012 (UTC)
- Thanks for your edits. Although there doesn't seem to be any link to "ground ring"... I can live with it. It’s just that the reader would be better served if one existed. At least you re-worded the text and linked "centre". F = q(E+v×B) ⇄ ∑ici 17:17, 8 April 2012 (UTC)
- "Ground ring" just means "ring where the coefficients come from". I couldn't think of a link for that, but maybe it should be introduced earlier in the article. Rschwieb (talk) 17:31, 8 April 2012 (UTC)
- It's not too obvious where to introduce it (a little restructuring is still needed to allow this). The idea is that the elements of the matrix and the multiplying scalars can all be elements of any chosen ring (the ground ring, though I'm not familiar with the term). F, if you are not sure of any details, I'm happy to help too if you wish; I just don't want to get in the way of any rewrite. — Quondum 19:00, 8 April 2012 (UTC)
- Thanks for your edits. Although there doesn't seem to be any link to "ground ring"... I can live with it. It’s just that the reader would be better served if one existed. At least you re-worded the text and linked "centre". F = q(E+v×B) ⇄ ∑ici 17:17, 8 April 2012 (UTC)
- I didn't realize the response, sorry (not on the watchlist... it will be added). No need to worry about the re-write, its pretty much done and you should feel free to edit anyway. =)
- IMO wouldn't it be easier to just state the matrix elements are "numbers or expressions", since most people will grip that easier than the term "elements of a ring" every now and then (even though technically necessary), and perhaps describe the properties of matrix products in terms of rings in a separate (sub)section? Well, it's better if you two decide on how to tweak any bits the reader can't easily access or understand... (not sure about you two, but the terminology is really odd: can understand the names "set, group, vector space", but "ring, ground ring, torsonal ring..."? strange names...)
- In any case, thanks to both of you for helping. =) F = q(E+v×B) ⇄ ∑ici 19:55, 9 April 2012 (UTC)
- You make a good point. There is a choice to be made: the article should either describe matrix multiplication in familiar terms and follow this with a more abstract section generalizing it to rings as the scalars, or else it should introduce the concepts of a ring, a centre, a ground ring, etc., then define the matrix multiplication in terms of this. I think that while the second approach may appeal to mathematicians familiar with the concepts of abstract algebra, the bulk of target audience for this article would not be mathematicians, making the first approach more appropriate. — Quondum 20:16, 9 April 2012 (UTC)
- Agreed with the former (separate, abstract explanations in its own section, keeping the general definition as familiar as possible). Even with just numbers (integers!), matrix multiplication is quite a lot to take in for anyone (at a first read, of course trivial with practice...). That’s without using the abstract terminology and definitions. Definitions through abstract algebra would probably switch off even scientists/engineers who know enough maths for calculations but not pure mathematical theory, never mind a lay reader... F = q(E+v×B) ⇄ ∑ici 20:26, 9 April 2012 (UTC)
Examples
Sorry for the late response and then taking extraordinarily long to produce fairly low quality examples anyway... =( I'll just keep updating this section every now and then... Please do feel free to ask about/critisise them. F = q(E+v×B) ⇄ ∑ici 16:27, 13 April 2012 (UTC)
- Thanks for anything you produce along these lines. I had never seen the agenda of physics laid out like you did on your page, and I think I'm going to learn a lot from it. All the physics classes I took were just trees in the forest but never the forest. Rschwieb (talk) 18:17, 13 April 2012 (UTC)
A barnstar for you!

|
The Editor's Barnstar |
| Congratulations, Rschwieb, you've recently made your 1,000th edit to articles on English Misplaced Pages!
Thank you so much for helping improve math-related content on Misplaced Pages. Your hard work is very much appreciated! Maryana (WMF) (talk) 19:47, 13 April 2012 (UTC) |
Possible geometric interpretation of tensors?
Hi, recently yourself, F=q(E+v^B), and Quondum, and me briefly talked about tensors and geometry. Also noticed you said here "indices obfuscate the geometry" (couldn't agree more). I have been longing to "draw a tensor" to make clear the geometric interpretation, it’s easy to draw a vector and vector field, but a tensor? Taking the first step, is this a correct possible geometric diagram of a vector transformed by a dyadic to another vector, i.e. if one arrow is a vector, then two arrows for a dyadic (for each pair of directions corresponding to each basis of those directions)? In a geometric context the number of indices corresponds to the number of directions associated with the transformation? (i.e. vectors only need one index for each basis direction, but the dyadics need two - to map the initial basis vectors to final)?
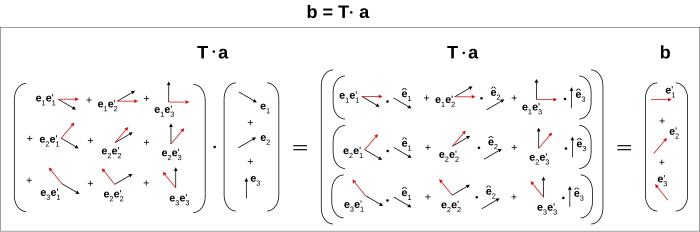
Analagously for a triadic, would three indices correspond to three directions (etc. up to n order tensors)? Thanks very much for your response, I'm busy but will check every now and then. If this is correct it may be added to the dyadic article. Feel free to criticize wherever I'm wrong. Best, Maschen (talk) 22:29, 27 April 2012 (UTC)
- First of all, I want to say that I like it and it is interesting, but I don't think it would go well in the article. I think it's a little too original for an encyclopedia. But don't let this cramp your style for pursuing the angle! Rschwieb (talk) 01:42, 28 April 2012 (UTC)
- Ok, I'll not add it to any article, the main intent is to get the interpretation right. Is this actually the right way of "drawing a dyadic", as a set of two-arrow components, or not? Also the reason for picking on dyadics is because the are several 2nd order tensors in physics, which have this geometric idea: usually in the tensor is a property of the material/object in question, and is related to the directional response of one quantity to another, such as
an applied to a material/object of results in in the material/object, given by angular velocity ω moment of inertia I an angular momentum L electric field E Electrical conductivity σ a current density flow J electric field E polarizability α (related is the permittivity ε, Electric susceptibility χE) an induced polarization field P
- (obviously there are many more examples) all of which have a similar directional relations to the above diagram (except usually both basis are the standard Cartesian type). Anyway thanks for an encouraging response. I'll also not distract you with this (inessential) favour, I just hope we can both again geometric insight to tensors, and the connection between indices and directions (btw - its not the number of dimensions that concerns me, only directions, in that tensors seem to geometrically be multidirectional quantities). Maschen (talk) 07:11, 28 April 2012 (UTC)
- Just to warn you, I think you'll find both my geometric sense and my physical sense severely disappointing
 That said, I will find it pleasant to ponder such thoughts, in an attempt to improving both of those senses. Rschwieb (talk) 21:27, 28 April 2012 (UTC)
That said, I will find it pleasant to ponder such thoughts, in an attempt to improving both of those senses. Rschwieb (talk) 21:27, 28 April 2012 (UTC)
- Just to warn you, I think you'll find both my geometric sense and my physical sense severely disappointing
- If I may comment, I suspect some geometric insight may be obtained via a geometric algebra interpretation. Keeping in mind that correspondence is only loose, a dyadic or 2nd-order tensor corresponds roughly with a bivector rather than a pair of vectors, even though an ordered pair of vectors specifies a simple dyadic. There are fewer degrees of freedom in the simple dyadic than in an ordered pair of vectors. So I'd suggest that a dyadic is better interpreted as an oriented 2D disc than two vectors, and a triadic as an oriented 3D element rather than as three vectors etc., but again this is not complete (a dyadic has more dimensions of freedom than an oriented disc has, and thus is more "general": the geometric elements described correspond rigorously to the fully antisymmetric part of a dyadic, triadic etc.). In general, a dyadic can represent a general linear mapping of a vector onto a vector, including dilation (differentially in orthogonal directions) and rotations. Geometrically this is a little difficult to draw component-wise. — Quondum 22:12, 28 April 2012 (UTC)
- Thanks Quondum, I geuss this highlights the problem with my understanding... dyadics, bivectors, 2nd order tensors, linear transformations... seem loosely similar with subtleties I'm not completely familiar with inside out. The oriented disc concept seems to be logical, but what does the oriented disk correspond to? The transformation from one vector to another? (this is such an itchy for me question because I always have to draw things before understanding them, even if its just arrows and shapes...) Maschen (talk) 13:05, 29 April 2012 (UTC)
- The oriented disc is not a good representation of a general linear transformation (too few degrees of freedom, for one) except in the limited sense of a rotation, but is a more directly geometric concept in the way a vector is. It has magnitude (area) and orientation (including direction around its edge, making it signed), but no specific shape; it is an example of something that can be depicted geometrically. Examples include an oriented parallelogram defined by two edge vectors, torque and angular momentum: pretty much anything you'd calculate conventionally using the cross product of two true vectors. If you want to go into detail it may make sense to continue on your talk page to avoid cluttering Rschwieb's. I'm watching it, so will pick up if you post a question there; you can also attract my attention more immediately on my talk page. — Quondum 16:42, 29 April 2012 (UTC)
- Ok. Thanks/apologies Quondum and Rschwieb, I don't have much more to ask for now. Quondum, feel free to remove my talk page from your watchlist (not active), I may ask on yours in the future... Maschen (talk) 05:28, 30 April 2012 (UTC)
- The oriented disc is not a good representation of a general linear transformation (too few degrees of freedom, for one) except in the limited sense of a rotation, but is a more directly geometric concept in the way a vector is. It has magnitude (area) and orientation (including direction around its edge, making it signed), but no specific shape; it is an example of something that can be depicted geometrically. Examples include an oriented parallelogram defined by two edge vectors, torque and angular momentum: pretty much anything you'd calculate conventionally using the cross product of two true vectors. If you want to go into detail it may make sense to continue on your talk page to avoid cluttering Rschwieb's. I'm watching it, so will pick up if you post a question there; you can also attract my attention more immediately on my talk page. — Quondum 16:42, 29 April 2012 (UTC)
Your question of User talk:D.Lazard
I have answered there.
Sincerely D.Lazard (talk) 14:56, 2 June 2012 (UTC)
 and
and  .
.

