This is an old revision of this page, as edited by Stephan Leeds (talk | contribs) at 05:54, 2 May 2024 (→top: nonsense “Race conditions can occur especially in logic circuits software programs.” (missing conjunction in sub- or superseries)). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 05:54, 2 May 2024 by Stephan Leeds (talk | contribs) (→top: nonsense “Race conditions can occur especially in logic circuits software programs.” (missing conjunction in sub- or superseries))(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) When a system's behavior depends on timing of uncontrollable events "Critical race" redirects here. For the academic movement, see Critical race theory.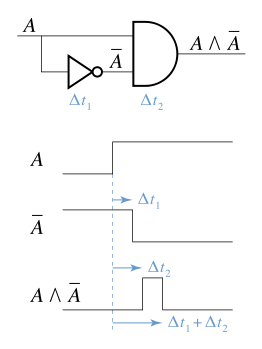
A race condition or race hazard is the condition of an electronics, software, or other system where the system's substantive behavior is dependent on the sequence or timing of other uncontrollable events, leading to unexpected or inconsistent results. It becomes a bug when one or more of the possible behaviors is undesirable.
The term race condition was already in use by 1954, for example in David A. Huffman's doctoral thesis "The synthesis of sequential switching circuits".
Race conditions can occur especially in logic circuits or multithreaded or distributed software programs.
In electronics
A typical example of a race condition may occur when a logic gate combines signals that have traveled along different paths from the same source. The inputs to the gate can change at slightly different times in response to a change in the source signal. The output may, for a brief period, change to an unwanted state before settling back to the designed state. Certain systems can tolerate such glitches but if this output functions as a clock signal for further systems that contain memory, for example, the system can rapidly depart from its designed behaviour (in effect, the temporary glitch becomes a permanent glitch).
Consider, for example, a two-input AND gate fed with the following logic: A logic signal on one input and its negation, (the ¬ is a Boolean negation), on another input in theory never output a true value: . If, however, changes in the value of take longer to propagate to the second input than the first when changes from false to true then a brief period will ensue during which both inputs are true, and so the gate's output will also be true.
A practical example of a race condition can occur when logic circuitry is used to detect certain outputs of a counter. If all the bits of the counter do not change exactly simultaneously, there will be intermediate patterns that can trigger false matches.
Critical and non-critical forms
A critical race condition occurs when the order in which internal variables are changed determines the eventual state that the state machine will end up in.
A non-critical race condition occurs when the order in which internal variables are changed does not determine the eventual state that the state machine will end up in.
Static, dynamic, and essential forms
A static race condition occurs when a signal and its complement are combined.
A dynamic race condition occurs when it results in multiple transitions when only one is intended. They are due to interaction between gates. It can be eliminated by using no more than two levels of gating.
An essential race condition occurs when an input has two transitions in less than the total feedback propagation time. Sometimes they are cured using inductive delay line elements to effectively increase the time duration of an input signal.
Workarounds
Design techniques such as Karnaugh maps encourage designers to recognize and eliminate race conditions before they cause problems. Often logic redundancy can be added to eliminate some kinds of races.
As well as these problems, some logic elements can enter metastable states, which create further problems for circuit designers.
In software
A race condition can arise in software when a computer program has multiple code paths that are executing at the same time. If the multiple code paths take a different amount of time than expected, they can finish in a different order than expected, which can cause software bugs due to unanticipated behavior. A race can also occur between two programs, resulting in security issues (see below.)
Critical race conditions cause invalid execution and software bugs. Critical race conditions often happen when the processes or threads depend on some shared state. Operations upon shared states are done in critical sections that must be mutually exclusive. Failure to obey this rule can corrupt the shared state.
A data race is a type of race condition. Data races are important parts of various formal memory models. The memory model defined in the C11 and C++11 standards specify that a C or C++ program containing a data race has undefined behavior.
A race condition can be difficult to reproduce and debug because the end result is nondeterministic and depends on the relative timing between interfering threads. Problems of this nature can therefore disappear when running in debug mode, adding extra logging, or attaching a debugger. A bug that disappears like this during debugging attempts is often referred to as a "Heisenbug". It is therefore better to avoid race conditions by careful software design.
Example
Assume that two threads each increment the value of a global integer variable by 1. Ideally, the following sequence of operations would take place:
| Thread 1 | Thread 2 | Integer value | |
|---|---|---|---|
| 0 | |||
| read value | ← | 0 | |
| increase value | 0 | ||
| write back | → | 1 | |
| read value | ← | 1 | |
| increase value | 1 | ||
| write back | → | 2 |
In the case shown above, the final value is 2, as expected. However, if the two threads run simultaneously without locking or synchronization (via semaphores), the outcome of the operation could be wrong. The alternative sequence of operations below demonstrates this scenario:
| Thread 1 | Thread 2 | Integer value | |
|---|---|---|---|
| 0 | |||
| read value | ← | 0 | |
| read value | ← | 0 | |
| increase value | 0 | ||
| increase value | 0 | ||
| write back | → | 1 | |
| write back | → | 1 |
In this case, the final value is 1 instead of the expected result of 2. This occurs because here the increment operations are not mutually exclusive. Mutually exclusive operations are those that cannot be interrupted while accessing some resource such as a memory location.
Data race
Not all regard data races as a subset of race conditions. The precise definition of data race is specific to the formal concurrency model being used, but typically it refers to a situation where a memory operation in one thread could potentially attempt to access a memory location at the same time that a memory operation in another thread is writing to that memory location, in a context where this is dangerous. This implies that a data race is different from a race condition as it is possible to have nondeterminism due to timing even in a program without data races, for example, in a program in which all memory accesses use only atomic operations.
This can be dangerous because on many platforms, if two threads write to a memory location at the same time, it may be possible for the memory location to end up holding a value that is some arbitrary and meaningless combination of the bits representing the values that each thread was attempting to write; this could result in memory corruption if the resulting value is one that neither thread attempted to write (sometimes this is called a 'torn write'). Similarly, if one thread reads from a location while another thread is writing to it, it may be possible for the read to return a value that is some arbitrary and meaningless combination of the bits representing the value that the memory location held before the write, and of the bits representing the value being written.
On many platforms, special memory operations are provided for simultaneous access; in such cases, typically simultaneous access using these special operations is safe, but simultaneous access using other memory operations is dangerous. Sometimes such special operations (which are safe for simultaneous access) are called atomic or synchronization operations, whereas the ordinary operations (which are unsafe for simultaneous access) are called data operations. This is probably why the term is data race; on many platforms, where there is a race condition involving only synchronization operations, such a race may be nondeterministic but otherwise safe; but a data race could lead to memory corruption or undefined behavior.
Example definitions of data races in particular concurrency models
The precise definition of data race differs across formal concurrency models. This matters because concurrent behavior is often non-intuitive and so formal reasoning is sometimes applied.
The C++ standard, in draft N4296 (2014-11-19), defines data race as follows in section 1.10.23 (page 14)
Two actions are potentially concurrent if
- they are performed by different threads, or
- they are unsequenced, and at least one is performed by a signal handler.
The execution of a program contains a data race if it contains two potentially concurrent conflicting actions, at least one of which is not atomic, and neither happens before the other, except for the special case for signal handlers described below . Any such data race results in undefined behavior.
The parts of this definition relating to signal handlers are idiosyncratic to C++ and are not typical of definitions of data race.
The paper Detecting Data Races on Weak Memory Systems provides a different definition:
"two memory operations conflict if they access the same location and at least one of them is a write operation... "Two memory operations, x and y, in a sequentially consistent execution form a race 〈x,y〉, iff x and y conflict, and they are not ordered by the hb1 relation of the execution. The race 〈x,y〉, is a data race iff at least one of x or y is a data operation.
Here we have two memory operations accessing the same location, one of which is a write.
The hb1 relation is defined elsewhere in the paper, and is an example of a typical "happens-before" relation; intuitively, if we can prove that we are in a situation where one memory operation X is guaranteed to be executed to completion before another memory operation Y begins, then we say that "X happens-before Y". If neither "X happens-before Y" nor "Y happens-before X", then we say that X and Y are "not ordered by the hb1 relation". So, the clause "...and they are not ordered by the hb1 relation of the execution" can be intuitively translated as "...and X and Y are potentially concurrent".
The paper considers dangerous only those situations in which at least one of the memory operations is a "data operation"; in other parts of this paper, the paper also defines a class of "synchronization operations" which are safe for potentially simultaneous use, in contrast to "data operations".
The Java Language Specification provides a different definition:
Two accesses to (reads of or writes to) the same variable are said to be conflicting if at least one of the accesses is a write...When a program contains two conflicting accesses (§17.4.1) that are not ordered by a happens-before relationship, it is said to contain a data race...a data race cannot cause incorrect behavior such as returning the wrong length for an array.
A critical difference between the C++ approach and the Java approach is that in C++, a data race is undefined behavior, whereas in Java, a data race merely affects "inter-thread actions". This means that in C++, an attempt to execute a program containing a data race could (while still adhering to the spec) crash or could exhibit insecure or bizarre behavior, whereas in Java, an attempt to execute a program containing a data race may produce undesired concurrency behavior but is otherwise (assuming that the implementation adheres to the spec) safe.
Sequential Consistency for Data Race Freedom
An important facet of data races is that in some contexts, a program that is free of data races is guaranteed to execute in a sequentially consistent manner, greatly easing reasoning about the concurrent behavior of the program. Formal memory models that provide such a guarantee are said to exhibit an "SC for DRF" (Sequential Consistency for Data Race Freedom) property. This approach has been said to have achieved recent consensus (presumably compared to approaches which guarantee sequential consistency in all cases, or approaches which do not guarantee it at all).
For example, in Java, this guarantee is directly specified:
A program is correctly synchronized if and only if all sequentially consistent executions are free of data races.
If a program is correctly synchronized, then all executions of the program will appear to be sequentially consistent (§17.4.3).
This is an extremely strong guarantee for programmers. Programmers do not need to reason about reorderings to determine that their code contains data races. Therefore they do not need to reason about reorderings when determining whether their code is correctly synchronized. Once the determination that the code is correctly synchronized is made, the programmer does not need to worry that reorderings will affect his or her code.
A program must be correctly synchronized to avoid the kinds of counterintuitive behaviors that can be observed when code is reordered. The use of correct synchronization does not ensure that the overall behavior of a program is correct. However, its use does allow a programmer to reason about the possible behaviors of a program in a simple way; the behavior of a correctly synchronized program is much less dependent on possible reorderings. Without correct synchronization, very strange, confusing and counterintuitive behaviors are possible.
By contrast, a draft C++ specification does not directly require an SC for DRF property, but merely observes that there exists a theorem providing it:
[Note:It can be shown that programs that correctly use mutexes and memory_order_seq_cst operations to prevent all data races and use no other synchronization operations behave as if the operations executed by their constituent threads were simply interleaved, with each value computation of an object being taken from the last side effect on that object in that interleaving. This is normally referred to as “sequential consistency”. However, this applies only to data-race-free programs, and data-race-free programs cannot observe most program transformations that do not change single-threaded program semantics. In fact, most single-threaded program transformations continue to be allowed, since any program that behaves differently as a result must perform an undefined operation.— end note
Note that the C++ draft specification admits the possibility of programs that are valid but use synchronization operations with a memory_order other than memory_order_seq_cst, in which case the result may be a program which is correct but for which no guarantee of sequentially consistency is provided. In other words, in C++, some correct programs are not sequentially consistent. This approach is thought to give C++ programmers the freedom to choose faster program execution at the cost of giving up ease of reasoning about their program.
There are various theorems, often provided in the form of memory models, that provide SC for DRF guarantees given various contexts. The premises of these theorems typically place constraints upon both the memory model (and therefore upon the implementation), and also upon the programmer; that is to say, typically it is the case that there are programs which do not meet the premises of the theorem and which could not be guaranteed to execute in a sequentially consistent manner.
The DRF1 memory model provides SC for DRF and allows the optimizations of the WO (weak ordering), RCsc (Release Consistency with sequentially consistent special operations), VAX memory model, and data-race-free-0 memory models. The PLpc memory model provides SC for DRF and allows the optimizations of the TSO (Total Store Order), PSO, PC (Processor Consistency), and RCpc (Release Consistency with processor consistency special operations) models. DRFrlx provides a sketch of an SC for DRF theorem in the presence of relaxed atomics.
Computer security
Many software race conditions have associated computer security implications. A race condition allows an attacker with access to a shared resource to cause other actors that utilize that resource to malfunction, resulting in effects including denial of service and privilege escalation.
A specific kind of race condition involves checking for a predicate (e.g. for authentication), then acting on the predicate, while the state can change between the time of check and the time of use. When this kind of bug exists in security-sensitive code, a security vulnerability called a time-of-check-to-time-of-use (TOCTTOU) bug is created.
Race conditions are also intentionally used to create hardware random number generators and physically unclonable functions. PUFs can be created by designing circuit topologies with identical paths to a node and relying on manufacturing variations to randomly determine which paths will complete first. By measuring each manufactured circuit's specific set of race condition outcomes, a profile can be collected for each circuit and kept secret in order to later verify a circuit's identity.
File systems
Two or more programs may collide in their attempts to modify or access a file system, which can result in data corruption or privilege escalation. File locking provides a commonly used solution. A more cumbersome remedy involves organizing the system in such a way that one unique process (running a daemon or the like) has exclusive access to the file, and all other processes that need to access the data in that file do so only via interprocess communication with that one process. This requires synchronization at the process level.
A different form of race condition exists in file systems where unrelated programs may affect each other by suddenly using up available resources such as disk space, memory space, or processor cycles. Software not carefully designed to anticipate and handle this race situation may then become unpredictable. Such a risk may be overlooked for a long time in a system that seems very reliable. But eventually enough data may accumulate or enough other software may be added to critically destabilize many parts of a system. An example of this occurred with the near loss of the Mars Rover "Spirit" not long after landing. A solution is for software to request and reserve all the resources it will need before beginning a task; if this request fails then the task is postponed, avoiding the many points where failure could have occurred. Alternatively, each of those points can be equipped with error handling, or the success of the entire task can be verified afterwards, before continuing. A more common approach is to simply verify that enough system resources are available before starting a task; however, this may not be adequate because in complex systems the actions of other running programs can be unpredictable.
Networking
In networking, consider a distributed chat network like IRC, where a user who starts a channel automatically acquires channel-operator privileges. If two users on different servers, on different ends of the same network, try to start the same-named channel at the same time, each user's respective server will grant channel-operator privileges to each user, since neither server will yet have received the other server's signal that it has allocated that channel. (This problem has been largely solved by various IRC server implementations.)
In this case of a race condition, the concept of the "shared resource" covers the state of the network (what channels exist, as well as what users started them and therefore have what privileges), which each server can freely change as long as it signals the other servers on the network about the changes so that they can update their conception of the state of the network. However, the latency across the network makes possible the kind of race condition described. In this case, heading off race conditions by imposing a form of control over access to the shared resource—say, appointing one server to control who holds what privileges—would mean turning the distributed network into a centralized one (at least for that one part of the network operation).
Race conditions can also exist when a computer program is written with non-blocking sockets, in which case the performance of the program can be dependent on the speed of the network link.
Life-critical systems
Software flaws in life-critical systems can be disastrous. Race conditions were among the flaws in the Therac-25 radiation therapy machine, which led to the death of at least three patients and injuries to several more.
Another example is the energy management system provided by GE Energy and used by Ohio-based FirstEnergy Corp (among other power facilities). A race condition existed in the alarm subsystem; when three sagging power lines were tripped simultaneously, the condition prevented alerts from being raised to the monitoring technicians, delaying their awareness of the problem. This software flaw eventually led to the North American Blackout of 2003. GE Energy later developed a software patch to correct the previously undiscovered error.
Tools
Many software tools exist to help detect race conditions in software. They can be largely categorized into two groups: static analysis tools and dynamic analysis tools.
Thread Safety Analysis is a static analysis tool for annotation-based intra-procedural static analysis, originally implemented as a branch of gcc, and now reimplemented in Clang, supporting PThreads.
Dynamic analysis tools include:
- Intel Inspector, a memory and thread checking and debugging tool to increase the reliability, security, and accuracy of C/C++ and Fortran applications; Intel Advisor, a sampling based, SIMD vectorization optimization and shared memory threading assistance tool for C, C++, C#, and Fortran software developers and architects;
- ThreadSanitizer, which uses binary (Valgrind-based) or source, LLVM-based instrumentation, and supports PThreads; and Helgrind, a Valgrind tool for detecting synchronisation errors in C, C++ and Fortran programs that use the POSIX pthreads threading primitives.
- Data Race Detector is designed to find data races in the Go Programming language.
There are several benchmarks designed to evaluate the effectiveness of data race detection tools
- DataRaceBench is a benchmark suite designed to systematically and quantitatively evaluate data race detection tools which analyze multi-threaded applications written in OpenMP.
In other areas
| This section needs expansion. You can help by adding to it. (October 2016) |
Neuroscience is demonstrating that race conditions can occur in mammal brains as well.
In UK railway signalling, a race condition would arise in the carrying out of Rule 55. According to this rule, if a train was stopped on a running line by a signal, the locomotive fireman would walk to the signal box in order to remind the signalman that the train was present. In at least one case, at Winwick in 1934, an accident occurred because the signalman accepted another train before the fireman arrived. Modern signalling practice removes the race condition by making it possible for the driver to instantaneously contact the signal box by radio.
See also
- Call collision
- Concurrency control
- Deadlock
- Hazard (logic)
- Linearizability
- Racetrack problem
- Symlink race
- Synchronization (computer science)
- Time of check to time of use
- Test-and-set
References
- Huffman, David A. "The synthesis of sequential switching circuits." (1954).
- Unger, S.H. (June 1995). "Hazards, Critical Races, and Metastability". IEEE Transactions on Computers. 44 (6): 754–768. doi:10.1109/12.391185.
- "ISO/IEC 9899:2011 - Information technology - Programming languages - C". Iso.org. Retrieved 2018-01-30.
- "ISO/IEC 14882:2011". ISO. 2 September 2011. Retrieved 3 September 2011.
- Regehr, John (2011-03-13). "Race Condition vs. Data Race". Embedded in Academia.
- "Working Draft, Standard for Programming Language C++" (PDF). 2014-11-19.
- Adve, Sarita & Hill, Mark & Miller, Barton & H. B. Netzer, Robert. (1991). Detecting Data Races on Weak Memory Systems. ACM SIGARCH Computer Architecture News. 19. 234–243. 10.1109/ISCA.1991.1021616.
- ^ "Chapter 17. Threads and Locks". docs.oracle.com.
- ^ Adve, Sarita V.; Boehm, Hans-J. (2010). "Semantics of Shared Variables & Synchronization (a.k.a. Memory Models)" (PDF).
- Adve, Sarita (December 1993). Designing Memory Consistency Models For Shared-Memory Multiprocessors (PDF) (PhD thesis). Archived (PDF) from the original on 2021-12-09. Retrieved 2021-12-09.
- Kourosh Gharachorloo and Sarita V. Adve and Anoop Gupta and John L. Hennessy and Mark D. Hill, Programming for Different Memory Consistency Models, Journal of Parallel and Distributed Computing, 1992, volume 15, pages 399–407.
- Sinclair, Matthew David (2017). "Chapter 3: Efficient Support for and Evaluation of Relaxed Atomics" (PDF). Efficient Coherence and Consistency for Specialized Memory Hierarchies (PhD). University of Illinois at Urbana–Champaign.
- "CVE-2015-8461: A race condition when handling socket errors can lead to an assertion failure in resolver.c". Internet Systems Consortium. Archived from the original on 9 June 2016. Retrieved 5 June 2017.
- ^ "Vulnerability in rmtree() and remove_tree(): CVE-2017-6512". CPAN. Retrieved 5 June 2017.
- "security: stat cache *very large* race condition if caching when follow_symlink disabled". lighttpd. Retrieved 5 June 2017.
- Colesa, Adrian; Tudoran, Radu; Banescu, Sebastian (2008). "Software Random Number Generation Based on Race Conditions". 2008 10th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing. pp. 439–444. doi:10.1109/synasc.2008.36. ISBN 978-0-7695-3523-4. S2CID 1586029.
- Leveson, Nancy; Turner, Clark S. "An Investigation of Therac-25 Accidents – I". Courses.cs.vt.edu. Archived from the original on 2017-12-15.
- Poulsen, Kevin (2004-04-07). "Tracking the blackout bug". SecurityFocus. Retrieved 2011-09-19.
- "Thread Safety Analysis – Clang 10 documentation". clang.llvm.org.
- "ThreadSanitizer – Clang 10 documentation". clang.llvm.org.
- "Helgrind: a thread error detector". Valgrind.
- "Data Race Detector". Golang.
- "Data race benchmark suite". July 25, 2019 – via GitHub.
- "How Brains Race to Cancel Errant Movements". Neuroskeptic. Discover Magazine. 2013-08-03. Archived from the original on 2013-08-06. Retrieved 2013-08-07.
- Schmidt, Robert; Leventhal, Daniel K; Mallet, Nicolas; Chen, Fujun; Berke, Joshua D (2013). "Canceling actions involves a race between basal ganglia pathways". Nature Neuroscience. 16 (8): 1118–24. doi:10.1038/nn.3456. PMC 3733500. PMID 23852117.
External links
- Karam, G.M.; Buhr, R.J.A. (August 1990). "Starvation and Critical Race Analyzers for Ada". IEEE Transactions on Software Engineering. 16 (8): 829–843. doi:10.1109/32.57622.
- Fuhrer, R.M.; Lin, B.; Nowick, S.M. (March 1995). "Algorithms for the optimal state assignment of asynchronous state machines". Advanced Research in VLSI, 1995. Proceedings., 16th Conference on. pp. 59–75. doi:10.1109/ARVLSI.1995.515611. ISBN 978-0-8186-7047-3. S2CID 4435912. as PDF Archived 2021-06-10 at the Wayback Machine
- Paper "A Novel Framework for Solving the State Assignment Problem for Event-Based Specifications" by Luciano Lavagno, Cho W. Moon, Robert K. Brayton, and Alberto Sangiovanni-Vincentelli
- Wheeler, David A. (7 October 2004). "Secure programmer: Prevent race conditions—Resource contention can be used against you". IBM developerWorks. Archived from the original (PDF) on February 1, 2009. Alt URL
- Chapter "Avoid Race Conditions Archived 2014-03-09 at the Wayback Machine" (Secure Programming for Linux and Unix HOWTO)
- Race conditions, security, and immutability in Java, with sample source code and comparison to C code, by Chiral Software
- Karpov, Andrey (6 April 2009). "Interview with Dmitriy Vyukov - the author of Relacy Race Detector (RRD)".
- Microsoft Support description
- Race Condition vs. Data Race
| Concurrent computing | |
|---|---|
| General | |
| Process calculi | |
| Classic problems | |
 A logic signal
A logic signal  on one input and its negation,
on one input and its negation,  (the ¬ is a
(the ¬ is a  . If, however, changes in the value of
. If, however, changes in the value of