This is an old revision of this page, as edited by FDR (talk | contribs) at 18:06, 13 April 2007. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 18:06, 13 April 2007 by FDR (talk | contribs)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) For the flat slab at the top of a column, see Abacus (architecture). For the finite element analysis software, see ABAQUS.An abacus (plurals abacuses or abaci) is a digital calculator, often constructed as a wooden frame with beads sliding on wires. It was in use centuries before the adoption of the written Hindu-Arabic numeral system and is still widely used by merchants and clerks in China, Japan, Africa and elsewhere.
Origins
The origins of the abacus are disputed; many cultures are known to have used similar tools. It is known to have first existed in Mesopotamia and China, and was invented sometime between 1000 BC and 500 BC. The first abacus was almost certainly based on a flat stone covered with sand or dust. Words and letters were drawn in the sand; eventually numbers were added and pebbles used to aid calculations. From this, a variety of abaci were developed; the most popular were based on the bi-quinary system, using a combination of two bases (base-2 and base-5) to represent decimal numbers.
The use of the word abacus dates from before 1387, when a Middle English work borrowed the word from Latin to describe a sandboard abacus. The Latin word came from abakos, the Greek genitive form of abax ("calculating-table"). Because abax also had the sense of "table sprinkled with sand or dust, used for drawing geometric figures", some linguists speculate that the Greek word may be derived from a Semitic root, ābāq, the Hebrew word for "dust". Though details of the transmission are obscure, it may also be derived from the Phoenician word abak, meaning "sand". The plural of abacus is abaci.
Greek abacus
A tablet found on the Greek island Salamis in 1846 dates back to 300 BC making it the oldest counting board discovered so far. It was originally thought to be a gaming board. Its construction is a slab of white marble measuring 149 cm in length, 75 cm in width and 4.5 cm thick, on which are 5 groups of markings. In the center of the tablet are a set of 5 parallel lines equally divided by a vertical line, capped with a semi-circle at the intersection of the bottom-most horizontal line and the single vertical line. Below these lines is a wide space with a horizontal crack dividing it. Below this crack is another group of eleven parallel lines, again divided into two sections by a line perpendicular to them but with the semi-circle at the top of the intersection; the third, sixth and ninth of these lines are marked with a cross where they intersect with the vertical line.
Roman abacus
Main article: Roman abacus
The Late Empire Roman abacus shown here in reconstruction contains eight long grooves containing up to five beads in each and eight shorter grooves having either one or no beads in each.
The groove marked I indicates units, X tens, and so on up to millions. The beads in the shorter grooves denote fives—five units, five tens, etc., essentially in a bi-quinary coded decimal system, obviously related to the Roman numerals. The short grooves on the right may have been used for marking Roman ounces.
Chinese abacus
Main article: Chinese abacusBefore the invention of the Chinese abacus, counting rods, other symbolic methods such as tally sticks, notches on bones, and the like, were undoubtedly used as a tool for counting and calculation.
The suanpan (simplified Chinese: 算盘; traditional Chinese: 算盤; pinyin: suànpán, lit. "Counting tray") of the Chinese is similar to the Roman abacus in principle, though has a different construction, and it was designed to do both decimal and hexadecimal arithmetics.
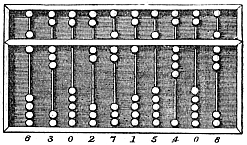
The Chinese abacus is typically around 20 cm (8 inches) tall and it comes in various widths, depending on the application and hand size of the operator. It usually has more than seven rods. There are two beads on each rod in the upper deck and five beads each in the bottom for both decimal and hexadecimal computation. The beads are usually rounded and made of a hard wood. The beads are counted by moving them up or down towards the beam. The abacus can be reset to the starting position instantly by a quick jerk along the horizontal axis to spin all the beads away from the horizontal beam at the center.
Chinese abaci can be used for functions other than counting. Unlike the simple counting board used in elementary schools, very efficient suanpan techniques have been developed to do multiplication, division, addition, subtraction, square root and cube root operations at high speed.
Bead arithmetic (Chinese: 珠算; pinyin: chùsuàn is the calculating technique used with various types of abaci, in particular the Chinese abacus. The similarity of the Roman abacus to the Chinese one suggests that one could have inspired the other, as there is some evidence of a trade relationship between the Roman Empire and China. However, no direct connection can be demonstrated, and the similarity of the abaci may be coincidental, both ultimately arising from counting with five fingers per hand. The standard Chinese abacus has 5 beads plus 2 for decimals, allows for more challenging arithmetic algorithms than the Roman model, and also allows for use with a hexadecimal numeral system.
Japanese abacus

Soroban (算盤, lit. "Counting tray") is a Japanese abacus, modified Chinese abacus (算盤). Traditional Chinese weighing units used a hexadecimal system which necessitated two beads on the upper deck. The Japanese first eliminated one bead from the upper deck and later another bead from the lower deck in each column of the Chinese abacus, making the Japanese abacus purely for the decimal system. The Japanese also eliminated the use of the Qiuchu (Chinese division table). However, the Chinese division table was still used when there were 5 lower beads. There came the debate of the multiplication table versus the division table, with the school of multiplication table prevailing in the 1920s. The rods (number of digits) usually increase to 21, 23, 27 or even 31, thus allowing calculation for more digits or representations of several different numbers at the same time. On November 12, 1946 a contest between the Japanese soroban and an electric calculator was held in Tokyo. The soroban won 4 to 1.
Soroban is taught in primary schools as a part of lessons in mathematics because the decimal numerical system can be demonstrated visually. When teaching the soroban, a song-like instruction is given by the teacher. The soroban is about 8 cm (3 inches) tall. The beads on a soroban are usually shaped as a double cone (bi-cone) to facilitate ease of movement. Often, primary school students may bring along with them two sorobans, one with 1 upper bead and 5 lower beads, the other with 1 upper bead with 4 lower beads. Despite the advent of handheld calculators, some parents send their children to private tutors to learn soroban because proficiency in soroban calculation can be easily converted to mental arithmetic at a highly advanced level.
Russian abacus

The Russian abacus, the schoty (счёты), usually has a single slanted deck, with ten beads on each wire (except one wire which has four beads, for quarter-ruble fractions). This wire is usually near the user. (Older models have another 4-bead wire for quarter-kopeks, which were minted until 1916.) The Russian abacus is often used vertically, with wires from left to right in the manner of a book. The wires are usually bowed to bulge upward in the center, in order to keep the beads pinned to either of the two sides. It is cleared when all the beads are moved to the right. During manipulation, beads are moved to the left. For easy viewing, the middle 2 beads on each wire (the 5th and 6th bead) usually have a colour different from the other 8 beads. Likewise, the left bead of the thousands wire (and the million wire, if present) may have a different color.
The Russian abacus is still in use today in shops and markets throughout the former Soviet Union, although it is no longer taught in most schools.
School abacus

Around the world, abaci have been used in pre-schools and elementary schools as an aid in teaching the numeral system and arithmetic. In Western countries, a bead frame similar to the Russian abacus but with straight wires has been common (see image). It is still often seen as a plastic or wooden toy.
The type of abacus shown here is often used to represent numbers without the use of place value. Each bead and each wire has the same value and used in this way it can represent numbers up to 100.
The most significant educational advantage of using an abacus, rather than loose beads or counters, when practicing counting and simple addition is that it gives the student an awareness of the groupings of 10 which are the foundation of our number system. Although adults take this base 10 structure for granted, it is actually difficult to learn. Many 6-year-olds can count to 100 by rote with only a slight awareness of the patterns involved.
Uses by the blind
An adapted abacus, called a Cranmer abacus is still commonly used by individuals who are blind. A piece of soft fabric or rubber is placed behind the beads so that they do not move inadvertently. This keeps the beads in place while the user feels or manipulates them. They use an abacus to perform the mathematical functions multiplication, division, addition, subtraction, square root and cubic root.
Although blind students have benefited from talking calcultors, the abacus is still very often taught to these students in early grades, both in public schools and state schools for the blind. The abacus teaches math skills that can never be replaced with talking calulators and is an important learning tool for blind students. Blind students also complete math assignments using a braille-writer and nemeth code (a type of braille code for math) but large multiplication and long division problems can be long and difficult. The abacus gives blind and visually impaired students a tool to compute math problems that equals the speed and mathmatical knowledge required by their sighted peers using pencil and paper. Many blind people find this number machine a very useful tool throughout life.
Native American abaci
| This section needs expansion. You can help by adding to it. |

Some sources mention the use of an abacus called a nepohualtzintzin in ancient Aztec culture. This Mesoamerican abacus used a 5-digit base-20 system.
The quipu of the Incas was a system of knotted cords used to record numerical data, like advanced tally sticks—but not used to perform calculations. Calculations were carried out using a yupana (quechua for "counting tool"; see figure) which was still in use after the conquest of Peru. The working principle of a yupana is unknown, but in 2001 an explanation of the mathematical basis of these instruments has been proposed: comparing the form of several yupanas, it appears that calculations were based using the Fibonacci sequence 1,1,2,3,5 and powers of 10, 20 and 40 as place values for the different fields in the instrument. Using the Fibonacci sequence would keep the number of grains within any one field at minimum.
References
- John J. O'Connor and Edmund F. Robertson. An overview of Babylonian mathematics. MacTutor History of Mathematics archive. University of St Andrews.
- Abacus. Encyclopædia Britannica.
- Video: Computers: The Abacus. Encyclopædia Britannica.
- The Invention of the Abacus. Maxfield & Montrose Interactive Inc.
- "abacus." Encyclopædia Britannica. 3 February 2007
See also
Further reading
- Pullan, J. M. (1968). The History of the Abacus. London: Books That Matter. ISBN 0-09-089410-3.
- Menninger, Karl W. (1969). Number Words and Number Symbols: A Cultural History of Numbers. MIT Press. ISBN 0-262-13040-8.
- Kojima, Takashi (1954). The Japanese Abacus: its Use and Theory. Tokyo: Charles E. Tuttle. ISBN 0-8048-0278-5.
External links
Tutorials
Abacus curiosities
- Abacus in Various Number Systems at cut-the-knot
- Java applet of Chinese, Japanese and Russian abaci
- An atomic-scale abacus
- History of the abacus and more