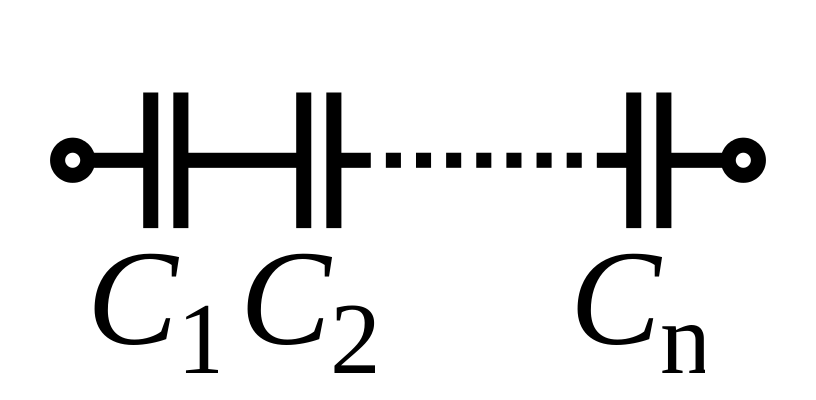Misplaced Pages

This is an old revision of this page, as edited by Light current (talk | contribs) at 15:12, 1 August 2005. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Capacitance is a measure of the amount of electric charge stored for a given electric potential. The capacitance is usually defined as the total electric charge placed on the object divided by the potential of the object:

${\displaystyle C={\frac {Q}{V}}}$

where

C is the capacitance in farads

Q is the charge in coulombs

V is the potential in volts

Detailed Definition

A capacitor is formed from any two conductors insulated from one another. The formula defining capacitance above is valid for a capacitor if it is understood that the conductors have equal but opposite charge Q, and the voltage V is the potential difference between the two conductors.

The SI unit of capacitance is the farad (F). A capacitance of one farad results in a potential of one volt for one coulomb of charge. This is a relatively large unit of capacitance. The capacitance of the majority of capacitors used in electronic circuits is several orders of magnitude smaller. The most common units of capacitance in use today are the: microfarad (μF)${\displaystyle =10^{-6}}$ F nanofarad (nF) and the picofarad (pF).

It should be noted that the above equation (C=Q/V) is only applicable for values of Q which are much larger than the electron charge e = 1.602·10 C. For example, if a capacitance of 1 pF is charged to a voltage of 100 nV, the equation would predict a charge Q = 10 C, which is smaller than the charge on a single electron.

The capacitance of a capacitor can be calculated if the geometry of the conductors and the dielectric properties of the insulator between the conductors are known. For example, the capacitance of a parallel-plate capacitor constructed of two identical plane electrodes of area A at constant spacing d is approximately equal to the following:

${\displaystyle C=\epsilon _{0}\epsilon _{r}{\frac {A}{d}}}$

where

C is the capacitance in farads

ε₀ is the permittivity of free space, measured in farad per metre

ε_r is the dielectric constant or relative permittivity of the insulator used

A is the area of each plane electrode, measured in square meters

d is the separation between the electrodes, measured in meters

Energy

The energy (measured in joules) stored in a capacitor is equal to the work done to charge it up. Consider a capacitor with capacitance C, holding a charge +q on one plate and -q on the other. Moving a small element of charge dq from one plate to the other against the potential difference V = q/C requires the work dW:

${\displaystyle dW={\frac {q}{C}}dq}$

where

W is the work measured in joules

q is the charge measured in coulombs

C is the capacitance, measured in farads

We can find the energy stored in a capacitor by integrating this equation. Starting with an uncharged capacitor (q=0) and moving charge from one plate to the other until the plates have charge +Q and -Q requires the work W:

${\displaystyle W_{charging}=\int _{0}^{Q}{\frac {q}{C}}dq={\frac {1}{2}}{\frac {Q^{2}}{C}}={\frac {1}{2}}CV^{2}=W_{stored}}$

Combining this with the above equation for the capacitance of a flat-plate capacitor, we get:

${\displaystyle W_{stored}={\frac {1}{2}}\epsilon _{0}\epsilon _{r}{\frac {A}{d}}V^{2}}$

If the maximum voltage a capacitor can withstand is ${\displaystyle V_{max}\,}$ (equal to ${\displaystyle E_{str}d\,}$ where ${\displaystyle E_{str}\,}$ is the dielectric strength), then the maximum energy it can store is:

${\displaystyle W_{max}={\frac {1}{2}}\epsilon _{0}\epsilon _{r}{\frac {A}{d}}E_{str}^{2}}$

In the design of a capacitor, the main variables are the choice of dielectric, and the "plate" dimensions. The selection of dielectric determines the relative permittivity and breakdown strength, and hence the energy capacity per unit volume of dielectric.

In electric circuits

Electrons cannot directly pass across the dielectric from one plate of the capacitor to the other. When a voltage is applied to a capacitor through an external circuit, current flows to one plate, charging it, while flowing away from the other plate, charging it oppositely. In other words, when the voltage across a capacitor changes, the capacitor will be charged or discharged. The associated current is given by

${\displaystyle I={\frac {dQ}{dt}}=C{\frac {dV}{dt}}}$

where

I is the current flowing in the conventional direction, measured in amperes

dV/dt is the time derivative of voltage, measured in volts / second.

In the case of a constant voltage (DC), an equilibrium is soon reached, where the charge of the plates corresponds with the applied voltage by the relation Q=CV, and no further current will flow in the circuit. Therefore direct current cannot pass. However, effectively alternating current (AC) can: every change of the voltage gives rise to a further charging or a discharging of the plates and therefore a current. The amount of "resistance" of a capacitor to AC is known as capacitive reactance, and varies depending on the AC frequency. Capacitive reactance is given by this formula:

${\displaystyle X_{C}={\frac {1}{2\pi fC}}}$

where

X_C = capacitive reactance, measured in ohms

f = frequency of AC in hertz

C = capacitance in farads

Thus the reactance is inversely proportional to the frequency. Since DC has a frequency of zero, the formula confirms that capacitors completely block direct current. For high-frequency alternating currents the reactance is small enough to be considered as zero in approximate analyses.

Reactance is so called because the capacitor doesn't dissipate power, but merely stores energy. In electrical circuits, as in mechanics, there are two types of load, resistive and reactive. Resistive loads (analogous to an object sliding on a rough surface) dissipate energy that enters them, ultimately by electromagnetic emission (see Black body radiation), while reactive loads (analogous to a spring or frictionless moving object) retain the energy.

The impedance of a capacitor is given by:

${\displaystyle Z={\frac {-j}{2\pi fC}}={1 \over j2\pi fC}}$

where

j is the imaginary unit = ${\displaystyle {\sqrt {-1}}}$

Hence, capacitive reactance is the negative imaginary component of impedance. The negative sign indicates that the current leads the voltage by 90° for a sinusoidal signal, as opposed to the inductor, where the current lags the voltage by 90°.

Also significant is that the impedance is inversely proportional to the capacitance, unlike resistors and inductors for which impedances are linearly proportional to resistance and inductance respectively. This is why the series and shunt impedance formulae (given below) are the inverse of the resistive case. In series, impedances sum. In shunt, conductances sum.

In a tuned circuit such as a radio receiver, the frequency selected is a function of the inductance (L) and the capacitance (C) in series, and is given by

${\displaystyle f={\frac {1}{2\pi {\sqrt {LC}}}}}$

This is the frequency at which resonance occurs in an RLC series circuit.

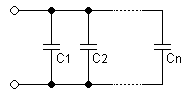
Capacitances in Series or Parallel

Capacitances in a parallel configuration each have the same potential difference (voltage). To find their total equivalent capacitance (C_eq):

${\displaystyle C_{eq}=C_{1}+C_{2}+\cdots +C_{n}\,}$

The current through capacitances in series stays the same, but the voltage across each capacitance can be different. The sum of the potential differences (voltage) is equal to the total voltage. To find their total capacitance:

${\displaystyle {\frac {1}{C_{eq}}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}}$

Capacitor/inductor duality

In mathematical terms, the ideal capacitor can be considered as an inverse of the ideal inductor, because the voltage-current equations of the two devices can be transformed into one another by exchanging the voltage and current terms.

Just as two or more inductors can be magnetically coupled to make a transformer, two or more charged conductors can be electrostatically coupled to make a capacitor. The mutual capacitance of two conductors is defined as the current that flows in one when the voltage across the other changes by unit voltage in unit time.

References

Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 2: Electricity and Magnetism, Light (4th ed.). W. H. Freeman. ISBN 1572594926

Serway, Raymond; Jewett, John (2003). Physics for Scientists and Engineers (6 ed.). Brooks Cole. ISBN 0534408427

See also

• Capacitor
• Electromagnetism
• Electricity
• Electronics
• Inductor

• Physical quantity
• Electricity