Misplaced Pages

This is an old revision of this page, as edited by FDT (talk | contribs) at 12:07, 25 April 2009 (simplifying the introduction. Sources for the modern viewpoint are in abundance, hence no need for the citations). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Part of a series on
Classical mechanics
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$Second law of motion
History Timeline Textbooks
Branches Applied Celestial Continuum Dynamics Field theory Kinematics Kinetics Statics Statistical mechanics
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Koopman–von Neumann mechanics
Core topics Damping Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational frequency Angular acceleration / displacement / frequency / velocity
Scientists Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Poisson Hamilton Jacobi Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

In classical mechanics, centrifugal force is the outward force that is associated with rotation. In recent years, the tendency has been to treat centrifugal force as a fictitious force which arises when observations are taken from a rotating frame of reference.

Derivation

Newton's law of motion for a particle of mass m can be written in vector form as

${\displaystyle {\boldsymbol {F}}=m{\boldsymbol {a}}\ ,}$

where F is the vector sum of the physical forces applied to the particle and a is the absolute acceleration of the particle, given by

${\displaystyle {\boldsymbol {a}}={\frac {d^{2}}{dt^{2}}}{\boldsymbol {r}}\ ,}$

where r is the position vector of the particle. The differentiations are performed in terms of an inertial reference frame. As shown in Rotating reference frame, for any vector Q depending upon time, its time derivative evaluated in terms of a reference frame with a coincident origin but rotating with the absolute angular velocity Ω is related to the absolute derivative dQ/dt by:

${\displaystyle {\frac {d}{dt}}{\boldsymbol {Q}}=\left+{\boldsymbol {\Omega }}\times {\boldsymbol {Q}}\ ,}$

where × denotes the vector cross product and square brackets denote evaluation in the rotating frame of reference. As a particular example, it follows that the absolute acceleration of the particle can be written as (for more detail, see Rotating frame of reference):

${\displaystyle {\begin{aligned}{\boldsymbol {a}}&={\frac {d^{2}}{dt^{2}}}{\boldsymbol {r}}\\&=\left+{\frac {d{\boldsymbol {\Omega }}}{dt}}\times {\boldsymbol {r}}+2{\boldsymbol {\Omega }}\times \left+{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}}).\end{aligned}}}$

It is sometimes convenient to treat the first term on the right hand side as if it actually were the absolute acceleration, and not merely the acceleration in the rotating frame. That is, we pretend the rotating frame is an inertial frame, and move the other terms over to the force side of the equation, and treat them as fictitious forces. When this is done, the equation of motion has the form:

${\displaystyle {\boldsymbol {F}}-m{\frac {d{\boldsymbol {\Omega }}}{dt}}\times {\boldsymbol {r}}-2m{\boldsymbol {\Omega }}\times \left-m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times {\boldsymbol {r}})}$ ${\displaystyle =m\left.}$

The last term on the left hand side (the force side) is commonly called the centrifugal force. It points directly away from the axis of rotation of the rotating reference frame, with magnitude m ${\displaystyle {\Omega }^{2}r}$.

Notice that for a non-rotating frame the centrifugal force is zero. The disappearance of centrifugal force in an inertial frame of reference is shared by all fictitious forces.

Advantages of rotating frames

A rotating reference frame can have advantages over an inertial reference frame. Sometimes the calculations are simpler (an example is inertial circles), and sometimes the intuitive picture coincides more closely with the rotational frame (an example is sedimentation in a centrifuge). By treating the extra acceleration terms due to the rotation of the frame as if they were forces, subtracting them from the physical forces, it's possible to treat the second time derivative of position (relative to the rotating frame) as if it was the absolute acceleration. Thus the analysis using Newton's law can proceed as if the reference frame was inertial, provided the fictitious force terms are included in the sum of forces. For example, centrifugal force is used in the FAA pilot's manual in describing turns. Other examples are such systems as planets, centrifuges, carousels, turning cars, spinning buckets, and rotating space stations. Regarding the advantages of rotating frames from the viewpoint of meteorology, Ryder says:

A simple way of dealing with this problem is, of course, to transform all coordinates to an inertial system. This is, however, sometimes inconvenient. Suppose, for example, we wish to calculate the movement of air masses in the earth's atmosphere due to pressure gradients. We need the results relative to the rotating frame, the earth, so it is better to stay within this coordinate system if possible. This can be achieved by introducing fictitious (or "non-existent") forces which enable us to apply Newton's Laws of Motion in the same way as in an inertial frame.

— Peter Ryder: Classical Mechanics, pp. 78-79

Centrifugal force and absolute rotation

Can absolute rotation be detected? In other words, can one decide whether an observed object is rotating or if it is you, the observer that is rotating?

Newton suggested two experiments that could resolve this problem. One is the effect of centrifugal force upon the shape of the surface of water rotating in a bucket. Newton suggested the shape of the surface of the water indicates the presence or absence of absolute rotation relative to the fixed stars: a concave surface indicates rotation of the water (see Bucket argument). Newton also proposed another experiment for this purpose using the tension in a cord joining two spheres rotating about their center of gravity: non-zero tension in the string indicates rotation of the spheres (see Rotating spheres).

The concavity of the surface of rotating water in a bucket can be explained in a simple, approximate fashion using the concept of potential energy, described next. Alternative approaches are found in Bucket argument.

In a reference frame uniformly rotating at angular rate Ω, the fictitious centrifugal force is conservative and has a potential energy of the form:

${\displaystyle {U}_{\mathrm {Cfgl} }=-{\frac {1}{2}}m\Omega ^{2}r^{2}\ ,}$

where r is the radius from the axis of rotation. This result can be verified by taking the gradient of the potential to obtain the radially outward force:

${\displaystyle F_{\mathrm {Cfgl} }=-{\frac {\partial }{\partial r}}{U}_{\mathrm {Cfgl} }}$ ${\displaystyle =m\Omega ^{2}r\ .}$

The meaning of the potential energy is that movement of a test body from a larger radius to a smaller radius involves doing work against the centrifugal force.

The potential energy is useful, for example, in understanding the concavity of the water surface in a rotating bucket. Notice that at equilibrium the surface adopts a shape such that an element of volume at any location on its surface has the same potential energy as at any other. That being so, no element of water on the surface has any incentive to move position, because all positions are equivalent in energy. That is, equilibrium is attained. On the other hand, were surface regions with lower energy available, the water occupying surface locations of higher potential energy would move to occupy these positions of lower energy, inasmuch as there is no barrier to lateral movement in an ideal liquid.

We might imagine deliberately upsetting this equilibrium situation by somehow momentarily altering the surface shape of the water to make it different from an equal-energy surface. This change in shape would not be stable, and the water would not stay in our artificially contrived shape, but engage in a transient exploration of many shapes until non-ideal frictional forces introduced by sloshing, either against the sides of the bucket or by the non-ideal nature of the liquid, killed the oscillations and the water settled down to the equilibrium shape.

To see the principle of an equal-energy surface at work, imagine gradually increasing the rate of rotation of the bucket from zero. The water surface is flat at first, and clearly a surface of equal potential energy because all points on the surface are at the same height in the gravitational field acting upon the water. At some small angular rate of rotation, however, an element of surface water can achieve lower potential energy by moving outward under the influence of the centrifugal force. Because water is incompressible and must remain within the confines of the bucket, this outward movement increases the depth of water at the larger radius, increasing the height of the surface at larger radius, and lowering it at smaller radius. The surface of the water becomes slightly concave, with the consequence that the potential energy of the water at the greater radius is increased by the work done against gravity to achieve the greater height. As the height of water increases, movement toward the periphery becomes no longer advantageous, because the reduction in potential energy from working with the centrifugal force is balanced against the increase in energy working against gravity. Thus, at a given angular rate of rotation, a concave surface represents the stable situation, and the more rapid the rotation, the more concave this surface. If rotation is arrested, the energy stored in fashioning the concave surface must be dissipated, for example through friction, before an equilibrium flat surface is restored.

To implement a surface of constant potential energy quantitatively, let the height of the water be ${\displaystyle h(r)\,}$: then the potential energy per unit mass contributed by gravity is ${\displaystyle gh(r)\ }$ and the total potential energy per unit mass on the surface is

${\displaystyle {U}={U}_{0}+gh(r)-{\frac {1}{2}}\Omega ^{2}r^{2}\,}$

with ${\displaystyle {U}_{0}}$ the background energy level independent of r. (Note: this formula for the potential energy of the water assumes the water co-rotates with the frame of reference. If, as actually is the case, the water does not quite rotate at the same rate as the frame, its energy will be somewhat different.) In a static situation (no motion of the fluid in the rotating frame), this energy is constant independent of position r. Requiring the energy to be constant, we obtain the parabolic form:

${\displaystyle h(r)={\frac {\Omega ^{2}}{2g}}r^{2}+h(0)\ ,}$

where h(0) is the height at r = 0 (the axis). See Figure 1.

The principle of operation of the centrifuge also can be simply understood in terms of this expression for the potential energy, which shows that it is favorable energetically when the volume far from the axis of rotation is occupied by the heavier substance.

Notice that this analysis based upon centrifugal potential energy requires the presence of a centrifugal force. This force is needed in a co-rotating frame of reference (one that rotates with the water) because the water appears stationary in this frame. Thus, observers looking at the stationary water need the centrifugal force to explain why the water surface is concave and not flat. In short, rotating water has a concave surface: if the surface you see is concave, and the water does not seem to you to be rotating, then you are rotating with the water. Equivalently, if you need a centrifugal force to explain what you see, then you are rotating.

Examples

Below several examples illustrate both the inertial and rotating frames of reference, and the role of centrifugal force and its relation to Coriolis force in rotating frameworks. For more examples see Fictitious force, rotating bucket and rotating spheres.

Using fictitious forces

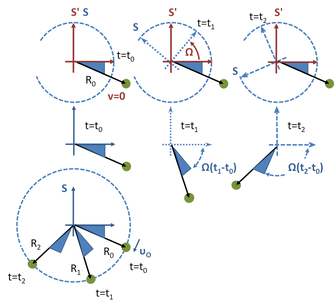
It has been mentioned that to deal with motion in a rotating frame of reference, one alternative to a solution based upon translating everything into an inertial frame instead is to apply Newton's laws of motion in the rotating frame by adding pseudo-forces, and then working directly in the rotating frame. Next is a simple example of this method.

Figure 2 illustrates that a body that is stationary relative to the non-rotating inertial frame S' appears to be rotating when viewed from the rotating frame S, which is rotating at angular rate Ω. Therefore, application of Newton's laws to what looks like circular motion in the rotating frame S at a radius R, requires an inward centripetal force of −m Ω R to account for the apparent circular motion. According to observers in S, this centripetal force in the rotating frame is provided as a net force that is the sum of the radially outward centrifugal pseudo force m Ω R and the Coriolis force −2m Ω × v_rot. To evaluate the Coriolis force, we need the velocity as seen in the rotating frame, v_rot. According to the formulas in the Derivation section, this velocity is given by −Ω × R. Hence, the Coriolis force (in this example) is inward, in the opposite direction to the centrifugal force, and has the value −2m Ω R. The combination of the centrifugal and Coriolis force is then m Ω R−2m Ω R = −m Ω R, exactly the centripetal force required by Newton's laws for circular motion.

For further examples and discussion, see below, and see Taylor.

Whirling table

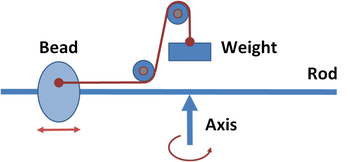
Figure 3 shows a simplified version of an apparatus for studying centrifugal force called the "whirling table". The apparatus consists of a rod that can be whirled about an axis, causing a bead to slide on the rod under the influence of centrifugal force. A cord ties a weight to the sliding bead. By observing how the equilibrium balancing distance varies with the weight and the speed of rotation, the centrifugal force can be measured as a function of the rate of rotation and the distance of the bead from the center of rotation.

From the viewpoint of an inertial frame of reference, equilibrium results when the bead is positioned to select the particular circular orbit for which the weight provides the correct centripetal force.

Dropping ball

Figure 4 shows a ball dropping vertically (parallel to the axis of rotation Ω of the rotating frame). For simplicity, suppose it moves downward at a fixed speed in the inertial frame, occupying successively the vertically aligned positions numbered one, two, three. In the rotating frame it appears to spiral downward, and the right side of Figure 4 shows a top view of the circular trajectory of the ball in the rotating frame. Because it drops vertically at a constant speed, from this top view in the rotating frame the ball appears to move at a constant speed around its circular track. A description of the motion in the two frames is next.

Inertial frame

In the inertial frame the ball drops vertically at constant speed. It does not change direction, so the inertial observer says the acceleration is zero and there is no force acting upon the ball.

Uniformly rotating frame

In the rotating frame the ball drops vertically at a constant speed, so there is no vertical component of force upon the ball. However, in the horizontal plane perpendicular to the axis of rotation, the ball executes uniform circular motion as seen in the right panel of Figure 4. Applying Newton's law of motion, the rotating observer concludes that the ball must be subject to an inward force in order to follow a circular path. Therefore, the rotating observer believes the ball is subject to a force pointing radially inward toward the axis of rotation. According to the analysis of uniform circular motion

${\displaystyle \mathbf {F} _{\mathrm {fict} }=-m\Omega ^{2}R{\boldsymbol {\hat {r}}}\ ,}$

with ${\displaystyle {\boldsymbol {\hat {r}}}}$ a unit vector in the outward radial direction, and where Ω is the angular rate of rotation, m is the mass of the ball, and R is the radius of the spiral in the horizontal plane. Because there is no apparent source for such a force (hence the label "fictitious"), the rotating observer concludes it is just "a fact of life" in the rotating world that there exists an inward force with this behavior. Inasmuch as the rotating observer already knows there is a ubiquitous outward centrifugal force in the rotating world, how can there be an inward force? The answer is the Coriolis force: the component of velocity tangential to the circular motion seen in the right panel of Figure 4 activates the Coriolis force, which cancels the centrifugal force and goes a step further to provide precisely the centripetal force demanded by the calculations of the rotating observer.

Some details of evaluation of the Coriolis force are shown in Figure 5. The Coriolis force is found to be (using the cross-product expansion):

${\displaystyle \mathbf {F_{Cor}} {\overset {\underset {\mathrm {def} }{}}{=}}-2m\mathbf {\Omega \times v} =-2m\mathbf {\Omega \times } \left(-\mathbf {\Omega \times } R{\boldsymbol {\hat {r}}}\right)=-2m\Omega ^{2}R{\boldsymbol {\hat {r}}}\ ,}$

Combining this force with the centrifugal force:

${\displaystyle \mathbf {F} _{\mathrm {fict} }=\mathbf {F_{Cor}} +\mathbf {F_{Cfgl}} =\left(-2m\Omega ^{2}R+m\Omega ^{2}R\right){\boldsymbol {\hat {r}}}=-m\Omega ^{2}R{\boldsymbol {\hat {r}}}\ ,}$

as required for the necessary centripetal force to maintain circular motion.

Because the Coriolis force and centrifugal forces combine to provide the centripetal force the rotating observer requires for the observed circular motion, the rotating observer does not need to apply any additional force to the object, in complete agreement with the inertial observer, who also says there is no force needed. One way to express the result: the fictitious forces look after the "fictitious" situation, so the ball needs no help to travel the perceived trajectory: all observers agree that nothing needs to be done to make the ball follow its path.

Parachutist

To show a different frame of reference, let's revisit the dropping ball example in Figure 4 from the viewpoint of a parachutist falling at constant speed to Earth (the rotating platform). The parachutist aims to land upon the point on the rotating ground directly below the drop-off point. Figure 6 shows the vertical path of descent seen in the rotating frame. The parachutist drops at constant speed, occupying successively the vertically aligned positions one, two, three.

In the stationary frame, let us suppose the parachutist jumps from a helicopter hovering over the destination site on the rotating ground below, and therefore traveling at the same speed as the target below. The parachutist starts with the necessary speed tangential to his path (ωR) to track the destination site. If the parachutist is to land on target, the parachute must spiral downward on the path shown in Figure 6. The stationary observer sees a uniform circular motion of the parachutist when the motion is projected downward, as in the left panel of Figure 6. That is, in the horizontal plane, the stationary observer sees a centripetal force at work, -m ω R, as is necessary to achieve the circular path. The parachutist needs a thruster to provide this force. Without thrust, the parachutist follows the dashed vertical path in the left panel of Figure 6, obeying Newton's law of inertia.

The stationary observer and the observer on the rotating ground agree that there is no vertical force involved: the parachutist travels vertically at constant speed. However, the observer on the ground sees the parachutist simply drop vertically from the helicopter to the ground, following the vertically aligned positions one, two, three. There is no force necessary. So how come the parachutist needs a thruster?

The ground observer has this view: there is always a centrifugal force in the rotating world. Without a thruster, the parachutist would be carried away by this centrifugal force and land far off the mark. From the parachutist's viewpoint, trying to keep the target directly below, the same appears true: a steady thrust radially inward is necessary, just to hold a position directly above target. Unlike the dropping ball case, where the fictitious forces conspired to produce no need for external agency, in this case they require intervention to achieve the trajectory. The basic rule is: if the inertial observer says a situation demands action or does not, the fictitious forces of the rotational frame will lead the rotational observer to the same conclusions, albeit by a different sequence.

Notice that there is no Coriolis force in this discussion, because the parachutist has zero horizontal velocity from the viewpoint of the rotating ground observer.

Skywriter

What is the viewpoint of an airplane pilot engaged in skywriting? The plane's path is the smoky trail left behind, and progress can be registered as the distance s from the start of the trail to the plane's present position. The speed of the plane is v = ds / dt and the curvature of the path is measured by the osculating circle of radius ρ that is tangent to the path. For the inertial observer watching from the ground, the plane at any instant is executing circular motion about its (instantaneous) center of curvature, and so is subject to a centripetal force v / ρ acting radially inward toward this center of curvature. To maintain trajectory, this centripetal force is provided by banking the airplane, generating a lift that provides this centripetal force. According to the pilot, however, the plane is stationary, but subject to a centrifugal force outward from the instantaneous center of curvature with a magnitude v / ρ. To maintain trajectory, this centrifugal force is combated by banking the airplane, generating a lift to counteract the centrifugal force, thereby maintaining the plane in its equilibrium motionless position. For a detailed analysis, see Mechanics of planar particle motion.

Planetary motion

Another example of great historical importance is that of planetary motion. Although planetary motion involves many planets in practice, a simple case is the two-body problem of two masses alone, mutually attracted by each others gravitation. Below is a sketch of the analysis of this case that shows how the three-dimensional problem is reduced first to motion of a single particle in a plane, and then second to a simplified one-dimensional problem based upon centrifugal force. More detail is found in the articles linked above.

Two-particle formulation in three-dimensional space

The gravitational field is the gradient of a potential V(r) given by Poisson's equation:

${\displaystyle \nabla ^{2}V=-Gm\ \delta ({\boldsymbol {r}}),}$

where ∇ is the Laplacian, δ( r ) is the Dirac delta function and mδ( r ) represents a point mass m at location r = 0. For an unbounded region, the solution is:

${\displaystyle V=V(r)=-G{\frac {m}{r}}\ ,}$

where G is the gravitational constant and r is the radial distance from the mass m originating the field. For the interesting case of two masses of masses m₁, m₂ the radial distance becomes the separation of the two masses, that is,

${\displaystyle r=|{\boldsymbol {r_{1}-r_{2}}}|\ ,}$

and the gravitational potential at the location of mass m₂ due to mass m₁ becomes

${\displaystyle V({\boldsymbol {r_{2}}})=-Gm_{1}{\frac {1}{|{\boldsymbol {r_{2}-r_{1}}}|}}\ ,}$

and the acceleration of mass m₂ becomes (from Newton's second law):

${\displaystyle m_{2}{\ddot {\boldsymbol {r_{2}}}}=Gm_{2}m_{1}{\frac {1}{|{\boldsymbol {r_{2}-r_{1}}}|^{2}}}{\hat {\boldsymbol {u}}}_{21}\ ,}$

where ${\displaystyle {\hat {\boldsymbol {u}}}_{21}}$ is a unit vector pointing from mass m₂ toward mass m₁ and double overdots represent the second time derivative. Similarly,

${\displaystyle m_{1}{\ddot {\boldsymbol {r_{1}}}}=Gm_{2}m_{1}{\frac {1}{|{\boldsymbol {r_{1}-r_{2}}}|^{2}}}{\hat {\boldsymbol {u}}}_{12}\ ,}$

where ${\displaystyle {\hat {\boldsymbol {u}}}_{12}=-{\hat {\boldsymbol {u}}}_{21}}$. Subtracting the two equations:

${\displaystyle {\frac {d^{2}}{dt^{2}}}{\boldsymbol {\left(r_{1}-r_{2}\right)}}=Gm_{1}m_{2}\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right){\frac {1}{|{\boldsymbol {r_{1}-r_{2}}}|^{2}}}{\hat {\boldsymbol {u}}}_{12}\ ,}$

or, rearranging:

${\displaystyle \mu {\frac {d^{2}}{dt^{2}}}{\boldsymbol {\left(r_{1}-r_{2}\right)}}=Gm_{1}m_{2}{\frac {1}{|{\boldsymbol {r_{1}-r_{2}}}|^{2}}}{\hat {\boldsymbol {u}}}_{12}\ ,}$

where μ is the so-called reduced mass defined by:

${\displaystyle \mu =\left({\frac {m_{1}m_{2}}{m_{1}+m_{2}}}\right)\ \ .}$

Single-particle formulation in a plane

In this way, the problem simplifies to that of a single particle of mass μ moving in the radial potential V (r) with

${\displaystyle r=|{\boldsymbol {r_{1}-r_{2}}}|\ ,}$

and

${\displaystyle V(r)=Gm_{1}m_{2}{\frac {1}{|{\boldsymbol {r_{1}-r_{2}}}|}}=Gm_{1}m_{2}{\frac {1}{r}}=\mu G\left(m_{1}+m_{2}\right)\ {\frac {1}{r}}\ ,}$

The force acting upon this particle of mass μ is therefore a radially inward force of the form, (${\displaystyle {\boldsymbol {\nabla }}}$ is the gradient operator):

${\displaystyle {\boldsymbol {F}}=-\mu {\boldsymbol {\nabla }}V(r)=k\mu {\boldsymbol {\nabla }}{\frac {1}{r}}=-k\mu {\frac {1}{r^{2}}}{\hat {\boldsymbol {r}}}\ ,}$

where ${\displaystyle k=G\left(m_{1}+m_{2}\right)\ \,}$. The unit vector ${\displaystyle {\hat {\boldsymbol {r}}}}$ points in the outward radial direction.

The trajectory of the particle is found using Newton's second law of motion. That is we solve the equation:

${\displaystyle {\frac {d^{2}}{dt^{2}}}{\boldsymbol {r}}=-k{\frac {1}{r^{2}}}{\hat {\boldsymbol {r}}}\ .}$

The solution is found most simply using polar coordinates. In polar coordinates the acceleration is given by:

${\displaystyle {\frac {d^{2}}{dt^{2}}}{\boldsymbol {r}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+{\frac {1}{r}}\quad {\dot {\overbrace {r^{2}{\dot {\theta }}} }}\quad {\hat {\boldsymbol {\theta }}}\ ,}$

where overdots indicate time derivatives, and ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ is an azimuthal unit vector perpendicular to the radial direction. Evidently, the motion is planar (in the plane of ${\displaystyle {\hat {\mathbf {r} }},\ {\hat {\boldsymbol {\theta }}}}$) because no force component is normal to this plane. Putting this acceleration into Newton's law, separate equations are found for the radial and azimuthal directions. In the azimuthal direction:

${\displaystyle {\dot {\overbrace {r^{2}{\dot {\theta }}} }}=0\ ,}$

and in the radial direction:

${\displaystyle {\ddot {r}}-r{\dot {\theta }}^{2}=-k{\frac {1}{r^{2}}}\ .}$

In this formulation, the second term on the left side is simply one of two terms in the acceleration in polar coordinates. It is not an impressed force; it is part of the mathematics of derivatives in polar coordinates.

The azimuthal equation expresses the conservation of angular momentum, where the angular momentum of the particle is its speed:

${\displaystyle v=r{\dot {\theta }}}$

multiplied by its radial position. Using this conservation equation,

${\displaystyle \mu r^{2}{\dot {\theta }}=\mu vr=\ell \ ,}$

where ${\displaystyle \ell }$ is the conserved (time independent) angular momentum. Substituting this result for ${\displaystyle {\dot {\theta }}}$ into the radial equation:

${\displaystyle {\ddot {r}}-r\left({\frac {\ell }{\mu r^{2}}}\right)^{2}=-k{\frac {1}{r^{2}}}\ ,}$

or:

${\displaystyle {\ddot {r}}-\left({\frac {v^{2}}{r}}\right)=-k{\frac {1}{r^{2}}}\ .}$

Equivalent one-dimensional formulation

By invoking the conservation of angular momentum above, the azimuthal equation need not be explicitly considered any longer. The radial equation, derived here using polar coordinates in an inertial frame of reference, can be rearranged as:

${\displaystyle {\ddot {r}}=\left({\frac {v^{2}}{r}}\right)-k{\frac {1}{r^{2}}}\ .}$

This rearranged equation can be derived from the standpoint of a co-rotating frame, or can be interpreted as a fictitious one-dimensional problem. This fictitious problem treats r as a fictional one-dimensional position coordinate (such as ordinarily would be denoted simply as x). This one-dimensional viewpoint allows us to interpret ${\displaystyle {\ddot {r}}}$ as an "acceleration". Then the one-dimensional force law is interpreted as motion of this particle subject to the two forces on the right-hand side, which are sometimes referred to as the outward centrifugal force per unit mass v/r and the inward force of gravity per unit mass -k ⁄ r. If these two forces balance :

${\displaystyle r={\frac {k}{v^{2}}}\ ,}$

and

${\displaystyle {\ddot {r}}=0}$   or   ${\displaystyle r=r(t=0)+{\dot {r}}(t=0)t\ .}$

In words, if at time t = 0 , ${\displaystyle {\dot {r}}(t=0)=0}$, r remains at the value it holds at t = 0 (namely r(t=0) = k ⁄ v) for all times t.

In the one-dimensional problem, in this case of ${\displaystyle {\dot {r}}(t=0)=0}$ and balanced forces, the particle just sits there at r = r(t=0).

As an aside, the solution above based upon a balance of the two terms is not mandated: two-body motion can lead to time-varying separation of the two bodies; see Kepler solution. In this more general case that transcends simple circular motion, the interpretation of v/r as a "centrifugal force" is less obvious, because the true centrifugal force is v/ρ, with ρ the instantaneous radius of curvature of the path in the two-dimensional interpretation, and v the velocity component tangential to the actual orbit. At a minimum, then, to justify the designation "centrifugal force" requires some additional argument. It is probably fair to say that the usage of "centrifugal force" in this connection is more an attempt at colorful language than careful usage.

Retracing the steps

Having found the solution in the one-dimensional formulation, how is it interpreted if the solution is now returned to the original problem of two particles in three-space? In one dimension the "particle" sits at a fixed point r(t=0). The relation r = k ⁄ v is difficult to interpret entirely within the one-dimensional model because the particle is stationary, so it is unclear how to interpret the "velocity" v. Thus v is simply some parameter determining the centrifugal force.

Going back to the particle in a plane (moving away from the one-dimensional problem), this particle in planar motion moves in a circle at radius r(t=0) with constant angular rate of rotation given by its angular momentum ${\displaystyle \ell }$. The relation r = k ⁄ v makes sense from an inertial standpoint, because the faster the particle moves, the smaller the radius must be to provide sufficient centripetal force via gravitational attraction to hold the particle in orbit. If, instead of an inertial frame, a co-rotating frame is chosen that rotates with the particle, the particle appears stationary but subject to a centrifugal force that balances gravity. As with the one-dimensional formulation, the centrifugal force depends on the parameter v, which is simply an unexplained parameter that determines the centrifugal force, a "fact of life" in the co-rotating frame. There is no apparent source for this force, no originating body; nonetheless this force must be invoked because it must be included in Newton's laws to deduce the correct behavior of the particle.

Going back further, to the original problem with two masses, the two rotate about their barycenter with a system angular momentum ${\displaystyle \ell }$. See Figure 8. Again the relation r = k ⁄ v makes sense from an inertial standpoint: the faster the bodies move, the closer they must be to each other to establish sufficient gravity to hold them together. Alternatively, a co-rotating frame can be chosen, with origin at the barycenter, in which the two bodies do not appear to move. Again, a fictitious centrifugal force is invoked that depends on the parameter v, which is simply a "fact of life" in the co-rotating world. (For comparison, see Rotating spheres where, instead of gravity, the tension in a cord ties the two bodies together.)

Development of the modern conception of centrifugal force

This article needs attention from an expert in History of Science. Please add a reason or a talk parameter to this template to explain the issue with the article. WikiProject History of Science may be able to help recruit an expert. (August 2008)

Early scientific ideas about centrifugal force were based upon intuitive perception, and circular motion was considered somehow more "natural" than straight line motion. According to Domenico Meli:

"For Huygens and Newton centrifugal force was the result of a curvilinear motion of a body; hence it was located in nature, in the object of investigation. According to a more recent formulation of classical mechanics, centrifugal force depends on the choice of how phenomena can be conveniently represented. Hence it is not located in nature, but is the result of a choice by the observer. In the first case a mathematical formulation mirrors centrifugal force; in the second it creates it."

There is evidence that Sir Isaac Newton originally conceived circular motion as being caused by a balance between an inward centripetal force and an outward centrifugal force.

The modern conception of centrifugal force appears to have its origins in Christiaan Huygens' paper De Vi Centrifuga, written in 1659. It has been suggested that the idea of circular motion as caused by a single force was introduced to Newton by Robert Hooke.

Newton described the role of centrifugal force upon the height of the oceans near the equator in the Principia:

COR. Since the centrifugal force of the parts of the earth, arising from the earth's diurnal motion, which is to the force of gravity as 1 to 289, raises the waters under the equator to a height exceeding that under the poles by 85472 Paris feet, as above, in Prop. XIX., the force of the sun, which we have now shewed to be to the force of gravity as 1 to 12868200, and therefore is to that centrifugal force as 289 to 12868200, or as 1 to 44527, will be able to raise the waters in the places directly under and directly opposed to the sun to a height exceeding that in the places which are 90 degrees removed from the sun only by one Paris foot and 113 V inches ; for this measure is to the measure of 85472 feet as 1 to 44527.

— Newton: Principia Corollary to Book II, Proposition XXXVI. Problem XVII

The effect of centrifugal force in countering gravity, as in this behavior of the tides, has led centrifugal force sometimes to be called "false gravity" or "imitation gravity" or "quasi-gravity".

Role in developing the idea of inertial frames

A continuing theme in classical mechanics has been the role of "absolute space". In the rotating bucket experiment Newton observed the shape of the surface of water in a bucket as the bucket was spun on a rope. At first the water is flat, then, as it acquires the same rotation as the bucket, it becomes parabolic. This shape is a consequence of centrifugal force, see subsection Potential energy above. Newton took this change as evidence that one could detect motion relative to "absolute space" experimentally, in this instance by looking at the shape of the surface of the water.

Later scientists found this view unwarranted: they pointed out (as did Newton) that the laws of mechanics were the same for all observers that differed only by uniform translation; that is, all observers that differed in motion only by a constant velocity. Hence, the "fixed stars" or "absolute space" was not preferred, but only one of a set of frames related by Galilean transformations.

By the end of the nineteenth century, some physicists had concluded that the concept of absolute space is not really needed...they used the law of inertia to define the entire class of inertial frames. Purged of the concept of absolute space, Newton's laws do single out the class of inertial frames of reference, but assert their complete equality for the description of all mechanical phenomena.

— Laurie M. Brown, Abraham Pais, A. B. Pippard: Twentieth Century Physics, pp. 256-257

The inadequacy of the notion of "absolute space" in Newtonian mechanics is spelled out by Blagojević:

• The existence of absolute space contradicts the internal logic of classical mechanics since, according to Galilean principle of relativity, none of the inertial frames can be singled out.
• Absolute space does not explain inertial forces since they are related to acceleration with respect to any one of the inertial frames.
• Absolute space acts on physical objects by inducing their resistance to acceleration but it cannot be acted upon.

— Milutin Blagojević: Gravitation and Gauage Symmetries, p. 5

Ultimately this notion of the transformation properties of physical laws between frames played a more and more central role. It was noted that accelerating frames exhibited "fictitious forces" like the centrifugal force. These forces did not behave under transformation like other forces, providing a means of distinguishing them. This peculiarity of these forces led to the names inertial forces, pseudo-forces or fictitious forces. In particular, fictitious forces did not appear at all in some frames: those frames differing from that of the fixed stars by only a constant velocity. In short, a frame tied to the "fixed stars" is merely a member of the class of "inertial frames", and absolute space is an unnecessary and logically untenable concept. The preferred, or "inertial frames", were identifiable by the absence of fictitious forces.

The effect of his being in the noninertial frame is to require the observer to introduce a fictitious force into his calculations….

— Sidney Borowitz and Lawrence A Bornstein in A Contemporary View of Elementary Physics, p. 138

The equations of motion in an non-inertial system differ from the equations in an inertial system by additional terms called inertial forces. This allows us to detect experimentally the non-inertial nature of a system.

— V. I. Arnol'd: Mathematical Methods of Classical Mechanics Second Edition, p. 129

The idea of an inertial frame was extended further in the special theory of relativity. This theory posited that all physical laws should appear of the same form in inertial frames, not just the laws of mechanics. In particular, Maxwell's equations should apply in all frames. Because Maxwell's equations implied the same speed of light in the vacuum of free space for all inertial frames, inertial frames now were found to be related not by Galilean transformations, but by Poincaré transformations, of which a subset is the Lorentz transformations. That posit led to many ramifications, including Lorentz contractions and relativity of simultaneity. Einstein succeeded, through many clever thought experiments, in showing that these apparently odd ramifications in fact had very natural explanation upon looking at just how measurements and clocks actually were used. That is, these ideas flowed from operational definitions of measurement coupled with the experimental confirmation of the constancy of the speed of light.

Later the general theory of relativity further generalized the idea of frame independence of the laws of physics, and abolished the special position of inertial frames, at the cost of introducing curved space-time. Following an analogy with centrifugal force (sometimes called "artificial gravity" or "false gravity"), gravity itself became a fictitious force, as enunciated in the principle of equivalence.

The principle of equivalence: There is no experiment observers can perform to distinguish whether an acceleration arises because of a gravitational force or because their reference frame is accelerating

— Douglas C. Giancoli Physics for Scientists and Engineers with Modern Physics, p. 155

In short, centrifugal force played a key early role in establishing the set of inertial frames of reference and the significance of fictitious forces, even aiding in the development of general relativity.

Applications

The operations of numerous common rotating mechanical systems are most easily conceptualized in terms of centrifugal force. For example: Template:Multicol

• A centrifugal governor regulates the speed of an engine by using spinning masses that move radially, adjusting the throttle, as the engine changes speed. In the reference frame of the spinning masses, centrifugal force causes the radial movement.
• A centrifugal clutch is used in small engine-powered devices such as chain saws, go-karts and model helicopters. It allows the engine to start and idle without driving the device but automatically and smoothly engages the drive as the engine speed rises. Inertial drum brake ascenders used in rock climbing and the inertia reels used in many automobile seat belts operate on the same principle.
• Centrifugal forces can be used to generate artificial gravity, as in proposed designs for rotating space stations. The Mars Gravity Biosatellite will study the effects of Mars-level gravity on mice with gravity simulated in this way.
• Spin casting and centrifugal casting are production methods that uses centrifugal force to disperse liquid metal or plastic throughout the negative space of a mold.

Template:Multicol-break

• Centrifuges are used in science and industry to separate substances. In the reference frame spinning with the centrifuge, the centrifugal force induces a hydrostatic pressure gradient in fluid-filled tubes oriented perpendicular to the axis of rotation, giving rise to large buoyant forces which push low-density particles inward. Elements or particles denser than the fluid move outward under the influence of the centrifugal force. This is effectively Archimedes' principle as generated by centrifugal force as opposed to being generated by gravity.
• Some amusement park rides make use of centrifugal forces. For instance, a Gravitron’s spin forces riders against a wall and allows riders to be elevated above the machine’s floor in defiance of Earth’s gravity.

Template:Multicol-end Nevertheless, all of these systems can also be described without requiring the concept of centrifugal force, in terms of motions and forces in an inertial frame, at the cost of taking somewhat more care in the consideration of forces and motions within the system.

See also

• Mechanics of planar particle motion
• Calculating relative centrifugal force
• Circular motion
• Coriolis force
• Coriolis effect (perception)
• Centripetal force
• Equivalence principle
• Bucket argument
• Euler force
• Folk physics
• Rotational motion
• Reactive centrifugal force
• Lamm equation
• Frame of reference
• Inertial frame of reference
• Fictitious force
• Lagrangian point
• Orthogonal coordinates
• Frenet-Serret formulas
• Statics
• Kinetics (physics)
• Kinematics
• Applied mechanics
• Analytical mechanics
• Dynamics (physics)
• Classical mechanics
• D'Alembert's principle
• Centrifuge
• Clairaut's theorem

Notes and references

1. By "absolute" is meant as seen in any inertial frame of reference; for example "absolute acceleration" or "absolute derivative".
2. The vector Ω has magnitude Ω equal to the rate of rotation and is directed along the axis of rotation according to the right-hand rule
3. John L. Synge (2007). Principles of Mechanics (Reprint of Second Edition of 1942 ed.). Read Books. p. 347. ISBN 1406746703.
4. Vladimir Igorević Arnolʹd (1989). Mathematical Methods of Classical Mechanics (2nd ed.). Springer. p. 130. ISBN 978-0-387-96890-2.
5. Cornelius Lanczos (1986). The Variational Principles of Mechanics (Reprint of Fourth Edition of 1970 ed.). Dover Publications. Chapter 4, §5. ISBN 0-486-65067-7. {{cite book}}: Unknown parameter |nopp= ignored (|no-pp= suggested) (help)
6. John R Taylor (2005). Classical Mechanics. University Science Books. p. 342. ISBN 1-891389-22-X.
7. LD Landau and LM Lifshitz (1976). Mechanics (Third ed.). Oxford: Butterworth-Heinemann. p. 128. ISBN 978-0-7506-2896-9.
8. Louis N. Hand, Janet D. Finch (1998). Analytical Mechanics. Cambridge University Press. p. 267. ISBN 0521575729.
9. Morton Tavel (2002). Contemporary Physics and the Limits of Knowledge. Rutgers University Press. p. 93. ISBN 0813530776. Noninertial forces, like centrifugal and Coriolis forces, can be eliminated by jumping into a reference frame that moves with constant velocity, the frame that Newton called inertial.
10. John Robert Taylor (2004). Classical Mechanics. Sausalito CA: University Science Books. Chapter 9, pp. 327 ff. ISBN 189138922X. {{cite book}}: Unknown parameter |nopp= ignored (|no-pp= suggested) (help)
11. Stephen T. Thornton & Jerry B. Marion (2004). Classical Dynamics of Particles and Systems (5th ed.). Belmont CA: Brook/Cole. Chapter 10. ISBN 0534408966. {{cite book}}: Unknown parameter |nopp= ignored (|no-pp= suggested) (help); line feed character in |author= at position 22 (help)
12. Federal Aviation Administration (2007). Pilot's Encyclopedia of Aeronautical Knowledge. Oklahoma City OK: Skyhorse Publishing Inc. Figure 3-21. ISBN 1602390347. {{cite book}}: Unknown parameter |nopp= ignored (|no-pp= suggested) (help)
13. Richard Hubbard (2000). Boater's Bowditch: The Small Craft American Practical Navigator. NY: McGraw-Hill Professional. p. 54. ISBN 0071361367.
14. Lawrence K. Wang, Norman C. Pereira (1979). Handbook of Environmental Engineering: Air and Noise Pollution Control. Humana Press. p. 63. ISBN 0896030016.
15. Lee M. Grenci, Jon M. Nese (2001). A World of Weather: Fundamentals of Meteorology. Kendall Hunt. p. 272. ISBN 0787277169.
16. Peter Ryder (2007). Classical Mechanics. Aachen Shaker. p. 78-79. ISBN 978-3-8322-6003-3.
17. ^ Robert Daniel Carmichael (1920). The Theory of Relativity. John Wiley & Sons. p. 78. Cite error: The named reference "Carmichael" was defined multiple times with different content (see the help page).
18. Hans J. Weber & George B. Arfken (2003). Essential mathematical methods for physicists. Academic Press. p. 79. ISBN 0120598779.
19. Louis N. Hand & Janet D. Finch (1998). Finch Analytical Mechanics. Cambridge UK: Cambridge University Press. p. 267. ISBN 0521575729. {{cite book}}: Check |url= value (help)
20. John Robert Taylor (2004). Classical Mechanics. Sausalito CA: University Science Books. p. 343-344. ISBN 189138922X.
21. Georg Joos & Ira M. Freeman (1986). Theoretical Physics. New York: Courier Dover Publications. p. 233. ISBN 0486652270.
22. John Robert Taylor (2004). Classical Mechanics. Sausalito CA: University Science Books. p. 348-349. ISBN 189138922X.
23. The vector cross product of the two orthogonal vectors Ω and R is a vector of magnitude equal to the product of their magnitudes, namely Ω R = v_rot, and with direction given by the right-hand rule, in this case found by aligning the thumb with Ω, the index finger with R, and the middle finger normal to these two fingers points in the direction of −v_rot.
24. Louis Bevier Spinney (1911). A Text-book of Physics. Macmillan Co. p. 47-49.
25. Arthur Beiser & George J. Hademenos (2003). Applied physics: Based on Schaum's Outline of Theory and Problems of Applied Physics (Third Edition). McGraw-Hill Professional. p. 37. ISBN 0071398783.
26. Burgel, B. (1967). "Centrifugal Force". American Journal of Physics. 35: 649. doi:10.1119/1.1974204.
27. John Robert Taylor (2004). pp. 349ff. Sausalito, Calif.: Univ. Science Books. ISBN 189138922X.
28. Dionysius Lardner (1877). Mechanics. Oxford University Press. p. 150.
29. John Robert Taylor (2005). Classical Mechanics. University Science Books. p. 349. ISBN 189138922X.
30. Robin McIlveen (1991). Fundamentals of Weather and Climate. Routledge. p. 187. ISBN 0748740791.
31. J. P. Den Hartog (1961). Mechanics (Corrected reprint of 1948 First ed.). Courier Dover Publications. p. 304. ISBN 0486607542.
32. Donald A. Danielson (2003). Vectors and Tensors in Engineering and Physics. Westview Press. p. p.86. ISBN 0813340802. {{cite book}}: |page= has extra text (help)
33. Denison Olmsted & Ebenezer Strong Snell (1861). An Introduction to Natural Philosophy. Collins & Brother. p. 133.
34. As seen by the inertial observer, the plane also may accelerate along its path (dv / dt = ds / dt > 0). For the pilot this acceleration introduces another fictitious force: the Euler force.
35. Carl D. Murray, S. F. Dermott (1999). Solar system dynamics. Cambridge University Press. Chapter 2. ISBN 0521575974. {{cite book}}: Unknown parameter |nopp= ignored (|no-pp= suggested) (help)
36. Oliver Dimon Kellogg (1954). Foundations of Potential Theory (Reprint of 1929 ed.). Courier Dover Publications. p. 156. ISBN 0486601447.
37. Yves Talpaert (2006). Mechanics in Differential Geometry. Walter de Gruyter. p. 485. ISBN 9067644579.
38. Dean C. Karnopp & Donald L. Margolis (2007). Engineering Applications of Dynamics. Wiley. p. 6. ISBN 0470112662.
39. See Jeremy B. Tatum Celestial Mechanics Chapter 16 or Jeremy B. Tatum Celestial Mechanics , University of Victoria, p. 2
40. David Morin (2008). Introduction to Classical Mechanics. Cambridge University Press. p. 283-284. ISBN 0521876222.
41. Herbert Goldstein (1950). Classical Mechanics. Addison-Wesley. Chapter 3, p. 61. {{cite book}}: Unknown parameter |nopp= ignored (|no-pp= suggested) (help)
42. Kenneth Ray Meyer (1999). Periodic Solutions of the N-body Problem. Springer. p. 32. ISBN 3540666303.
43. The Relativization of Centrifugal Force Author(s): Domenico Bertoloni Meli Source: Isis, Vol. 81, No. 1, (Mar., 1990), pp. 23-43 Published by: The University of Chicago Press on behalf of The History of Science Society.
44. ^ "Newton, Sir Isaac". Retrieved 2008-05-25.
45. Soshichi Uchii (October 9, 2001). "Inertia". Retrieved 2008-05-25.
46. M. Novello, Matt Visser & G. E. Volovik (2002). Artificial black holes. World Scientific. p. 200. ISBN 9810248075.
47. Laurie M. Brown, Abraham Pais & A. B. Pippard (1995). Twentieth Century Physics. CRC Press. p. 256-257. ISBN 0750303107.
48. Milutin Blagojević (2002). Gravitation and Gauge Symmetries. CRC Press. p. 5. ISBN 0750307676.
49. The idea of transformation properties of physical laws under various transformations is a central topic in modern physics, related to such basic concepts as conservation laws like conservation of energy and momentum through Noether's theorem. See, for example, Harvey R. Brown (2005). Physical Relativity. Oxford University Press. p. 180. ISBN 0199275831., and Gennady Gorelik (Yuri Balashov, Vladimir Pavlovich Vizgin: editiors) (2002). Einstein Studies in Russia. Birkhäuser. p. The problem of conservation laws and the Poincare quasigroup in general relativity; pp. 17 ff. ISBN 0817642633. and Peter Mittelstaedt & Paul Weingartner (2005). Laws of Nature. Springer. p. 80. ISBN 3540240799.
50. Milton A. Rothman (1989). Discovering the Natural Laws: The Experimental Basis of Physics. Courier Dover Publications. p. 23. ISBN 0486261786.
51. Sidney Borowitz & Lawrence A. Bornstein (1968). A Contemporary View of Elementary Physics. McGraw-Hill. p. 138. ASIN B000GQB02A.
52. V. I. Arnol'd (1989). Mathematical Methods of Classical Mechanics. Springer. p. 129. ISBN 978-0-387-96890-2.
53. Hans Christian Von Baeyer (2001). The Fermi Solution: Essays on science (Reprint of 1993 ed.). Courier Dover Publications. p. 78. ISBN 0486417077.
54. Douglas C. Giancoli (2007). Physics for Scientists and Engineers with Modern Physics. Pearson Prentice Hall. p. 155. ISBN 0131495089.

Further reading

• Newton's description in Principia
• Centrifugal reaction force - Columbia electronic encyclopedia
• M. Alonso and E.J. Finn, Fundamental university physics, Addison-Wesley
• Centripetal force vs. Centrifugal force - from an online Regents Exam physics tutorial by the Oswego City School District
• Centrifugal force acts inwards near a black hole
• Centrifugal force at the HyperPhysics concepts site
• A list of interesting links
• Part of a high school course on astronomy, Newtonian mechanics and spaceflight by David P. Stern

External links

• Motion over a flat surface Java physlet by Brian Fiedler (from School of Meteorology at the University of Oklahoma) illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and from a non-rotating point of view.
• Motion over a parabolic surface Java physlet by Brian Fiedler (from School of Meteorology at the University of Oklahoma) illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and as seen from a non-rotating point of view.
• Animation clip showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.
• Centripetal and Centrifugal Forces at MathPages
• Centrifugal Force at h2g2
• What is a centrifuge?
• John Baez: Does centrifugal force hold the Moon up?
• XKCD demonstrates the life and death importance of centrifugal force

• Fictitious forces
• Force
• Mechanics
• Rotation