Misplaced Pages

This is an old revision of this page, as edited by 194.254.137.115 (talk) at 08:10, 5 December 2011. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Shifted Gompertz

Probability density function
Cumulative distribution function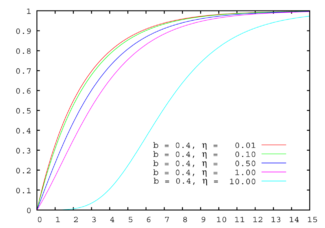
Parameters	${\displaystyle b>0}$ scale (real) ${\displaystyle \eta >0}$ shape (real)
Support	${\displaystyle x\in [0,\infty )\!}$
PDF	${\displaystyle be^{-bx}e^{-\eta e^{-bx}}\left}$
CDF	${\displaystyle \left(1-e^{-bx}\right)e^{-\eta e^{-bx}}}$
Mean	${\displaystyle (-1/b)\{\mathrm {E} -\ln(\eta )\}\,}$ where ${\displaystyle X=\eta e^{-bx}\,}$ and ${\displaystyle {\begin{aligned}\mathrm {E} =&\!\!\int _{0}^{\eta }\!\!\!\!e^{-X}dX\\&-1/\eta \!\!\int _{0}^{\eta }\!\!\!\!Xe^{-X}dX\end{aligned}}}$
Mode	${\displaystyle 0\,}$ for ${\displaystyle \eta \leq 0.5\,}$, ${\displaystyle (-1/b)\ln(z^{\star })\,}$ for ${\displaystyle \eta >0.5\,}$where${\displaystyle z^{\star }=/(2\eta )}$
Variance	${\displaystyle (1/b^{2})(\mathrm {E} \{^{2}\}-(\mathrm {E} )^{2})\,}$ where ${\displaystyle X=\eta e^{-bx}\,}$ and ${\displaystyle {\begin{aligned}\mathrm {E} \{^{2}\}=&\!\!\int _{0}^{\eta }\!\!\!\!e^{-X}^{2}dX\\&-1/\eta \!\!\int _{0}^{\eta }\!\!\!\!Xe^{-X}^{2}dX\end{aligned}}}$

The shifted Gompertz distribution is the distribution of the largest of two independent random variables one of which has an exponential distribution with parameter b and the other has a Gumbel distribution with parameters ${\displaystyle \eta }$ and b. In its original formulation the distribution was expressed referring to the Gompertz distribution instead of the Gumbel distribution but, since the Gompertz distribution is a reverted Gumbel distribution truncated at zero, the labelling can be considered as accurate. It has been used as a model of adoption of innovations. It was proposed by Bemmaor (1994).

Specification

Probability density function

The probability density function of the shifted Gompertz distribution is:

${\displaystyle f(x;b,\eta )=be^{-bx}e^{-\eta e^{-bx}}\left\mathrm {for} x\geq 0.\,}$

where ${\displaystyle b>0}$ is the scale parameter and ${\displaystyle \eta >0}$ is the shape parameter of the shifted Gompertz distribution.

Cumulative distribution function

The cumulative distribution function of the shifted Gompertz distribution is:

${\displaystyle F(x;b,\eta )=\left(1-e^{-bx}\right)e^{-\eta e^{-bx}}\mathrm {for} {\text{ for }}x\geq 0.\,}$

Properties

The shifted Gompertz distribution is right-skewed for all values of ${\displaystyle \eta }$. It is more flexible than the Gumbel distribution.

Shapes

The shifted Gompertz density function can take on different shapes depending on the values of the shape parameter ${\displaystyle \eta }$:

• ${\displaystyle \eta \leq 0.5\,}$ the probability density function has its mode at 0.
• ${\displaystyle \eta >0.5\,}$ the probability density function has its mode at

${\displaystyle {\text{mode}}=-{\frac {\ln(z^{\star })}{b}}\,\qquad 0<z^{\star }<1}$

where ${\displaystyle z^{\star }\,}$ is the smallest root of

${\displaystyle \eta ^{2}z^{2}-\eta (3+\eta )z+\eta +1=0\,,}$

which is

${\displaystyle z^{\star }=/(2\eta ).}$

Related distributions

If ${\displaystyle \eta }$ varies according to a gamma distribution with shape parameter ${\displaystyle \alpha }$ and scale parameter ${\displaystyle \beta }$ (mean = ${\displaystyle \alpha \beta }$), the cumulative distribution function is Gamma/Shifted Gompertz (G/SG). When ${\displaystyle \alpha }$ is equal to one, the G/SG reduces to the Bass model.

See also

• Gumbel distribution
• Generalized extreme value distribution
• Mixture model
• Bass model
• Gompertz distribution

References

• Bemmaor, Albert C. (1994). "Modeling the Diffusion of New Durable Goods: Word-of-Mouth Effect Versus Consumer Heterogeneity". In G. Laurent, G.L. Lilien & B. Pras (ed.). Research Traditions in Marketing. Boston: Kluwer Academic Publishers. pp. 201–223. ISBN 0792393880.
• Chandrasekaran, Deepa; Tellis, Gerard J. (2007). "A Critical Review of Marketing Research on Diffusion of New Products". In Naresh K. Malhotra (ed.). Review of Marketing Research. Vol. 3. Armonk: M.E. Sharpe. pp. 39–80. ISBN 978-0-7656-1306-6.
• Jimenez, Fernando; Jodra, Pedro (2009). "A Note on the Moments and Computer Generation of the Shifted Gompertz Distribution". Communications in Statistics - Theory and Methods. 38 (1): 78–89. doi:10.1080/03610920802155502.
• Van den Bulte, Christophe; Stremersch, Stefan (2004). "Social Contagion and Income Heterogeneity in New Product Diffusion: A Meta-Analytic Test". Marketing Science. 23 (4): 530–544. doi:10.1287/mksc.1040.0054.

• Continuous distributions