Misplaced Pages

This is an old revision of this page, as edited by 136.186.1.118 (talk) at 06:21, 20 April 2006 (how is theorem defined in this instance?). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

In electrical engineering, the maximum power (transfer) theorem states that to obtain maximum power from a source with a fixed internal resistance the resistance of the load must be made the same as that of the source.

The theorem applies only when the source resistance is fixed. If the source resistance were variable (but the load resistance fixed), maximum power would be transferred to the load simply by setting the source resistance to zero. Raising the source impedance to match the load would, in this case, reduce power transfer. This is the case when driving a load such as a loudspeaker with a modern amplifier. In this case, the load presented by the loudspeaker is fixed (typically, 8 ohms for home audio) and maximum power occurs with an impedance bridging connection. This type of connection also serves to maximize control of the speaker cone (due to high damping factor), which serves to lower distortion.

Maximising power transfer versus power efficiency

The theorem was originally misunderstood (notably by Joule) to imply that a system consisting of an electric motor driven by a battery could not be more than 50% efficient, since the power lost as heat in the battery would always be equal to the power delivered to the motor. In 1880 this assumption was shown to be false by either Edison or his colleague Francis Robbins Upton, who realized that the theorem could be sidestepped by making the resistance of the source (whether a battery or a dynamo) close to zero. Using this new understanding, they obtained an efficiency of about 90%, and proved that the electric motor was a practical alternative to the heat engine.

The condition of maximum power transfer does not result in maximum efficiency. If we define the efficiency ${\displaystyle \eta }$ as the ratio of power dissipated by the load to power developed by the source, then it is straightforward to calculate from the above circuit diagram that

${\displaystyle \eta ={R_{\mathrm {load} } \over {R_{\mathrm {load} }+R_{\mathrm {source} }}}={1 \over {1+{R_{\mathrm {source} } \over R_{\mathrm {load} }}}}}$

Consider three particular cases:

• If ${\displaystyle R_{\mathrm {load} }=R_{\mathrm {source} }}$, then ${\displaystyle \eta =0.5}$.
• If ${\displaystyle R_{\mathrm {load} }=\infty }$, then ${\displaystyle \eta =1}$.
• If ${\displaystyle R_{\mathrm {load} }=0}$, then ${\displaystyle \eta =0}$.

The efficiency is only 50% when maximum power transfer is achieved, but approaches 100% as the load resistance approaches infinity (though the total power level tends towards zero). When the load resistance is zero, all the power is consumed inside the source (the power dissipated in a short circuit is zero) so the efficiency is zero.

Impedance matching

A related concept is reflectionless impedance matching. In radio, transmission lines, and other electronics, there is often a requirement to match the source impedance (such as a transmitter) to the load impedance (such as an antenna) to avoid reflections in the transmission line.

In reactive circuits

The theorem also applies where the source and/or load are not totally resistive. This invokes a refinement of the theorem which says that any reactive components of source and load should be of equal magnitude but opposite phase. (See below for a derivation.) This means that the source and load impedances should be complex conjugates of each other. In the case of purely resistive circuits, the two concepts are identical. However, physically realizable sources and loads are not usually totally resistive, having some inductive or capacitive components, and so practical applications of this theorem, under the name of complex conjugate impedance matching, do, in fact, exist.

If the source is totally inductive (capacitive), then a totally capacitive (inductive) load, in the absence of resistive losses, would receive 100% of the energy from the source but send it back after a quarter cycle. The resultant circuit is nothing other than a resonant LC circuit in which the energy continues to oscillate to and fro. This is called reactive power. Power factor correction(where an inductive reactance is used to "balance out" a capacitive one), is essentially the same idea as conjugate impedance matching although it is done for entirely different reasons.

For a fixed reactive source, the maximum power theorem maximizes the real power (P) delivered to the load by complex conjugate matching the load to the source.

For a fixed reactive load, power factor correction minimizes the apparent power (S) (and unnecessary current) conducted by the transmission lines, while maintaining the same amount of real power transfer. This is done by adding a reactance to the load to balance out the load's own reactance, changing the reactive load impedance into a resistive load impedance.

Proof of theorem for resistive circuits

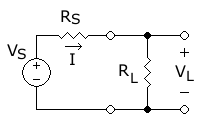
In the diagram opposite, power is being transferred from the source, with voltage ${\displaystyle V}$ and fixed source resistance ${\displaystyle R_{\mathrm {S} }}$, to a load with resistance ${\displaystyle R_{\mathrm {L} }}$, resulting in a current ${\displaystyle I}$. ${\displaystyle I}$ is simply the source voltage divided by the total circuit resistance:

${\displaystyle I={V \over R_{\mathrm {S} }+R_{\mathrm {L} }}}$

The power ${\displaystyle P_{\mathrm {L} }}$ dissipated in the load is the square of the current multiplied by the resistance:

${\displaystyle P_{\mathrm {L} }=I^{2}R_{\mathrm {L} }={{\left({V \over {R_{\mathrm {S} }+R_{\mathrm {L} }}}\right)}^{2}}R_{\mathrm {L} }={{V^{2}} \over {R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}}}$

We could calculate the value of ${\displaystyle R_{\mathrm {L} }}$ for which this expression is a maximum, but it is easier to calculate the value of ${\displaystyle R_{\mathrm {L} }}$ for which the denominator

${\displaystyle R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}$

is a minimum. The result will be the same in either case. Differentiating with respect to ${\displaystyle R_{\mathrm {L} }}$:

${\displaystyle {d \over {dR_{\mathrm {L} }}}\left({R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}\right)=-R_{\mathrm {S} }^{2}/R_{\mathrm {L} }^{2}+1}$

For a maximum or minimum, the first derivative is zero, so

${\displaystyle {R_{\mathrm {S} }^{2}/R_{\mathrm {L} }^{2}}=1}$

or

${\displaystyle R_{\mathrm {L} }=\pm R_{\mathrm {S} }}$

In practical resistive circuits, ${\displaystyle R_{\mathrm {S} }}$ and ${\displaystyle R_{\mathrm {L} }}$ are both positive. To find out whether this solution is a minimum or a maximum, we must differentiate again:

${\displaystyle {{d^{2}} \over {dR_{\mathrm {L} }^{2}}}\left({R_{\mathrm {S} }^{2}/R_{\mathrm {L} }+2R_{\mathrm {S} }+R_{\mathrm {L} }}\right)={2R_{\mathrm {S} }^{2}}/{R_{\mathrm {L} }^{3}}}$

This is positive for positive values of ${\displaystyle R_{\mathrm {S} }}$ and ${\displaystyle R_{\mathrm {L} }}$, showing that the denominator is a minimum, and the power is therefore a maximum, when

${\displaystyle R_{\mathrm {S} }=R_{\mathrm {L} }}$

For reactive impedances

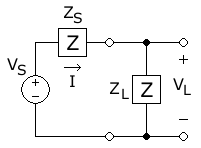
In this diagram, AC power is being transferred from the source, with phasor magnitude voltage ${\displaystyle |V_{\mathrm {S} }|}$ (peak voltage) and fixed source impedance ${\displaystyle Z_{\mathrm {S} }}$, to a load with impedance ${\displaystyle Z_{\mathrm {L} }}$, resulting in a phasor magnitude current ${\displaystyle |I|}$. ${\displaystyle |I|}$ is simply the source voltage divided by the total circuit impedance:

${\displaystyle |I|={|V_{\mathrm {S} }| \over Z_{\mathrm {S} }+Z_{\mathrm {L} }}}$

The average power ${\displaystyle P_{\mathrm {L} }}$ dissipated in the load is the square of the current multiplied by the resistive portion of the load impedance:

${\displaystyle P_{\mathrm {L} }}$	${\displaystyle =I_{\mathrm {rms} }^{2}R_{\mathrm {L} }={1 \over 2}|I|^{2}R_{\mathrm {L} }={1 \over 2}{{\left({|V_{\mathrm {S} }| \over {Z_{\mathrm {S} }+Z_{\mathrm {L} }}}\right)}^{2}}R_{\mathrm {L} }}$
	${\displaystyle ={1 \over 2}{{|V_{\mathrm {S} }|^{2}R_{\mathrm {L} }} \over {(R_{\mathrm {S} }+R_{\mathrm {L} })^{2}+(X_{\mathrm {S} }+X_{\mathrm {L} })^{2}}}}$

We could calculate the values of ${\displaystyle R_{\mathrm {L} }}$ and ${\displaystyle X_{\mathrm {L} }}$ (since ${\displaystyle V_{\mathrm {S} }}$, ${\displaystyle R_{\mathrm {S} }}$, and ${\displaystyle X_{\mathrm {S} }}$ are fixed) for which this expression is a maximum, but it is easier to calculate the values for which the denominator

${\displaystyle (R_{\mathrm {S} }+R_{\mathrm {L} })^{2}+(X_{\mathrm {S} }+X_{\mathrm {L} })^{2}}$

is a minimum. The result will be the same in either case. Since reactances can be negative, the reactive term is easily minimized to zero by making

${\displaystyle X_{\mathrm {L} }=-X_{\mathrm {S} }}$

The power equation is now reduced to:

${\displaystyle P_{\mathrm {L} }={1 \over 2}{{|V_{\mathrm {S} }|^{2}R_{\mathrm {L} }} \over {(R_{\mathrm {S} }+R_{\mathrm {L} })^{2}}}}$

This is the same form as above, and the maximizing condition ${\displaystyle R_{\mathrm {L} }=R_{\mathrm {S} }}$ can be found in the same way.

The combination of conditions

• ${\displaystyle R_{\mathrm {L} }=R_{\mathrm {S} }}$
• ${\displaystyle X_{\mathrm {L} }=-X_{\mathrm {S} }}$

can be concisely written with a complex conjugate (the *) as:

${\displaystyle Z_{\mathrm {S} }=Z_{\mathrm {L} }^{*}}$

References

• H.W. Jackson (1959) Introduction to Electronic Circuits, Prentice-Hall.

External links

• The complex conjugate matching false idol
• Conjugate matching versus reflectionless matching (PDF) taken from Electromagnetic Waves and Antennas
• The Spark Transmitter. 2. Maximising Power, part 1.
• Maximum power for AC impedances
• Jacobi's theorem - unconfirmed claim that theorem was discovered by Moritz Jacobi
• MH Jacobi Biographical notes

See also

Maximum power principle

• Physics theorems
• Electrical engineering