Misplaced Pages

Major thirds tuning

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.

This is an old revision of this page, as edited by Kiefer.Wolfowitz (talk | contribs) at 09:38, 28 January 2013 (→Open chords and beginning players: (for example, acoustic-electric guitars without amplification).). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Revision as of 09:38, 28 January 2013 by Kiefer.Wolfowitz (talk | contribs) (→Open chords and beginning players: (for example, acoustic-electric guitars without amplification).)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)

Major thirds
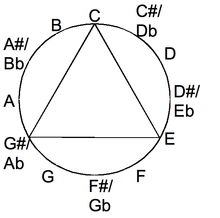An equilateral triangle's corners represent the equally spaced notes of a major-thirds tuning, here E-C-G♯. The triangle is circumscribed by the chromatic circle, which lists the 12 notes of the octave.Each major-thirds tuning packs the octave's 12 notes into 3 strings' 4 frets.
Basic information
AliasesAll-thirds (M3) tuning
Augmented tuning
IntervalMajor third
Semitones4
Example(s)G♯-C-E-G♯-C-E
Advanced information
RepetitionAfter 3 strings
AdvantagesOctave on 4 frets,
Major–minor chords on 2
Regular tunings (semitones)
Trivial (0)
Minor thirds (3)
Major thirds (4)
All fourths (5)
Augmented fourths (6)
New standard (7, 3)
All fifths (7)
Minor sixths (8)
Guitar tunings

Among alternative tunings for guitar, a major-thirds tuning is a regular tuning in which each interval between successive open strings is a major third ("M3" in musical abbreviation). Other names for major-thirds tuning include major-third tuning, M3 tuning, all-thirds tuning, and augmented tuning. By definition, a major-third interval separates two notes that differ by exactly four semitones (one-third of the twelve-note octave).

The Spanish guitar's tuning mixes four perfect fourths (five semitones) and one major-third, the latter occurring between the G and B strings:

E-A-D-G-B-E.

This tuning, which is used for acoustic and electric guitars, is called "standard" in English, a convention that is followed in this article. While standard tuning is irregular, mixing four fourths and one major third, M3 tunings are regular: Only major-third intervals occur between the successive strings of the M3 tunings, for example, the open augmented C tuning

G♯-C-E-G♯-C-E.

For each M3 tuning, the open strings form an augmented triad in two octaves.

For guitars with six strings, every major-third tuning repeats its three open-notes in two octaves, so providing many options for fingering chords. By repeating open-string notes and by having uniform intervals between strings, major-thirds tuning simplifies learning by beginners. These features also facilitate advanced guitarists' improvisation, precisely the aim of jazz-guitarist Ralph Patt when he invented major-thirds tuning between 1963 and 1964.

Avoiding standard tuning's irregular intervals

The fretboard of major-thirds tuning is segmented into four-fret intervals, frets 0–3, 4–7, and 8–11; the natural notes are labeled.
M3 tuning partitions its fretboard into four-fret segments.

In standard tuning, the successive open-strings mix two types of intervals, four perfect-fourths and the major third between the G and B strings:

E-A-D-G-B-E.

Of course, only major thirds occur as open-string intervals for major-thirds tuning, which is also called "major-third tuning", "all-thirds tuning", and "M3 tuning". A popular M3 tuning has the open strings

G♯-C-E-G♯-C-E,

in which the low G♯ is a major third above the low E of standard tuning. Consequently, a seventh string for the low E is often added to restore the standard E-E range. While M3 tuning can use standard sets of guitar strings, specialized string gauges have been recommended. Besides this M3 tuning, which has the open notes {G♯, C, E}, there are exactly three other M3 tunings, which have distinct sets of open-note pitch classes. The other major-thirds tunings respectively have the open notes {A, C♯, F}, {A♯, D, F♯}, and {B, D♯, G}. For six-string guitars, the M3 tuning

F♯-A♯-D-F♯-A♯-D

loses the two lowest semitones on the low-E string and the two highest semitones from the high-E string in standard tuning; it can use string sets for standard tuning.

Properties

Minor, major, and seventh chords are played with the same shape on two-three consecutive frets.
Shifting a chord by three strings raises it by one octave.
The C major chord and its first and second inversions. In the first inversion, the C note has been raised 3 strings on the same fret. In the second inversion, both the C note and the E note have been raised 3 strings on the same fret.
Chords are inverted by shifting notes by three strings on their original frets.

The properties of major-thirds tunings can be briefly summarized before they are discussed in detail. Major-thirds tunings require less hand-stretching than other tunings, because each M3 tuning packs the octave's twelve notes into four consecutive frets. The major-third intervals allow major chords and minor chords to be played with two–three consecutive fingers on two consecutive frets. Every major-thirds tuning is regular and repetitive, two properties that facilitate learning by beginners and improvisation by advanced guitarists.

Four frets for the four fingers

In major-thirds tuning, the chromatic scale is arranged on three consecutive strings in four consecutive frets. This four-fret arrangement facilitates the left-hand technique for classical (Spanish) guitar: For each hand position of four frets, the hand is stationary and the fingers move, each finger being responsible for exactly one fret. Consequently, three hand-positions (covering frets 1–4, 5–8, and 9–12) partition the fingerboard of classical guitar, which has exactly 12 frets.

Only two or three frets are needed for the guitar chords—major, minor, and dominant sevenths—which are emphasized in introductions to guitar-playing and to the fundamentals of music. Each major and minor chord can be played on exactly two successive frets on exactly three successive strings, and therefore each needs only two fingers. Other chords—seconds, fourths, sevenths, and ninths—are played on only three successive frets. For fundamental-chord fingerings, major-thirds tuning's simplicity and consistency are not shared by standard tuning, whose seventh-chord fingering is discussed at the end of this section.

Repetition

Each major-thirds tuning repeats its open-notes after every two strings, which results in two copies of the three open-strings' notes, each in a different octave. This repetition again simplifies the learning of chords and improvisation. This advantage is not shared by two popular regular-tunings, all-fourths and all-fifths tuning.

Chord inversion is especially simple in major-thirds tuning. Chords are inverted simply by raising one or two notes three strings. The raised notes are played with the same finger as the original notes. Thus, major and minor chords are played on two frets in M3 tuning even when they are inverted. In contrast, inversions of chords in standard tuning require three fingers on a span of four frets, in standard tuning, the shape of inversions depends on the involvement of the irregular major-third.

Regular musical-intervals

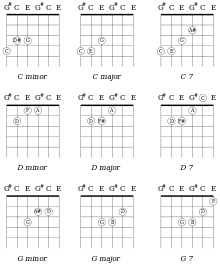
C major chords in standard and M3 tunings

In each regular tuning, the musical intervals are the same for each pair of consecutive strings. Other regular tunings include all-fourths, augmented-fourths, and all-fifths tunings. For each regular tuning, chord patterns may be moved around the fretboard, a property that simplifies beginners' learning of chords and that simplifies advanced players' improvisation.

In contrast, chords cannot be shifted around the fretboard in standard tuning, which requires four chord-shapes for the major chords: There are separate fingerings for chords having root notes on one of the four strings three–six.

Shifting chords: Vertical and diagonal

The repetition of the major-thirds tuning enables notes and chords to be raised one octave by being vertically shifted by three strings. Notes and chords may be shifted diagonally in major-thirds tuning, by combining a vertical shift of one string with a horizontal shift of four frets: "Like all regular tunings, chords in the major third tuning can be moved across the fretboard (ascending or descending a major third for each string)...."

In standard tuning, playing scales of one octave requires three patterns, which depend on the string of the root note. Chords cannot be shifted diagonally without changing finger-patterns. Standard tuning has four finger-patterns for musical intervals, four forms for basic major-chords, and three forms for the inversion of the basic major-chords.

Open chords and beginning players

Major-thirds tunings are unconventional open tunings, in which the open strings form an augmented triad; in M3 tunings, the augmented fifth replaces the perfect fifth of the major triad, which is used in conventional open-tunings. Consequently M3 tunings are also called (open) augmented-fifth tunings (in French "La guitare #5, majeure quinte augmentée").

Augmented triads
Chord Root Major third Augmented fifth
Faug F A C♯
F♯aug F♯ A♯ Cdouble sharp (D)
G♭aug G♭ B♭ D
G♯aug G♯ B♯ (C) Ddouble sharp (E)

Instructional literature uses standard tuning. Traditionally a course begins with the hand in first position, that is, with the left-hand covering frets 1–4. Beginning players first learn open chords belonging to the major keys C, G, and D. Guitarists who play mainly open chords in these three major-keys and their relative minor-keys (Am, Em, Bm) may prefer standard tuning over an M3 tuning. In particular, hobbyists playing folk music around a campfire are well served by standard tuning. Such hobbyists may also play major-thirds tuning, which also has many open chords with notes on five or six strings; chords with five-six strings have greater volume than chords with three-four strings and so are useful for acoustic guitars (for example, acoustic-electric guitars without amplification).

Intermediate guitarists do not limit themselves to one hand-position, and consequently open chords are only part of their chordal repertoire. In contemporary music, master guitarists "think diagonally and move up and down the strings"; fluency on the entire fretboard is needed particularly by guitarists playing jazz. According to its inventor, Ralph Patt, major-thirds tuning

"makes the hard things easy and the easy things hard. This is never going to take the place of folk guitar, and it's not meant to. For difficult music, and for where we are going in free jazz and even the old be-bop jazz, this is a much easier way to play."

Left-handed chords

Main article: Left-handed tuning

Major-thirds tuning is closely related to minor-sixths tuning, which is the regular tuning that is based on the minor sixth, the interval of eight semitones. Either ascending by a major third or by descending by a minor sixth, one arrives at the same pitch class, the same note representing pitches in different octaves. Intervals paired like the pair of major-third and minor-sixth intervals are termed "inverse intervals" in the theory of music. Consequently, chord charts for minor-sixths tunings may be used for left-handed major-thirds tunings; conversely, chord charts for major-thirds tunings may be used for left-handed minor-sixths tunings.

Additional discussion of standard tuning: Fingering seventh chords

In standard tuning, the C7 chord on frets 3–8 is difficult to play.

In contrast, standard tuning requires more hand-stretching or alterations of basic chords, for example of dominant seventh chords. By definition, a dominant seventh is a four-note chord combining a major chord and a minor seventh. For example, the C7 dominant seventh chord concatenates the C-major chord (C, E, G) with B♭. In standard tuning, the C7 chord (C, E, G, B♭) spans six frets (3–8); such seventh chords "contain some pretty serious stretches in the left hand". An illustration shows this C7 chord (C, E, G, B♭) , which would be extremely difficult to play in standard tuning, besides the open-position C7 chord that is conventional in standard tuning: This open-position C7 chord is termed a second-inversion C7 drop 2 chord (C, G, B♭, E), because the second-highest note (C) in the second-inversion C7 chord (G, B♭, C, E) is lowered by an octave.

History

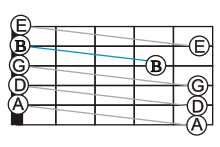
A guitar fretboard with line-segments connecting the successive open-string notes of standard tuning
Standard tuning's mixture of one major-third and four perfect-fourths did not meet Ralph Patt's needs for improvisation, so he invented M3 tuning.
Main article: Ralph Patt

Major-thirds tuning was introduced in 1964 by jazz-guitarist Ralph Patt. He was studying with Gunther Schuller, whose twelve-tone technique was invented for atonal composition by his teacher, Arnold Schoenberg. Patt was also inspired by the free jazz of Ornette Coleman and John Coltrane. Seeking a guitar-tuning that would facilitate improvisation using twelve-tones, he introduced major-thirds tuning by 1964, perhaps in 1963. To achieve the E-E open-string range of standard (Spanish) tuning, Patt started using seven-string guitars in 1963, before settling on eight-string guitars with high G♯ (equivalently A♭) as their highest open-notes. Patt used major-thirds tuning during all of his work as a session musician after 1965 in New York. Patt developed a webpage with extensive information about major-thirds tuning.

See also

  • Non-Spanish classical guitars used open tunings that approximate M3 tunings:
    • English: Its open-C tuning C-E-G-C-E-G approximates C-E-G♯-C-E-G♯.
    • Russian: Its 7-string open-G tuning G-B-D-G-B-D-G approximates G-B-D♯-G-B-D♯-G.

References

Footnotes

  1. ^ Classical guitars have 12 frets, while steel-string acoustics have 14 or more (Denyer 1992, p. 45). Electrical guitars have more frets, for example 20 (Denyer 1992, p. 77).
  2. ^ The illustration designates B♭ by its enharmonic equivalent, A♯.

Citations

  1. ^ Sethares (2001, "The major third tuning" (pp. 56–57), p. 56)
  2. ^ Peterson (2002, pp. 36–37)
  3. ^ Kirkeby (2012)
  4. ^ Peterson (2002, p. 36)
  5. ^ Griewank (2010, p. 3)
  6. ^ Patt, Ralph (4 April 2004). "Tuning in all thirds". rec.music.makers.guitar.jazz. Retrieved 10 December 2012. {{cite web}}: Invalid |ref=harv (help)
  7. ^ Griewank (2010, p. 1)
  8. ^ Griewank (2010, p. 4)
  9. ^ Peterson (2002, p. 37)
  10. Kirkeby (2012, "Strings")
  11. ^ Griewank (2010, p. 9)
  12. ^ Griewank (2010, p. 2)
  13. ^ Sethares (2001, p. 52) Cite error: The named reference "Regular52" was defined multiple times with different content (see the help page).
  14. ^ Denyer (1992, p. 72)
  15. Mead (2002, pp. 28 and 81)
  16. Duckworth (2007, p. 339)
  17. Griewank (2010, p. 10)
  18. ^ Denyer (1992, p. 121)
  19. ^ Denyer (1992, p. 119)
  20. Griewank (2010, pp. 9–10)
  21. Denyer (1992, p. 105)
  22. Denyer (1992, pp. 74–75)
  23. Zemb, Patrick (2007). "Sommaire du site musical (French: Summary of the musical site)". English machine-translation. Retrieved 29 August 2012. {{cite web}}: Check date values in: |accessdate= (help); Invalid |ref=harv (help); Unknown parameter |month= ignored (help)
  24. ^ White (2005)
  25. Griewank (2010, p. 5)
  26. Griewank (2010, p. 13, with listing on pp. 20–21)
  27. Sethares (2001, "The major third tuning" (pp. 56–57), listing on p. 57)
  28. ^ Sethares (2001, p. 53)
  29. Duckworth (2007, pp. 128–129)
  30. ^ Smith (1980, pp. +guitar&source=bl&ots=seCZQAD7RX&sig=nhqO8E351RuaTrQpf7ugGXouBBk&hl=sv&sa=X&ei=ZKFsUMm6A62L4gTx6oE4&ved=0CEcQ6AEwBQ#v=onepage&q=dropped%20dominant%20seventh%20chord%2C%20guitar&f=false 92–93)
  31. Kolb (2005, p. 37)
  32. Fisher (2002, pp. +guitar&source=bl&ots=NO2aVmwcD1&sig=yNYMGtuB88mb-8b80Z6dd0lhyPM&hl=sv&sa=X&ei=yaFsUIycEaj14QTr94D4BA&ved=0CDgQ6AEwAjgK#v=onepage&q=dropped%20dominant%20seventh%20chord%2C%20guitar&f=false 30–33)
  33. Patt (2008)
  34. Sethares (2012)

Bibliography

Further reading

  • Sethares, Bill (2009) . Alternate tuning guide (pdf). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. Retrieved 19 May 2012. {{cite book}}: Check date values in: |accessdate= (help); Invalid |ref=harv (help); Unknown parameter |month= ignored (help)

External links


Guitar tunings
General
Open (Slide and slack-key guitar)
TuningRepetitiveOvertonesOther
(often most popular)
  • A-C♯-E-A-C♯-E
  • B-D♯-F♯-B-D♯-F♯
  • C-E-G-C-E-G
  • D-F♯-A-D-F♯-A
  • E-G♯-B-E-G♯-B
  • F-A-C-F-A-C
  • G-B-D-G-B-D
Regular (semitones)
Repetitive (open pitches)
Miscellaneous
Categories: