Misplaced Pages

This is an old revision of this page, as edited by Ruud Koot (talk | contribs) at 13:09, 30 July 2013. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

In the history of mathematics, mathematics in medieval Islam, often called Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and advanced under the Islamic civilization between circa 622 and c.1600. Islamic science and mathematics flourished under the Islamic caliphate established across the Middle East, extending from the Iberian Peninsula in the west to the Indus in the east and to the Almoravid Dynasty and Mali Empire in the south.

In his A History of Mathematics, Victor Katz says that:

A complete history of mathematics of medieval Islam cannot yet be written, since so many of these Arabic manuscripts lie unstudied... Still, the general outline... is known. In particular, Islamic mathematicians fully developed the decimal place-value number system to include decimal fractions, systematised the study of algebra and began to consider the relationship between algebra and geometry, studied and made advances on the major Greek geometrical treatises of Euclid, Archimedes, and Apollonius, and made significant improvements in plane and spherical geometry.

An important role was played by the translation and study of Greek mathematics, which was the principal route of transmission of these texts to Western Europe. Smith notes that:

The world owes a great debt to Arab scholars for preserving and transmitting to posterity the classics of Greek mathematics... their work was chiefly that of transmission, although they developed considerable ingenuity in algebra and showed some genius in their work in trigonometry.

Adolph P. Yushkevich states regarding the role of Islamic mathematics:

The Islamic mathematicians exercised a prolific influence on the development of science in Europe, enriched as much by their own discoveries as those they had inherited by the Greeks, the Indians, the Syrians, the Babylonians, etc.

History

The most important contribution of the Islamic mathematicians was the development of algebra; combining Indian and Babylonian material with the Greek geometry to develop algebra. In Algebra a mathematician substitutes symbols such as x, y or z for numbers in order to solve mathematical problems.

Irrational numbers

The Greeks had discovered Irrational numbers, but were not happy with them and only able to cope by drawing a distinction between magnitude and number. In the Greek view, magnitudes varied continuously and could be used for entities such as line segments, whereas numbers were discrete. Hence, irrationals could only be handled geometrically; and indeed Greek mathematics was mainly geometrical. Islamic mathematicians including Abū Kāmil Shujāʿ ibn Aslam slowly removed the distinction between magnitude and number, allowing irrational quantities to appear as coefficients in equations and to be solutions of algebraic equations. They worked freely with irrationals as objects, but they did not examine closely their nature.

In the twelfth century, Latin translations of Al-Khwarizmi's Arithmetic on the Indian numerals introduced the decimal positional number system to the Western world. His Compendious Book on Calculation by Completion and Balancing presented the first systematic solution of linear and quadratic equations. In Renaissance Europe, he was considered the original inventor of algebra, although it is now known that his work is based on older Indian or Greek sources. He revised Ptolemy's Geography and wrote on astronomy and astrology.

Induction

The earliest implicit traces of mathematical induction can be found in Euclid's proof that the number of primes is infinite (c. 300 BCE). The first explicit formulation of the principle of induction was given by Pascal in his Traité du triangle arithmétique (1665).

In between, implicit proof by induction for arithmetic sequences was introduced by al-Karaji (c. 1000) and continued by al-Samaw'al, who used it for special cases of the binomial theorem and properties of Pascal's triangle.

Major figures and developments

Omar Khayyám

Omar Khayyám (c. 1038/48 in Iran – 1123/24) wrote the Treatise on Demonstration of Problems of Algebra containing the systematic solution of third-degree equations, going beyond the Algebra of Khwārazmī. Khayyám obtained the solutions of these equations by finding the intersection points of two conic sections. This method had been used by the Greeks, but they did not generalize the method to cover all equations with positive roots.

Sharaf al-Dīn al-Ṭūsī

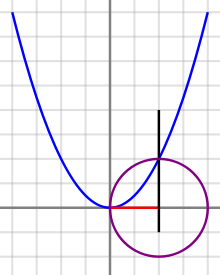
Sharaf al-Dīn al-Ṭūsī (? in Tus, Iran – 1213/4) developed a novel approach to the investigation of cubic equations—an approach which entailed finding the point at which a cubic polynomial obtains its maximum value. For example, to solve the equation ${\displaystyle \ x^{3}+a=bx}$, with a and b positive, he would note that the maximum point of the curve ${\displaystyle \ y=bx-x^{3}}$ occurs at ${\displaystyle x=\textstyle {\sqrt {\frac {b}{3}}}}$, and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than a. His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.

Other major figures

• 'Abd al-Hamīd ibn Turk (fl. 830) (quadratics)
• Thabit ibn Qurra (826–901)
• Abū Kāmil Shujā ibn Aslam (c. 850 – 930) (irrationals)
• Sind ibn Ali
• Abū Sahl al-Qūhī (c. 940–1000) (centers of gravity)
• Abu'l-Hasan al-Uqlidisi (952 – 953) (arithmetic)
• 'Abd al-'Aziz al-Qabisi
• Abū al-Wafā' Būzjānī (940 – 998) (spherical trigonometry)
• Al-Karaji (c. 953 – c. 1029) (algebra, induction)
• Abu Nasr Mansur (c. 960 – 1036) (spherical trigonometry)
• Ibn Tahir al-Baghdadi (c. 980–1037) (irrationals)
• Ibn al-Haytham (ca. 965–1040)
• Abū al-Rayḥān al-Bīrūnī (973 – 1048) (trigonometry)
• Omar Khayyam (1048–1131) (cubic equations, parallel postulate)
• Ibn Yaḥyā al-Maghribī al-Samawʾal (c. 1130 – c. 1180)
• Ibn Maḍāʾ (c. 1116 - 1196)
• Sharaf al-Dīn al-Ṭūsī (c. 1150–1215) (cubics)
• Naṣīr al-Dīn al-Ṭūsī (1201–1274) (parallel postulate)
• Jamshīd al-Kāshī (c. 1380–1429) (decimals and estimation of the circle constant)

See also

• Timeline of Islamic science and technology
• Islamic Golden Age
• Hindu and Buddhist contribution to science in medieval Islam
• History of geometry

Notes

1. Hogendijk 1999.
2. Katz 1993.
3. Smith 1958, Vol. 1, Chapter VII.4.
4. Sertima, Ivan Van (1992), Golden age of the Moor, Volume 11, Transaction Publishers, p. 394, ISBN 1-56000-581-5
5. O'Connor, John J.; Robertson, Edmund F., "Al-Biruni", MacTutor History of Mathematics Archive, University of St Andrews
6. Douglas, A. V. (1973), "R.A.S.C. Papers- Al-Biruni, Persian Scholar", Journal of the Royal Astronomical Society of Canada, 67: 973–1048, Bibcode:1973JRASC..67..209D
7. http://www.math.tamu.edu/~dallen/history/infinity.pdf
8. Struik 1987, p. 93
9. Rosen 1831, p. v–vi harvnb error: no target: CITEREFRosen1831 (help); Toomer 1990 harvnb error: no target: CITEREFToomer1990 (help)
10. Struik 1987, p. 96.
11. Boyer 1991, pp. 241–242.
12. Struik 1987, p. 97.
13. Boyer & 19991, pp. 241–242. sfn error: no target: CITEREFBoyer19991 (help)
14. Berggren, J. Lennart; Al-Tūsī, Sharaf Al-Dīn; Rashed, Roshdi; Al-Tusi, Sharaf Al-Din (1990), "Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī's al-Muʿādalāt", Journal of the American Oriental Society, 110 (2): 304–309, doi:10.2307/604533, JSTOR 604533

References

• Boyer, Carl B. (1991), "Greek Trigonometry and Mensuration, and The Arabic Hegemony", A History of Mathematics (2nd ed.), New York City: John Wiley & Sons, ISBN 0-471-54397-7 {{citation}}: Invalid |ref=harv (help)
• Katz, Victor J. (1993), A History of Mathematics: An Introduction, HarperCollins college publishers, ISBN 0-673-38039-4 {{citation}}: Invalid |ref=harv (help).
• Ronan, Colin A. (1983), The Cambridge Illustrated History of the World's Science, Cambridge University Press, ISBN 0-521-25844-8 {{citation}}: Invalid |ref=harv (help)
• Smith, David E. (1958), History of Mathematics, Dover Publications, ISBN 0-486-20429-4 {{citation}}: Invalid |ref=harv (help)
• Struik, Dirk J. (1987), A Concise History of Mathematics (4th rev. ed.), Dover Publications, ISBN 0-486-60255-9 {{citation}}: Invalid |ref=harv (help)

Further reading

Books on Islamic mathematics

• Berggren, J. Lennart (1986), Episodes in the Mathematics of Medieval Islam, New York: Springer-Verlag, ISBN 0-387-96318-9
  • Review: Toomer, Gerald J.; Berggren, J. L. (1988), "Episodes in the Mathematics of Medieval Islam", American Mathematical Monthly, 95 (6), Mathematical Association of America: 567, doi:10.2307/2322777, JSTOR 2322777
  • Review: Hogendijk, Jan P.; Berggren, J. L. (1989), "Episodes in the Mathematics of Medieval Islam by J. Lennart Berggren", Journal of the American Oriental Society, 109 (4), American Oriental Society: 697–698, doi:10.2307/604119, JSTOR 604119)
• Daffa', Ali Abdullah al- (1977), The Muslim contribution to mathematics, London: Croom Helm, ISBN 0-85664-464-1
• Rashed, Roshdi (2001), The Development of Arabic Mathematics: Between Arithmetic and Algebra, Transl. by A. F. W. Armstrong, Springer, ISBN 0-7923-2565-6
• Youschkevitch, Adolf P. (1960), Die Mathematik der Länder des Ostens im Mittelalter, Berlin {{citation}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)CS1 maint: location missing publisher (link) Sowjetische Beiträge zur Geschichte der Naturwissenschaft pp. 62–160.
• Youschkevitch, Adolf P. (1976), Les mathématiques arabes: VIII–XV siècles, translated by M. Cazenave and K. Jaouiche, Paris: Vrin, ISBN 978-2-7116-0734-1

Book chapters on Islamic mathematics

• Berggren, J. Lennart (2007), "Mathematics in Medieval Islam", in Victor J. Katz (ed.), The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (Second ed.), Princeton, New Jersey: Princeton University, ISBN 978-0-691-11485-9{{citation}}: CS1 maint: ref duplicates default (link)
• Cooke, Roger (1997), "Islamic Mathematics", The History of Mathematics: A Brief Course, Wiley-Interscience, ISBN 0-471-18082-3

Books on Islamic science

• Daffa, Ali Abdullah al-; Stroyls, J.J. (1984), Studies in the exact sciences in medieval Islam, New York: Wiley, ISBN 0-471-90320-5
• Kennedy, E. S. (1984), Studies in the Islamic Exact Sciences, Syracuse Univ Press, ISBN 0-8156-6067-7

Books on the history of mathematics

• Joseph, George Gheverghese (2000), The Crest of the Peacock: Non-European Roots of Mathematics (2nd ed.), Princeton University Press, ISBN 0-691-00659-8 (Reviewed: Katz, Victor J.; Joseph, George Gheverghese (1992), "The Crest of the Peacock: Non-European Roots of Mathematics by George Gheverghese Joseph", The College Mathematics Journal, 23 (1), Mathematical Association of America: 82–84, doi:10.2307/2686206, JSTOR 2686206)
• Youschkevitch, Adolf P. (1964), Gesichte der Mathematik im Mittelalter, Leipzig: BG Teubner Verlagsgesellschaft

Journal articles on Islamic mathematics

• Høyrup, Jens. “The Formation of «Islamic Mathematics»: Sources and Conditions”. Filosofi og Videnskabsteori på Roskilde Universitetscenter. 3. Række: Preprints og Reprints 1987 Nr. 1.

Bibliographies and biographies

• Brockelmann, Carl. Geschichte der Arabischen Litteratur. 1.–2. Band, 1.–3. Supplementband. Berlin: Emil Fischer, 1898, 1902; Leiden: Brill, 1937, 1938, 1942.
• Sánchez Pérez, José A. (1921), Biografías de Matemáticos Árabes que florecieron en España, Madrid: Estanislao Maestre
• Sezgin, Fuat (1997), Geschichte Des Arabischen Schrifttums (in German), Brill Academic Publishers, ISBN 90-04-02007-1
• Suter, Heinrich (1900), Die Mathematiker und Astronomen der Araber und ihre Werke, Abhandlungen zur Geschichte der Mathematischen Wissenschaften Mit Einschluss Ihrer Anwendungen, X Heft, Leipzig{{citation}}: CS1 maint: location missing publisher (link)

Television documentaries

• Marcus du Sautoy (presenter) (2008). "The Genius of the East". The Story of Maths. BBC.
• Jim Al-Khalili (presenter) (2010). Science and Islam. BBC.

External links

• Hogendijk, Jan P. (January 1999). "Bibliography of Mathematics in Medieval Islamic Civilization". {{cite web}}: Invalid |ref=harv (help)CS1 maint: date and year (link)
• O'Connor, John J.; Robertson, Edmund F. (1999), "Arabic mathematics: forgotten brilliance?", MacTutor History of Mathematics Archive, University of St Andrews
• Richard Covington, Rediscovering Arabic Science, 2007, Saudi Aramco World

v t e Mathematics in the medieval Islamic world
Mathematicians	9th century 'Abd al-Hamīd ibn Turk Sanad ibn Ali al-Jawharī Al-Ḥajjāj ibn Yūsuf Al-Kindi Qusta ibn Luqa Al-Mahani al-Dinawari Banū Mūsā brothers Hunayn ibn Ishaq Al-Khwarizmi Yusuf al-Khuri Ishaq ibn Hunayn Na'im ibn Musa Thābit ibn Qurra al-Marwazi Abu Said Gorgani 10th century Abu al-Wafa al-Khazin Al-Qabisi Abu Kamil Ahmad ibn Yusuf Aṣ-Ṣaidanānī Sinān ibn al-Fatḥ al-Khojandi Al-Nayrizi Al-Saghani Brethren of Purity Ibn Sahl Ibn Yunus al-Uqlidisi Al-Battani Sinan ibn Thabit Ibrahim ibn Sinan Al-Isfahani Nazif ibn Yumn al-Qūhī Abu al-Jud Al-Sijzi Al-Karaji al-Majriti al-Jabali 11th century Abu Nasr Mansur Alhazen Kushyar Gilani Al-Biruni Ibn al-Samh Abu Mansur al-Baghdadi Avicenna al-Jayyānī al-Nasawī al-Zarqālī ibn Hud Al-Isfizari Omar Khayyam Muhammad al-Baghdadi 12th century Jabir ibn Aflah Al-Kharaqī Al-Khazini Al-Samawal al-Maghribi al-Hassar Sharaf al-Din al-Tusi Ibn al-Yasamin 13th century Ibn al‐Ha'im al‐Ishbili Ahmad al-Buni Ibn Munim Alam al-Din al-Hanafi Ibn Adlan al-Urdi Nasir al-Din al-Tusi al-Abhari Muhyi al-Din al-Maghribi al-Hasan al-Marrakushi Qutb al-Din al-Shirazi Shams al-Din al-Samarqandi Ibn al-Banna' Kamāl al-Dīn al-Fārisī 14th century Nizam al-Din al-Nisapuri Ibn al-Shatir Ibn al-Durayhim Al-Khalili al-Umawi 15th century Ibn al-Majdi al-Rūmī al-Kāshī Ulugh Beg Ali Qushji al-Wafa'i al-Qalaṣādī Sibt al-Maridini Ibn Ghazi al-Miknasi 16th century Al-Birjandi Muhammad Baqir Yazdi Taqi ad-Din Ibn Hamza al-Maghribi
Mathematical works	The Compendious Book on Calculation by Completion and Balancing De Gradibus Principles of Hindu Reckoning Book of Optics The Book of Healing Book on the Measurement of Plane and Spherical Figures Encyclopedia of the Brethren of Purity Toledan Tables Tabula Rogeriana Zij
Concepts	Alhazen's problem Islamic geometric patterns
Centers	Al-Azhar University Al-Mustansiriya University House of Knowledge House of Wisdom Constantinople observatory of Taqi ad-Din Madrasa Maragheh observatory University of al-Qarawiyyin
Influences	Babylonian mathematics Greek mathematics Indian mathematics
Influenced	Byzantine mathematics European mathematics Indian mathematics
Related	Hindu–Arabic numeral system Arabic numerals (Eastern Arabic numerals, Western Arabic numerals) Trigonometric functions History of trigonometry History of algebra

• Islamic mathematics
• Islamic Golden Age