Misplaced Pages

This is an old revision of this page, as edited by Anonymous 57 (talk | contribs) at 20:54, 3 October 2006 (→Record free fall: requesting citations, rephrasing). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Free fall in its strictest sense is the condition of acceleration which is due only to gravity. In other words, the objects undergoing free fall experience only one force: their own weight.

Examples include:

• a spacecraft with its rockets off
• the Moon's trajectory around the Earth, the Earth's orbit around the Sun, or an asteroid's orbit around the Sun.
• on Earth, falling through a vacuum tube or shaft, e.g.:
  • for a physics demonstration
  • at NASA's Zero-G Research Facility

as opposed to the cases where other forces are acting, including:

• standing on the ground, sitting in a chair on the ground, etc. (gravity is cancelled by the reaction force of the ground)
• flying in a plane (gravity is cancelled by the lift the wings provide) - see below for special trajectories which form an exception
• atmospheric reentry, landing on a parachute: gravity is opposed by atmospheric drag
• during an orbital maneuver in a spacecraft: the rocket provides thrust

More generally, free fall is the condition of acceleration due to gravity and air friction: in parachuting, free fall (skydiving) refers to the act of falling and delaying the opening of a parachute. Freeflying is skydiving in other body positions than the more standard belly flying.

With air friction acting upon an object that has been dropped the object will eventually reach terminal velocity (around 120 miles/hour for a human body flying in the belly-down arched position; terminal velocity depends on many factors including mass, drag coefficient, and relative surface area) if the fall is from sufficient altitude (2,000 ft) and also otherwise uninterrupted.

Free-fall under a constant gravity

Without air drag

${\displaystyle v_{y}=-gt+v_{y0}\,}$

${\displaystyle y=-{\frac {1}{2}}gt^{2}+v_{y0}t+y_{0}}$

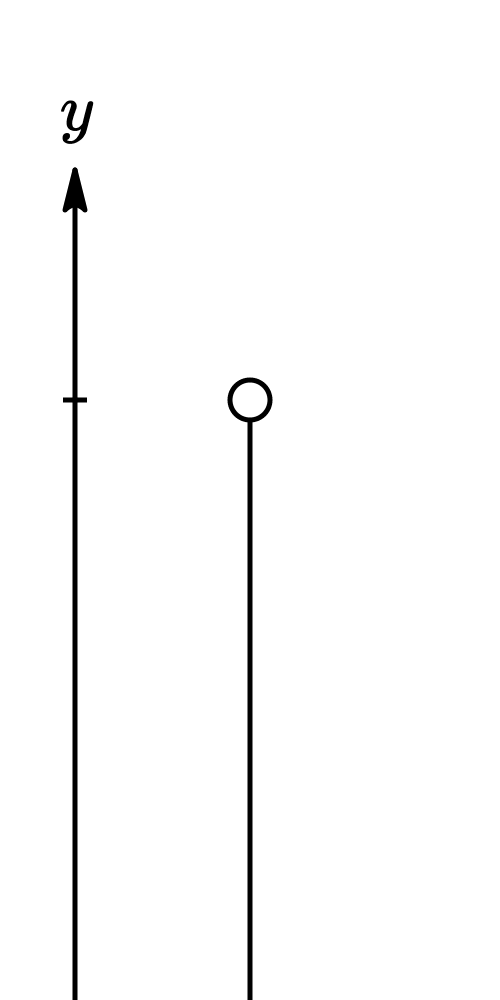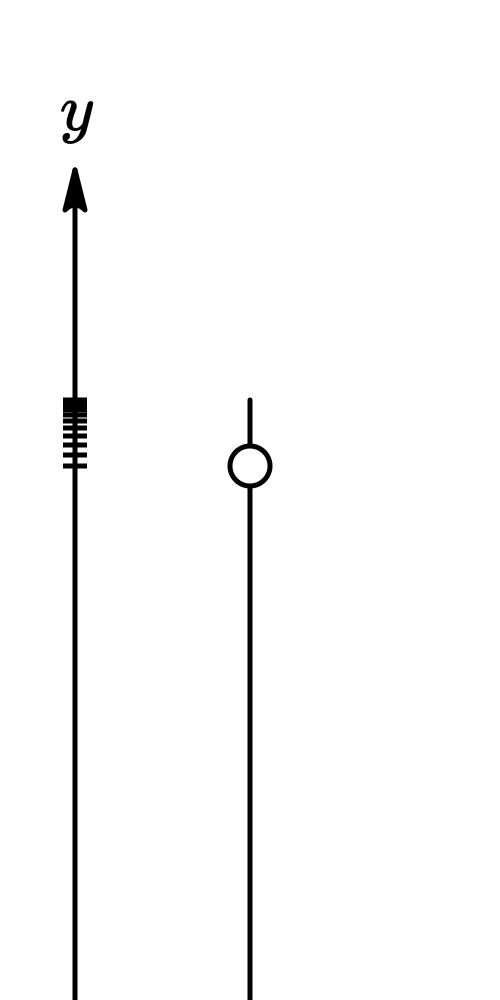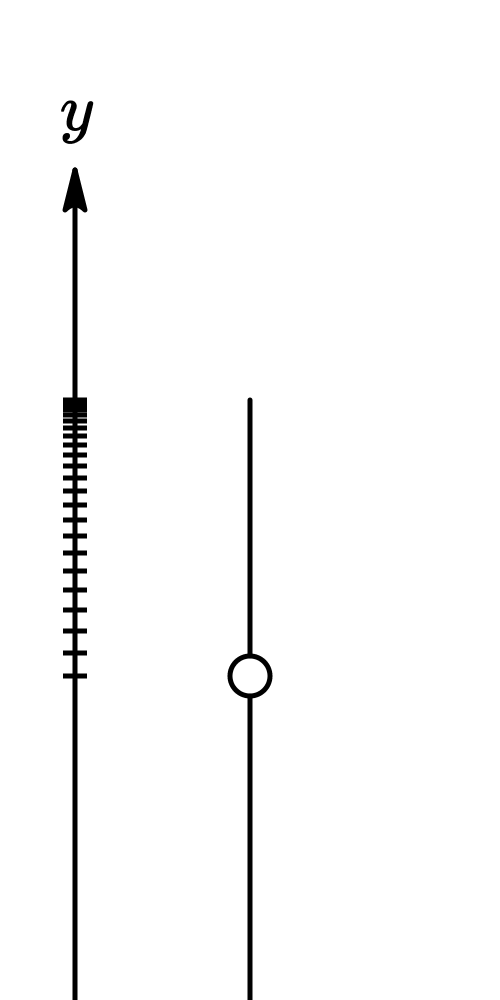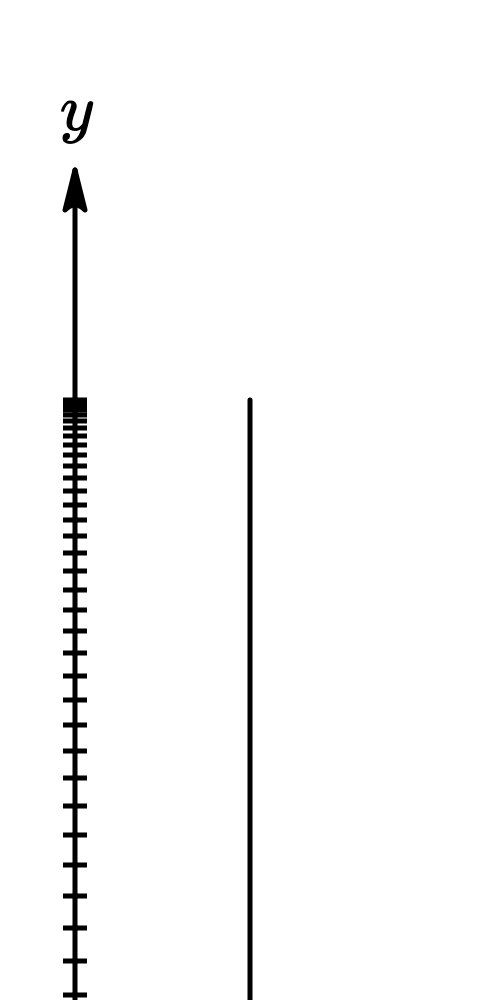
where

${\displaystyle v_{y0}}$ is the initial velocity

${\displaystyle y_{0}}$ is the initial altitude

${\displaystyle t}$ is time

${\displaystyle g}$ is acceleration due to gravity

With air drag

${\displaystyle {\dot {v}}=-kv+mg}$

${\displaystyle v_{y}=(v_{y0}+{\frac {m}{k}}g)e^{-kt})-{\frac {m}{k}}g}$

${\displaystyle y=-{\frac {m}{k}}\{(v_{yo}+{\frac {m}{k}}g)(e^{-kt}-1)+gt\}+y_{0}}$

${\displaystyle v_{y\infty }=\lim _{t\to \infty }v_{y}=-{\frac {m}{k}}g}$

where

${\displaystyle m}$ is mass of the object

${\displaystyle k}$ is the air drag coefficient

${\displaystyle v_{y\infty }}$ is the terminal velocity

Free Fall Simulators

There are various simulators. You can set a simulator in a spreadsheet or other software package for small distances using the equations above. When the altitude is more than a few hundred feet, the conditions will change. Here is a list of online calculators that can simulate freefall.

eXtreme High Altitude Calculator - models air pressure, temperature, gravity and even coeffients of drag. Good to any altitude including space.

People surviving free fall

At least three airmen survived free falls of around 20,000 ft (6,000 m) without a parachute in the Second World War; Lt. I.M. Chisov was a Russian bomber pilot, Sgt. Alan Magee was an American gunner on a B-17, and Sgt. Nicholas Alkemade was a British gunner on a Lancaster bomber. It is estimated that a person free falling in the "box" position reaches a terminal velocity of around 120 mph (200 km/h) after a fall of just 1,000 ft (300 m), so the additional 19,000 ft (5,700 m) doesn't make these falls that much more dangerous, apart from the lack of oxygen at high altitude. All three men lost consciousness during their falls, and two of them landed on terrain covered in deep snow, which was probably a significant factor in the survivability of the falls.

Vesna Vulović, a flight attendant from Yugoslavia, survived a fall from 10,160 m (33,330 ft) when the DC-9 airplane she was traveling in blew up over Srbská Kamenice, Czechoslovakia, on January 26, 1972. She remained strapped into her flight attendant's seat in the tail section of the plane, which remained attached to the washrooms. The assembly struck the snow-covered flank of a mountain. A terrorist bomb was thought to be the cause. Vulović broke both legs and was temporarily paralyzed from the waist down. No other passengers survived.

Stories about Russians deploying paratroopers without parachutes (unsuccessfully) during World War II are most likely fabricated.

It was reported that two of the victims of the Lockerbie bombing survived for a brief period after hitting the ground.

Record free fall

As part of Project Excelsior on 16 August 1960, Joseph Kittinger achieved the record for the longest free fall jump and the fastest maximum speed of 614 mph (982 km/h), before opening his parachute at around 18,000 feet (5,500 m). Kittinger started the jump from a specially constructed balloon at an altitude of 102,800 feet (31,300 m), which also qualified him for the highest balloon ascent and highest parachute jump.

Some contend that Kittinger's jump wasn't true free-fall as he used a drogue chute for stability. According to the Guinness book of records, Eugene Andreev (USSR) holds the official FAI record for the longest free-fall parachute jump after falling for 80,380 ft (24,500 m) from an altitude of 83,523 ft (25,457 m) near the city of Saratov, Russia on November 1, 1962. Andreev did not use a drogue chute during his jump.

External link

• Unplanned Freefall? A slightly tongue-in-cheek look at surviving free-fall without a parachute.

References

• Free fall accidents, mathematics of free fall - detailed research on the topic
• Free fall accidents and parachute history

1. Cox, Matthew, and Foster, Tom. (1992) Their Darkest Day: The Tragedy of Pan Am 103, ISBN 0-8021-1382-6

• Gravity
• Parachuting
• Introductory physics