Misplaced Pages

This is an old revision of this page, as edited by Borisblue (talk | contribs) at 15:02, 7 October 2006 (→See also: this should be enough). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Leonhard Euler
Portrait of Leonhard Euler by Johann Georg Brucker.
Born	April 15, 1707 Basel, Switzerland
Died	September 18, 1783 St Petersburg, Russia
Nationality	Swiss
Alma mater	University of Basel
Known for	Analysis, number theory, graph theory
Scientific career
Fields	Mathematics
Institutions	Imperial Russian Academy of Sciences, Berlin Academy

Leonhard Euler (pronounced , that is, Oiler) (Basel, Switzerland, April 15, 1707 – St Petersburg, Russia, September 18, 1783) was a Swiss mathematician and physicist. He developed important concepts and established mathematical theorems in fields as diverse as calculus, number theory and topology. He introduced the fundamental notion of a mathematical function, and set much of the modern mathematical terminology: his two-volume Introductio in analysin infinitorum (1748) established a lot of the notation for analysis. He is also renowned for his work in mechanics, optics and astronomy.

Euler is considered to be the preeminent mathematician of the 18th century and one of the greatest of all time; he is also listed on the Guinness Book of Records as the most prolific, with collected works filling between 60 and 80 quarto volumes. Euler was featured on the Swiss 10-franc banknote as well as numerous Swiss, German and Russian stamps and had an asteroid (2002 Euler) named in his honor.

The measure of his influence can be expressed by this quote often attributed to Pierre-Simon Laplace: "Lisez Euler, lisez Euler, c'est notre maître à tous." (Read Euler, read Euler, he is a master for us all).

Biography

Childhood

Euler’s parents were Paul Euler, a pastor of the Reformed Church, and Marguerite Brucker, a pastor's daughter. He had two younger sisters named Anna Maria and Maria Magdalena. Soon after the birth of Leonhard, the Eulers moved from Basel to the town of Riehen, where Euler spent most of his childhood. Paul Euler was a family friend of the Bernoullis, and Johann Bernoulli, who was then regarded as Europe's foremost mathematician, would eventually be an important influence on the young Leonhard. His early formal education started in Basel, where he was sent to live with his maternal grandmother. At the age of thirteen he matriculated at the University of Basel, and in 1723, received a masters of philosophy degree with a dissertation that compared the philosophies of Descartes and Newton. At this time, he was receiving Saturday afternoon lessons from Johann Bernoulli who quickly discovered his new pupil's incredible talent for mathematics.

Euler was at this point studying Theology, Greek and Hebrew at his father's urging, in order to become a pastor. Johann Bernoulli intervened, and convinced Paul Euler that Leonhard was destined to become a great mathematician. In 1726, Euler completed his Ph.D. dissertation on the propagation of sound and in 1727, he entered the Paris Academy Prize Problem competition, where the problem that year was to find the best way to place the masts on a ship. He won second place, losing only to Pierre Bouguer—a man now known as "the father of naval architecture". Euler, however, would eventually win the coveted annual prize twelve times in his career.

St. Petersburg

Around this time Johann Bernoulli's two sons, Daniel and Nicolas were working at the Imperial Russian Academy of Sciences in St Petersburg. In July 1726, Nicolas died of appendicitis after spending a year in Russia, and when Daniel assumed his brother's position in the mathematics/physics division he recommended that the post in physiology that he vacated be filled by his friend Euler. In November 1726 Euler eagerly accepted the offer, but delayed making the trip to St Petersburg. In the interim he unsuccessfully applied for a physics professorship at the University of Basel.

Euler arrived in the Russian capital on May 17, 1727. He was promoted from his junior post in the medical department of the academy to a position in the mathematics department. He lodged with Daniel Bernoulli with whom he often worked in close collaboration. Euler mastered Russian and settled into life in St Petersburg, even briefly taking on an additional job as a medic in the Russian Navy.

The Academy at St. Petersburg, established by Peter the Great, was intended to improve education in Russia and to close the scientific gap with Western Europe. As a result, it was made especially attractive to foreign scholars like Euler: the academy possessed ample financial resources and a comprehensive library drawn from the private libraries of Peter himself and of the nobility. Very few students were enrolled in the academy so as to lessen the faculty's teaching burden, and the academy emphasized research and offered to its faculty both the time and the freedom to pursue scientific questions.

However, the Academy's benefactress, Catherine I, who had attempted to continue the progressive policies of her late husband, died shortly before Euler's arrival. The Russian nobility then gained power upon the ascension of the twelve-year-old Peter II. The nobility were suspicious of the academy's foreign scientists, and thus cut funding and caused numerous other difficulties for the faculty.

Conditions improved slightly upon the death of Peter II, and Euler swiftly rose through the ranks in the academy and was made professor of physics in 1731. Two years later, Daniel Bernoulli, who was fed up with the censorship and hostility he faced at St. Petersburg, left for Basel. Euler succeeded him as the head of the mathematics department.

On January 7, 1734, he married Katharina Gsell, daughter of a painter from the Academy Gymnasium. The young couple bought a house by the River Neva, and had thirteen children, of whom only five survived childhood.

Berlin

Concerned about continuing turmoil in Russia, Euler debated whether to stay in St. Petersburg or not. Frederick the Great of Prussia offered him a post at the Berlin Academy, which he accepted. He left St. Petersburg on June 19, 1741 and lived twenty-five years in Berlin, where he wrote over 380 articles. In Berlin, he published the two works which he would be most renowned for: the Introductio in analysin infinitorum, a text on functions published in 1748 and the Institutiones calculi differntialis, a work on differential calculus.

In addition, Euler was asked to tutor the Princess of Anhalt-Dessau, Frederick's niece. He wrote over 200 letters to her, which were later compiled into a best-selling volume, titled the Letters of Euler on different Subjects in Natural Philosophy Addressed to a German Princess. This work contained Euler's exposition on various subjects pertaining to physics and mathematics, as well as offering valuable insight on Euler's personality and religious beliefs. This book ended up being more widely read than any of his mathematical works, and was published all across Europe and in the United States. The popularity of the Letters testifies to Euler's ability to communicate scientific matters effectively to a lay audience, a rare ability for a dedicated research scientist.

Despite Euler's immense contribution to the Academy's prestige, he was soon forced to leave Berlin. This was caused in part by a personality conflict with Frederick. Frederick came to regard him as unsophisticated especially in comparison to the circle of philosophers the German king brought to the Academy. Voltaire was among those in Frederick's employ, and the Frenchman enjoyed a favored position in the king's social circle. Euler, a devout religious man and a hard worker, was in many ways the direct opposite of Voltaire. Euler had very limited training in philosophy and tended to debate matters that he knew little about, making him a frequent target of Voltaire's wit.

Eyesight deterioration

Euler's eyesight worsened throughout his mathematical career. Three years after suffereing a near-fatal fever in 1735 he became nearly blind in his right eye, but Euler rather blamed his condition on the painstaking work on cartography he performed for the St. Petersburg Academy. Euler's sight in that eye worsened throughout his stay in Germany, so much so that Frederick referred to him as "Cyclops". Euler later suffered a cataract in his good left eye, rendering him almost totally blind. Even so, his condition appeared to have little effect on his productivity, as he compensated for it with his mental calculation skills and photographic memory. For example, Euler could repeat the Aeneid of Virgil from beginning to end without hestitation, and indicate the first and last line of every page in the edition he used.

Return to Russia

The situation in Russia had improved greatly since the ascension of Catherine the Great, and in 1766 Euler accepted an invitation to return to the St. Petersburg Academy and spent the rest of his life in Russia. His second stay in the country was marred by tragedy. A 1771 fire in St. Petersburg cost him his home and almost his life and, in 1773, he lost his wife of 40 years. Euler would eventually remarry three years later.

On September 18, 1783, Euler passed away after suffering a brain hemorrhage and was buried in the Alexander Nevsky Monastery. His eulogy was written for the French Academy by the French mathematician and philosopher Marquis de Condorcet, and an account of his life, with a list of his works, by Nikolaus von Fuss, Euler's son-in-law and the secretary of the Imperial Academy of St. Petersburg. Condorcet commented,

"...il cessa de calculer et de vivre," (he ceased to calculate and to live).

Contributions to mathematics

Euler worked in almost all areas of mathematics: geometry, calculus, trigonometry, algebra, and number theory, not to mention continuum physics, lunar theory and other areas of physics. His importance in the history of mathematics cannot be overstated: if printed, his works, many of which are of fundamental interest, would occupy between 60 and 80 quarto volumes and Euler's name is associated with an impressive number of topics. The 20th century Hungarian mathematician Paul Erdös is perhaps the only mathematician that can claim to have been as prolific.

Mathematical notation

Euler introduced and popularized several notational conventions through his numerous and widely circulated textbooks. Most notably, he was the first to write f(x) to denote the function f applied to the argument x. He also introduced the modern notation for the trigonometric functions, the use the letter e for the base of the natural logarithm (now also known as Euler's number), the use of the Greek letter ${\displaystyle \Sigma }$ to indicate summations and the use of i to denote ${\displaystyle {\sqrt {-1}}}$. The use of the Greek letter π to denote the ratio of a circle's circumference to its diameter was also popularized (though not invented) by Euler.

Complex analysis

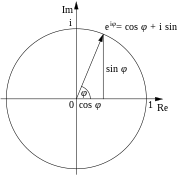
Euler made important contributions to complex analysis. He discovered what is now known as Euler's formula: for any real number Φ, the complex exponential function satisfies

${\displaystyle e^{i\phi }=\cos \phi +i\sin \phi \!.}$

A special case of the above formula is known as Euler's identity:

${\displaystyle e^{i\pi }+1=0\,.}$

The identity has been called "the most remarkable formula in mathematics" by Richard Feynman. It is particularly dear to mathematicians as it involves e, π, i, 1 and 0, arguably the five most important constants in the field.

Analysis

The development of calculus was at the forefront of 18th century mathematical research, and the Bernoullis—family friends of Euler—were responsible for much of the early progress in the field. Understanding the infinite was naturally the major focus of Euler's research. While some of Euler's proofs may not have been acceptable under modern standards of rigor, his ideas were responsible for many great advances. First of all, Euler introduced the concept of a function, and introduced the use of the exponential function and logarithms in analytic proofs.

Euler frequently used the logarithm function as a tool in analysis problems, and discovered new ways by which they could be used. He discovered ways to express various logarithmic functions in terms of power series, and succesfully defined logarithms for complex and negative numbers, thus greatly expanding the scope where logarithms could be applied in mathematics.

Euler is well known in analysis for his frequent use and development of power series: that is, the expression of functions as sums of infinitely many terms, such as

${\displaystyle e=\sum _{n=0}^{\infty }{1 \over n!}=\lim _{n\to \infty }\left({\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+\cdots +{\frac {1}{n!}}\right)}$

Notably, Euler discovered the power series expansions for e and the inverse tangent function. His daring (and, by modern standards, technically incorrect) use of power series enabled him to solve the famous Basel problem in 1735:

${\displaystyle \lim _{n\to \infty }\left({\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}\right)={\frac {\pi ^{2}}{6}}}$

In addition, Euler elaborated the theory of higher transcendental functions by introducing the gamma function and introduced a new method for solving quartic equations. He also found a way to calculate integrals with complex limits, foreshadowing the development of complex analysis. Euler invented the calculus of variations including its most well-known result, the Euler-Lagrange equation.

Euler also pioneered the use of analytic methods to solve number theory problems. In doing so, he united two disparate branches of mathematics and introduced a new field of study, analytic number theory. In breaking ground for this new field, Euler created the theory of hypergeometric series, q-series, hyperbolic trigonometric functions and the analytic theory of continued fractions. For example, he proved the infinitude of primes using the divergence of the harmonic series, and used analytic methods to gain some understanding of the way prime numbers are distributed. Euler's work in this area led to the development of the prime number theorem.

Number theory

Euler's great interest in number theory can be traced to the influence of his friend in the St. Peterburg Academy, Christian Goldbach. A lot of his early work on number theory was based on the works of Pierre de Fermat, and developed some of Fermat's ideas while disproving some of his more outlandish conjectures.

One focus of Euler's work was to link the nature of prime distribution with ideas in analysis. He proved that the sum of the reciprocals of the primes diverges. In doing so, he discovered the connection between Riemann zeta function and prime numbers, known as the Euler product formula for the Riemann zeta function.

Euler proved Newton's identities, Fermat's little theorem, Fermat's theorem on sums of two squares, and made distinct contributions to Lagrange's four-square theorem. He also invented the totient function φ(n) which assigns to a positive integer n the number of positive integers less than n and coprime to n. Using properties of this function he was able to generalize Fermat's little theorem to what would become known as Euler's theorem. He further contributed significantly to the understanding of perfect numbers, which had fascinated mathematicians since Euclid. Euler made progress toward the prime number theorem and conjectured the law of quadratic reciprocity. The two concepts are regarded as the fundamental theorems of number theory, and his ideas paved the way for Carl Friedrich Gauss.

Graph theory

In 1736 Euler solved a problem known as the seven bridges of Königsberg. The city of Königsberg, Prussia (now Kaliningrad, Russia) is set on the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges. The question is whether it is possible to walk with a route that crosses each bridge exactly once, and return to the starting point. It is not. This solution is considered to be the first theorem of graph theory and planar graph theory while presaging the development of modern topology. Euler also introduced the notion now known as the Euler characteristic of a space and a formula relating the number of edges, vertices, and faces of a convex polyhedron with this constant. The study and generalization of this formula, specially by Cauchy and Lhuillier, is at the origin of topology.

Applied mathematics

Some of Euler's greatest successes were in using analytic methods to solve real world problems, describing numerous applications of Bernoulli's numbers, Fourier series, Venn diagrams, Euler numbers, e and π constants, continued fractions and integrals. He integrated Leibniz's differential calculus with Newton's method of fluxions, and developed tools that made it easier to apply calculus to physical problems. He made great strides in improving the numerical approximation of integrals, inventing what are now known as the Euler approximations. The most notable of these approximations are Euler's method and the Euler-Maclaurin formula. He also facilitated the use of differential equations, in particular introducing the Euler-Mascheroni constant:

${\displaystyle \gamma =\lim _{n\rightarrow \infty }\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots +{\frac {1}{n}}-\ln(n)\right).}$

One of Euler's more unusual interests was the application of mathematical ideas in music. In 1739 he wrote the Tentamen novae theoriae musicae, hoping to eventually integrate musical theory as part of mathematics. This part of his work, however, did not receive wide attention and was once described as too mathematical for musicians and too musical for mathematicians.

Physics and Astronomy

Aside from succesfully applying his analytic tools to problems in classical mechanics, Euler also applied these techniques to celestial problems. His work in astronomy was recognized by a number of Paris Academy Prizes over the course of his career. His accomplishments include determining with great accuracy the orbits of comets and other celestial bodies, understanding the nature of comets, and calculating the parallax of the sun. His calculations also contributed to the development of accurate longitude tables

In addition, Euler made important contributions in optics. He disagreed with Newton's corpuscular theory of light in the Opticks, which was then the prevailing theory. His 1740's papers on optics helped ensure that the wave theory of light proposed by Christian Huygens would become the dominant mode of thought until the development of the quantum theory of light.

Philosophy and religious beliefs

Euler and his friend Daniel Bernoulli were opponents of Leibniz's monadism and the philosophy of Christian Wolff. Euler insisted that knowledge is founded in part on the basis of precise quantitative laws, something that monadism and Wolffian science were unable to provide. Euler's religious leanings might also have had a bearing on his dislike of the doctrine, going so far as to label Wolff's ideas as "heathen and atheistic".

Much of what is known of Euler's religious beliefs can be deduced from his Letters to a German Princess and an earlier work, Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister (Defense of the Divine Revelation against the Objections of the Freethinkers). These works present Euler as a staunch Christian and a biblical literalist (for example, the Rettung was primarily an argument for the divine inspiration of scripture).

There is a famous anecdote inspired by Euler's arguments with secular philosophers over religion, which is set during Euler's second stint at the St. Petersburg academy. The French philosopher, Diderot, was visiting Russia on Catherine the Great's invitation. However, the Empress was alarmed that the philosopher's arguments for atheism were influencing members of her court, and so Euler was asked to confront the Frenchman. Diderot was later informed that a learned mathematician had produced a proof of the existence of God: he agreed to view the proof as it was presented in court. Euler appeared, advanced toward Diderot, and in a tone of perfect conviction announced, "Sir, ${\displaystyle {\begin{matrix}{\frac {a+b^{n}}{n}}=x\end{matrix}}}$, hence God exists—reply!". Diderot, to whom all mathematics were gibberish (or so the story says), stood dumbstruck as peals of laughter erupted from the court. Embarrassed, he asked to leave Russia, a request that was graciously granted by the Empress. However amusing the anecdote may be, it is almost certainly false, given that Diderot was actually a capable mathematician.

Selected bibliography

Euler has an extensive bibliography but his best known books include:

• Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti (1744). The latin title translates as a method for finding curved lines enjoying properties of maximum or minimum, or solution of isoperimetric problems in the broadest accepted sense.
• Introductio in analysin infinitorum (1748). English translation Introduction to Analysis of the Infinite by John Blanton (Book I, ISBN 0-387-96824-5, Springer-Verlag 1988; Book II, ISBN 0-387-97132-7, Springer-Verlag 1989).
• Two influential textbooks on calculus: Institutiones calculi differentialis (1755) and Institutiones calculi integralis (1768–1770).
• Lettres à une Princesse d'Allemagne (1768-1772); free book at http://www.bookmine.org;

See also

• List of topics named after Leonhard Euler

Notes

1. ^ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. p. 17.
2. ^ Boyer, Carl B. A History of Mathematics. John Wiley & Sons. pp. 439–445. ISBN 0471543977. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
3. "Guinness Book of Records: Most prolific mathematician". Retrieved September 2006. {{cite web}}: Check date values in: |accessdate= (help)
4. Edwards, Harold (1983). "Euler and Quadratic Reciprocity". Mathematics Magazine. 56 (5): 291. {{cite journal}}: Unknown parameter |month= ignored (help)
5. Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. pp. xiii.
6. James, Ioan (2002). Remarkable Mathematicians: From Euler to von Neumann. Cambridge. p. 2. ISBN 0-521-52094-0.
7. ^ Ronald Calinger (1996). "Leonhard Euler: The First St. Petersburg Years (1727-1741)". Historia Mathematica. 23 (2): 156. Cite error: The named reference "prize" was defined multiple times with different content (see the help page).
8. Ronald Calinger (1996). "Leonhard Euler: The First St. Petersburg Years (1727-1741)". Historia Mathematica. 23 (2): 125.
9. Ronald Calinger (1996). "Leonhard Euler: The First St. Petersburg Years (1727-1741)". Historia Mathematica. 23 (2): 127.
10. Ronald Calinger (1996). "Leonhard Euler: The First St. Petersburg Years (1727-1741)". Historia Mathematica. 23 (2): 128–129.
11. Fuss, Nicolas. "Eulogy of Euler by Fuss". {{cite web}}: Unknown parameter |accessmonthday= ignored (help); Unknown parameter |accessyear= ignored (|access-date= suggested) (help)
12. ^ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. pp. xxiv–xxv.
13. Ronald Calinger (1996). "Leonhard Euler: The First St. Petersburg Years (1727-1741)". Historia Mathematica. 23 (2): 154–155.
14. ^ Finkel, B.F. (1897). "Biography- Leonard Euler". The American Matehmatical Monthly. 4 (12): 300.
15. Marquis de Condorcet. "Eulogy of Euler - Condorcet". {{cite web}}: Unknown parameter |accessmonthday= ignored (help); Unknown parameter |accessyear= ignored (|access-date= suggested) (help)
16. Wolfram, Stephen. "Mathematical Notation: Past and Future". {{cite web}}: Unknown parameter |accessmonth= ignored (|access-date= suggested) (help); Unknown parameter |accessyear= ignored (|access-date= suggested) (help)
17. Feynman, Richard. "Chapter 22: Algebra". The Feynman Lectures on Physics: Volume I. pp. p.10. {{cite book}}: |pages= has extra text (help); Unknown parameter |origmonth= ignored (help)
18. Wanner, Gerhard (2005). Analysis by its history (1st ed.). Springer. p. 62. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help); Unknown parameter |month= ignored (help)
19. Dunham, William (1999). "3,4". Euler: The Master of Us All. The Mathematical Association of America.
20. Dunham, William (1999). "1,4". Euler: The Master of Us All. The Mathematical Association of America.
21. ^ Alexanderson, Gerald (2006). "Euler and Königsberg's bridges: a historical view" (PDF). Bulletin of the American Mathematical Society. {{cite journal}}: Unknown parameter |month= ignored (help)
22. Cauchy, A.L. (1813). "Recherche sur les polyèdres - premier mémoire". Journal de l'Ecole Polytechnique. 9 (Cahier 16): 66–86.
23. Lhuillier, S.-A.-J. (1861). "Mémoire sur la polyèdrométrie". Annales de Mathématiques. 3: 169–189.
24. Ronald Calinger (1996). "Leonhard Euler: The First St. Petersburg Years (1727-1741)". Historia Mathematica. 23 (2): 144–145.
25. A P Youschkevitch, Biography in Dictionary of Scientific Biography (New York 1970-1990).
26. R.W.Home (1988). "Leonhard Euler's 'Anti-Newtonian' Theory of Light". Annals of Science. 45 (5): 521–533.
27. Ronald Calinger (1996). "Leonhard Euler: The First St. Petersburg Years (1727-1741)". Historia Mathematica. 23 (2): 153–154.
28. Euler, Leonhard (1960). Orell-Fussli (ed.). "Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister". Leonhardi Euleri Opera Omnia (series 3). 12.
29. Brown, B.H. (1942). "The Euler-Diderot Anecdote". The American Mathematical Monthly. 49 (5): 302–303. {{cite journal}}: Unknown parameter |month= ignored (help)

Further reading

• Encyclopedia Britannica article
• Dunham, William (1999). Euler: The Master of Us All, Washington: Mathematical Association of America. ISBN 0-88385-328-0.
• Heimpell, Hermann, Theodor Heuss, Benno Reifenberg (editors). 1956. Die großen Deutschen, volume 2, Berlin: Ullstein Verlag.
• Krus, D.J. (2001) Is normal distribution due to Karl Gauss? Euler, his family of gamma functions, and place in history of statistics. Quality and Quantity: International Journal of Methodology, 35, 445-446.(Request reprint).
• O'Connor, John J.; Robertson, Edmund F., "Leonhard Euler", MacTutor History of Mathematics Archive, University of St Andrews
• Leonhard Euler at the Mathematics Genealogy Project
• Weisstein, Eric Wolfgang (ed.). "Euler, Leonhard (1707-1783)". ScienceWorld.
• Simmons, J. (1996). The giant book of scientists: The 100 greatest minds of all time, Sydney: The Book Company.
• Singh, Simon. (1997). Fermat's last theorem, Fourth Estate: New York, ISBN 1-85702-669-1
• Lexikon der Naturwissenschaftler, Spektrum Akademischer Verlag Heidelberg, 2000.
• Thiele, Rüdiger. (2005). The mathematics and science of Leonhard Euler, in Mathematics and the Historian's Craft: The Kenneth O. May Lectures, G. Van Brummelen and M. Kinyon (eds.), CMS Books in Mathematics, Springer Verlag. ISBN 0-387-25284-3.
• Wilson, Robert (2002): Euler (Gresham College lecture series)

External links

• Euler Archive
• A short biography of Euler

Template:Persondata

• 1707 births
• 1783 deaths
• 18th century mathematicians
• Blind people
• Calculating prodigies
• Calvinists
• Christians in science
• Christian mathematicians
• Dynamicists
• Number theorists
• Swiss mathematicians
• Swiss physicists
• People from Basel
• Music theorists
• Members of the Russian Academy of Sciences