Misplaced Pages

1/3–2/3 conjecture

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Unsolved problem on partial orders
A partial order formed by the series composition of one-element and three-element partial orders. Among its 27 linear extensions, the bottom left element occurs prior to the bottom right element in 9 out of 27. Partial orders with this structure are the only known extreme cases for the 1/3–2/3 conjecture.

In order theory, a branch of mathematics, the 1/3–2/3 conjecture states that, if one is comparison sorting a set of items then, no matter what comparisons may have already been performed, it is always possible to choose the next comparison in such a way that it will reduce the number of possible sorted orders by a factor of 2/3 or better. Equivalently, in every finite partially ordered set that is not totally ordered, there exists a pair of elements x and y with the property that at least 1/3 and at most 2/3 of the linear extensions of the partial order place x earlier than y.

Example

The partial order formed by three elements a, b, and c with a single comparability relationship, a ≤ b, has three linear extensions, a ≤ b ≤ c, a ≤ c ≤ b, and c ≤ a ≤ b. In all three of these extensions, a is earlier than b. However, a is earlier than c in only two of them, and later than c in the third. Therefore, the pair of a and c have the desired property, showing that this partial order obeys the 1/3–2/3 conjecture.

This example shows that the constants 1/3 and 2/3 in the conjecture are tight; if q is any fraction strictly between 1/3 and 2/3, then there would not exist a pair x, y in which x is earlier than y in a number of partial orderings that is between q and 1 − q times the total number of partial orderings.

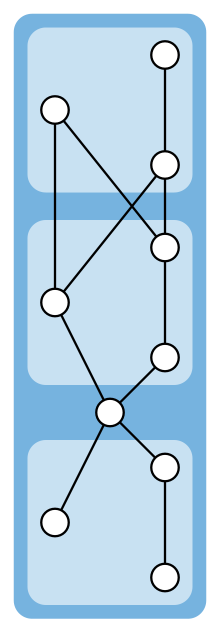
More generally, let P be any series composition of three-element partial orders and of one-element partial orders, such as the one in the figure. Then P forms an extreme case for the 1/3–2/3 conjecture in the sense that, for each pair x, y of elements, one of the two elements occurs earlier than the other in at most 1/3 of the linear extensions of P. Partial orders with this structure are necessarily series-parallel semiorders; they are the only known extreme cases for the conjecture and can be proven to be the only extreme cases with width two.

Definitions

A partially ordered set is a set X together with a binary relation ≤ that is reflexive, antisymmetric, and transitive. A total order is a partial order in which every pair of elements is comparable. A linear extension of a finite partial order is a sequential ordering of the elements of X, with the property that if x ≤ y in the partial order, then x must come before y in the linear extension. In other words, it is a total order compatible with the partial order. If a finite partially ordered set is totally ordered, then it has only one linear extension, but otherwise it will have more than one. The 1/3–2/3 conjecture states that one can choose two elements x and y such that, among this set of possible linear extensions, between 1/3 and 2/3 of them place x earlier than y, and symmetrically between 1/3 and 2/3 of them place y earlier than x.

There is an alternative and equivalent statement of the 1/3–2/3 conjecture in the language of probability theory. One may define a uniform probability distribution on the linear extensions in which each possible linear extension is equally likely to be chosen. The 1/3–2/3 conjecture states that, under this probability distribution, there exists a pair of elements x and y such that the probability that x is earlier than y in a random linear extension is between 1/3 and 2/3.

In 1984, Jeff Kahn and Michael Saks defined δ(P), for any partially ordered set P, to be the largest real number δ such that P has a pair x, y with x earlier than y in a number of linear extensions that is between δ and 1 − δ of the total number of linear extensions. In this notation, the 1/3–2/3 conjecture states that every finite partial order that is not total has δ(P) ≥ 1/3.

History

The 1/3–2/3 conjecture was formulated by Sergey Kislitsyn in 1968, and later made independently by Michael Fredman and by Nati Linial in 1984. It was listed as a featured unsolved problem at the founding of the journal Order, and remains unsolved; being called "one of the most intriguing problems in the combinatorial theory of posets."

A survey of the conjecture was produced in 1999.

Partial results

The 1/3–2/3 conjecture is known to be true for certain special classes of partial orders, including partial orders of width two, partial orders of height two, partial orders with at most 11 elements, partial orders in which each element is incomparable to at most six others, series-parallel partial orders, semiorders. and polytrees. In the limit as n goes to infinity, the proportion of n-element partial orders that obey the 1/3–2/3 conjecture approaches 100%.

In 1995, Graham Brightwell, Stefan Felsner, and William Trotter proved that, for any finite partial order P that is not total, δ(P) ≥ 1/2 − √5/10 ≈ 0.276. Their results improve previous weaker bounds of the same type. They use the probabilistic interpretation of δ(P) to extend its definition to certain infinite partial orders; in that context, they show that their bounds are optimal, in that there exist infinite partial orders with δ(P) = 1/2 − √5/10.

Applications

In 1984 Jeff Kahn and Saks proposed the following application for the problem: suppose one wishes to comparison sort a totally ordered set X, for which some partial order information is already known in the form of a partial order on X. In the worst case, each additional comparison between a pair x and y of elements may yield as little information as possible, by resolving the comparison in a way that leaves as many linear extensions as possible compatible with the comparison result. The 1/3–2/3 conjecture states that, at each step, one may choose a comparison to perform that reduces the remaining number of linear extensions by a factor of 2/3; therefore, if there are E linear extensions of the partial order given by the initial information, the sorting problem can be completed in at most log3/2E additional comparisons.

However, this analysis neglects the complexity of selecting the optimal pair x and y to compare. Additionally, it may be possible to sort a partial order using a number of comparisons that is better than this analysis would suggest, because it may not be possible for this worst-case behavior to occur at each step of a sorting algorithm. In this direction, it has been conjectured that logφE comparisons may suffice, where φ denotes the golden ratio.

A closely related class of comparison sorting problems was considered by Fredman in 1976, among them the problem of comparison sorting a set X when the sorted order of X is known to lie in some set S of permutations of X. Here S is not necessarily generated as the set of linear extensions of a partial order. Despite this added generality, Fredman showed that X can be sorted using log2|S| + O(|X|) comparisons, expressed in big O notation. This same bound applies as well to the case of partial orders and shows that log2E + O(n) comparisons suffice.

Generalizations and related results

In 1984, Kahn and Saks conjectured that, in the limit as w tends to infinity, the value of δ(P) for partially ordered sets of width w should tend to 1/2. In particular, they expect that only partially ordered sets of width two can achieve the worst case value δ(P) = 1/3, and in 1985 Martin Aigner stated this explicitly as a conjecture. The smallest known value of δ(P) for posets of width three is 14/39, and computer searches have shown that no smaller value is possible for width-3 posets with nine or fewer elements. Another related conjecture, again based on computer searches, states that there is a gap between 1/3 and the other possible values of δ(P): whenever a partial order does not have δ(P) exactly 1/3, it has δ(P) ≥ 0.348843.

Marcin Peczarski has formulated a "gold partition conjecture" stating that in each partial order that is not a total order one can find two consecutive comparisons such that, if ti denotes the number of linear extensions remaining after i of the comparisons have been made, then (in each of the four possible outcomes of the comparisons) t0 ≥ t1 + t2. If this conjecture is true, it would imply the 1/3–2/3 conjecture: the first of the two comparisons must be between a pair that splits the remaining comparisons by at worst a 1/3–2/3 ratio. The gold partition conjecture would also imply that a partial order with E linear extensions can be sorted in at most logφE comparisons; the name of the conjecture is derived from this connection with the golden ratio.

It is #P-complete, given a finite partial order P and a pair of elements x and y, to calculate the proportion of the linear extensions of P that place x earlier than y.

Notes

  1. Kahn & Saks (1984); Brightwell, Felsner & Trotter (1995).
  2. ^ Aigner (1985).
  3. ^ Brightwell, Felsner & Trotter (1995).
  4. ^ Kahn & Saks (1984)
  5. Kislitsyn (1968)
  6. However, despite the close connection of Fredman (1976) to the problem of sorting partially ordered data and hence to the 1/3–2/3 conjecture, it is not mentioned in that paper.
  7. Brightwell (1999)
  8. Linial (1984), Theorem 2; Sah (2021).
  9. ^ Trotter, Gehrlein & Fishburn (1992).
  10. ^ Peczarski (2006).
  11. ^ Peczarski (2008).
  12. Zaguia (2012).
  13. Brightwell (1989).
  14. Zaguia (2019).
  15. Brightwell, Felsner & Trotter (1995); Kahn & Saks (1984); Khachiyan (1989); Kahn & Linial (1991); Felsner & Trotter (1993).
  16. Fredman (1976)
  17. Kahn & Saks (1984).
  18. Saks (1985).
  19. Peczarski (2019).
  20. Brightwell & Winkler (1991).

References

Categories: