Misplaced Pages

Hamid Naderi Yeganeh
Naderi Yeganeh and a digital print of his artwork A Bird in Flight
Born	(1990-07-26) July 26, 1990 (age 34) Qom, Iran
Nationality	Iranian
Alma mater	Sharif University of Technology (M.Sc.) University of Qom (B.Sc.)
Known for	mathematical art
Awards	Gold medal of the 38th IMS competition Silver medals of the 38th IMS competition

Hamid Naderi Yeganeh (Persian: حمید نادری یگانه; born July 26, 1990, in Iran) is an Iranian mathematical artist and digital artist. He is known for using mathematical formulas to create drawings of real-life objects, intricate and symmetrical illustrations, animations, fractals and tessellations. Naderi Yeganeh uses mathematics as the main tool to create artworks. Therefore, his artworks can be totally described by mathematical concepts. Mathematical concepts he uses in his work include trigonometric functions, exponential function, Fibonacci sequence, sawtooth wave, etc.

His artwork 9,000 Ellipses was used as the background cover image of The American Mathematical Monthly – November 2017. His artwork Heart was used as the image for the February page of the 2016 Calendar of Mathematical Imagery published by the American Mathematical Society. His artwork Bird was used as the postcard image of the Art ∩ Math exhibit held at Center on Contemporary Art, Seattle in 2018. One of Naderi Yeganeh's artworks was used as the cover image for Newsletter of Iranian Mathematical Society, Autumn 2015. His works, including A Bird in Flight and Boat, have been used on several pages of the International Mathematical Knowledge Trust (IMKT)'s website. His art has also been featured in some school math textbooks including one that was published by Oxford University Press.

Education

Naderi Yeganeh received his bachelor's degree in mathematics from the University of Qom and a M.Sc. in pure mathematics from Sharif University of Technology. His MSc thesis was focused on numerical methods for approximation and visualization of invariant manifolds in dynamical systems. He won a gold medal at the 38th Iranian Mathematical Society’s nationwide mathematics competition held at Graduate University of Advanced Technology in May 2014 and a silver medal at the 39th IMS’s nationwide mathematics competition held at Yazd University in May 2015. A special report about University of Qom's achievements and statistics in the years between 2013 and 2020 issued by the university's budget management and published by the Iranian MSRT stated Naderi Yeganeh's winning a gold medal at the 38th IMS’s math competition as one of the five outstanding achievements of the university's students in the 2013-2020 period. According to one of the 38th IMS competition committee members, winning a gold medal by a student from University of Qom was a highlight of that competition.

Works

Drawings of real-life objects

Naderi Yeganeh has introduced two methods to draw real-life objects with mathematical formulas. By the first method, he creates tens of thousands of computer-generated mathematical figures to find a few interesting shapes accidentally. Then he changes the equations a little bit in order to increase the resemblance of the accidentally found shapes to real life objects. For example, by using this method, he found some shapes that resemble birds, fishes and sailing boats. In the second method, he draws a real life object with a step-by-step process. In each step, he tries to find out which mathematical formulas will produce the drawing. For example, by using this method, he drew birds in flight, butterflies, human faces and plants using trigonometric functions. Naderi Yeganeh says: "In order to create such shapes, it is very useful to know the properties of the trigonometric functions". In 2018, in an interview with the Sharif University of Technology Public Relations, Naderi Yeganeh said: I use mathematical concepts in a work of art in a way that it could be thoroughly explained in a paragraph. That makes the understanding of an artwork's scientific underpinning easier. More recently, he has introduced a method to describe an image pixel-by-pixel by using a network of mathematical functions.

A Bird in Flight

An instance of drawing real things by using Yeganeh's methods is A Bird in Flight, which is the name of a number of bird-like geometric shapes introduced by Naderi Yeganeh. Yeganeh created those drawings by using the two methods mentioned above. An example of A Bird in Flight that was created by his first method is made of 500 segments defined in a Cartesian plane where for each ${\displaystyle k=1,2,3,\ldots ,500}$ the endpoints of the ${\displaystyle k}$-th line segment are:

${\displaystyle \left({\frac {3}{2}}\sin ^{7}\left({\frac {2\pi k}{500}}+{\frac {\pi }{3}}\right),\,{\frac {1}{4}}\cos ^{2}\left({\frac {6\pi k}{500}}\right)\right)}$

and

${\displaystyle \left({\frac {1}{5}}\sin \left({\frac {6\pi k}{500}}+{\frac {\pi }{5}}\right),\,{\frac {-2}{3}}\sin ^{2}\left({\frac {2\pi k}{500}}-{\frac {\pi }{3}}\right)\right)}$.

The 500 line segments defined above together form a shape in the Cartesian plane that resembles a flying bird. Looking at the line segments on the wings of the bird causes an optical illusion and may trick the viewer into thinking that the line segments are curved lines. Therefore, the shape can also be considered as an optical artwork. Another version of A Bird in Flight that was designed by Naderi Yeganeh's second method is the union of all of the circles with center ${\displaystyle \left(A(k),B(k)\right)}$ and radius ${\displaystyle R(k)}$, where ${\displaystyle k=-10000,-9999,\ldots ,9999,10000}$, and

${\displaystyle A(k)={\frac {3k}{20000}}+\sin \left({\frac {\pi }{2}}\left({\frac {k}{10000}}\right)^{7}\right)\cos ^{6}\left({\frac {41\pi k}{10000}}\right)+{\frac {1}{4}}\cos ^{16}\left({\frac {41\pi k}{10000}}\right)\cos ^{12}\left({\frac {\pi k}{20000}}\right)\sin \left({\frac {6\pi k}{10000}}\right),}$

${\displaystyle {\begin{aligned}B(k)=&-\cos \left({\frac {\pi }{2}}\left({\frac {k}{10000}}\right)^{7}\right)\left(1+{\frac {3}{2}}\cos ^{6}\left({\frac {\pi k}{20000}}\right)\cos ^{6}\left({\frac {3\pi k}{20000}}\right)\right)\cos ^{6}\left({\frac {41\pi k}{10000}}\right)\\&+{\frac {1}{2}}\cos ^{10}\left({\frac {3\pi k}{100000}}\right)\cos ^{10}\left({\frac {9\pi k}{100000}}\right)\cos ^{10}\left({\frac {18\pi k}{100000}}\right),\\\end{aligned}}}$

${\displaystyle R(k)={\frac {1}{50}}+{\frac {1}{10}}\sin ^{2}\left({\frac {41\pi k}{10000}}\right)\sin ^{2}\left({\frac {9\pi k}{100000}}\right)+{\frac {1}{20}}\cos ^{2}\left({\frac {41\pi k}{10000}}\right)\cos ^{10}\left({\frac {\pi k}{20000}}\right).}$

The set of the 20,001 circles defined above form a subset of the Cartesian plane that resembles a flying bird. Although this version's equations are a lot more complicated than the version made of 500 segments, it has a far better resemblance to a real flying bird. It uses the periodic nature of trigonometric functions to form the feathers. Other works similar to this version of A Bird in Flight that was released by Naderi Yeganeh in 2016 are in the form of a flying parrot, magpie and stork.

Fractals and tessellations

Naderi Yeganeh has designed some fractals and tessellations inspired by the continents. For example, in 2015, he described the fractal Africa with an Africa-like octagon and its lateral inversion. And he has created tessellations with Northern America-like and South America-like polygons.

Fractal Africa

Fractal Africa is a fractal made of an infinite number of Africa-like octagons which was introduced by Naderi Yeganeh. The fractal's octagons are similar to each other and they have some resemblance to the map of Africa. The numbers of octagons of different sizes in the fractal is related to the Fibonacci sequence: 1, 2, 3, 5, 8, 13, 21, 34, .... The height of the biggest octagon of the fractal is φ times larger than the height of second octagon; where φ is the well-known golden ratio.

Exhibitions and conferences

• Art ∩ Math, Center on Contemporary Art (Seattle, WA), March 1 - April 14, 2018.
• The Intersection of Art + Math, Schack Art Center (Everett, WA), April 26 - June 2, 2018.
• LASER Talks in Tehran, Leonardo, the International Society for the Arts, Sciences and Technology (Tehran, Iran), August 10, 2018.

Reception

In 2015, CNN used the question "Is this the next da Vinci?" for the title of a video about Naderi Yeganeh's work and CNN Arabic used the title "Is this Iranian student da Vinci's successor?" for an article about him. In 2015, Asia Society Philippines stated in a post on Facebook that "Hamid Naderi Yeganeh reveals the beauty of Math through Art". In 2015, The National Museum of Mathematics stated in a post on Facebook that "Hamid Naderi Yeganeh takes graphing art to the next level!" In 2016, Institute for Mathematics and its Applications commented on the Naderi Yeganeh's blog post showing how to draw human faces with mathematical equations: "Another reason that math wins". In 2016, COSMOS raised this question in the introduction to its interview with Hamid Naderi Yeganeh: "Why couldn't high school mathematics be more like this?" in order to get its readers thinking about the potential of using Naderi Yeganeh's work in mathematics education. In 2016, Mathematics in Education and Industry stated in a tweet that: "Hamid Naderi Yeganeh is a mathematical artist who's created plant images by trigonometric functions." In 2016, Barbour Design Inc. stated on its own blog that "These often delicately intricate works are quite remarkable, and more astounding is that Yeganeh writes computer programs based on mathematical equations to produce them." In 2017, Mathematical Association of America commented about one of Naderi Yeganeh's animations in a tweet: "Watch the beauty of trigonometric functions come alive". In 2017, Fields Institute described Naderi Yeganeh's work as "beautiful math" in a tweet. In 2017, Berkeley Lab commented on one of Naderi Yeganeh's blog posts: "Create stunning symmetrical images armed with a few equations and a computer".

Views

Naderi Yeganeh believes that there are an infinite number of ways of using mathematical tools in art. In 2015, in an interview with CNN Style he said: "The power of mathematics is unlimited. There's an infinite number of great artworks that we can create". He says, "I don’t think computer-made art clashes with human creativity, but it can change the role of artists.” In 2016, He said in an interview with Dong-A Science: "For me, mathematics is the best tool to create works of art." Hamid Naderi Yeganeh believes that introducing mathematical objects that resemble real recognizable things may encourage young people to pursue mathematics. He believes mathematics is an international culture and mathematics can help to promote peace and love between nations. Naderi Yeganeh believes that Pi is an international number and it can be a symbol of peace between nations.

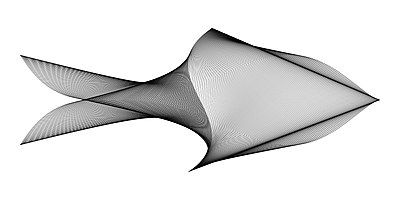
Gallery

Below are some examples of Yeganeh's mathematical figures:

References

1. "دانشگاه قم/مصاحبه با آقای..." (in Persian). University of Qom. Retrieved April 20, 2015.
2. ^ Zhao, Han (2018-05-07). "Can an algorithm be art?". Christian Science Monitor. ISSN 0882-7729. Archived from the original on 2018-05-08. Retrieved 2018-05-09.
3. Crum, Maddie (August 18, 2015). "These Delicate Drawings Are The Handiwork Of A Very Smart Computer". The Huffington Post. Archived from the original on August 21, 2015. Retrieved August 23, 2015.
4. ^ Smith, Belinda (February 29, 2016). "The art and beauty of mathematics". Cosmos. Archived from the original on May 14, 2016. Retrieved July 8, 2016.
5. "Inside Art" (PDF). STATure (STATistical Applications for Undergraduate Research Exploration). 1. McMaster University. April 2021. Archived (PDF) from the original on 2021-08-02. Retrieved 2021-08-14 – via MacSphere (McMaster University’s Institutional Repository).
6. MacDonald, Fiona (February 19, 2016). "7 times mathematics became art and blew our minds". Science Alert. Archived from the original on January 29, 2017. Retrieved January 23, 2017.
7. Grandi, C. (May 2020). "Using Art to Teach Mathematics". Mathematics in School. 49 (3). Mathematical Association: 2–7.
8. ^ Chung, Stephy (September 18, 2015). "Next da Vinci? Math genius using formulas to create fantastical works of art". CNN. Archived from the original on February 2, 2017. Retrieved January 23, 2017.
9. Haavisto, Aino (2022-08-04). "Ohjelmointi ja taide, osa 3: Taidetta laskukaavoilla" [Programming and art, part 3: Art with formulas]. Dimensiolehti (in Finnish). Matemaattisten Aineiden Opettajien Liitto MAOL ry. Retrieved 2022-08-07.
10. 林桂光 (24 October 2020). "編程的技術應用與學習表現" [Application of Programming Technology and Learning Performance]. MASTER-INSIGHT.COM (in Chinese). Archived from the original on 28 October 2020. Retrieved 27 October 2020.
11. "STEAM Series: Math and Art". West Windsor Arts Council. Archived from the original on 2019-07-29. Retrieved 2019-07-29.
12. Jalan, Atul (2019). Where Will Man Take Us?: The bold story of the man technology is creating. Penguin Random House India. ISBN 978-9-353-05505-9.
13. "Teaching Coding Languages in Noncoding Courses". New York University, Faculty of Arts & Science. September 6, 2019. Archived from the original on 19 October 2020. Retrieved 20 October 2020.
14. ^ Naderi Yeganeh, Hamid. "Importing Things From the Real World Into the Territory of Mathematics!". Huffington Post (blog). Archived from the original on 2015-12-18. Retrieved 2020-10-20.
15. ^ "Hamid Naderi Yeganeh: Fractal Africa". The De Morgan Forum – London Mathematical Society. September 21, 2016. Archived from the original on October 11, 2016. Retrieved October 10, 2016.
16. Tizón Escamilla, Nicolás. "Programación Didáctica de la materia Matemáticas Orientadas a las Enseñanzas Académicas correspondiente al Tercer Curso de Educación Secundaria Obligatoria" (PDF). University of Granada.
17. Naderi Yeganeh, Hamid (27 October 2015). "Using the Sawtooth Wave to Create Some Beautiful Images". HuffPost. Archived from the original on 24 October 2020. Retrieved 20 October 2020.
18. "About the Cover". The American Mathematical Monthly. 124 (9): 772. November 2017. doi:10.1080/00029890.2017.11919668. JSTOR 10.4169/amer.math.monthly.124.9.772. S2CID 218549565.
19. "AMM_Nov_2017.PNG" (PNG). Mathematical Association of America. Archived from the original on 1 November 2017. Retrieved 26 February 2020.
20. "Iranian Math Whiz Da Vinci Design on Cover of U.S. Mathematics Monthly". Kayhan. November 6, 2017. Archived from the original on January 26, 2018. Retrieved January 25, 2018.
21. Naderi Yeganeh, Hamid (November 10, 2016). "These Beautiful Images Are Created By Drawing Ellipses". Huffington Post (blog). Archived from the original on December 11, 2015. Retrieved December 1, 2017.
22. "2016 Calendar of Mathematical Imagery". American Mathematical Society. Archived from the original on December 23, 2016.
23. "چاپ تصویر ابداعی دانشجوی نابغه ایرانی در تقویم 2016 انجمن ریاضی آمریکا" [Publication of an Innovative Image of an Iranian Genius Student in the American Mathematical Society's 2016 Calendar] (in Persian). Islamic Azad University, Central Tehran Branch. January 2, 2016. Archived from the original on 25 February 2020. Retrieved 26 February 2020.
24. "February 2018". Surface Design Association–Washington. 22 February 2018. Archived from the original on 25 February 2020. Retrieved 25 February 2020.
25. @CoCASeattle (February 21, 2018). "CoCA's next show Art n Math explores the bold new realms in math and art. Opening reception on Thurs, March 1, 6pm – 9pm" (Tweet). Archived from the original on March 10, 2020 – via Twitter.
26. @uwnews (March 14, 2018). "In celebration of #PiDay, @UW alums — and former #math instructors — Katherine Cook and Dan Finkel (@MathforLove) will present "The Beauty of Math" tonight at @CoCASeattle" (Tweet). Archived from the original on March 10, 2020 – via Twitter.
27. ^ "خلق آثار هنری به وسیله ی فرمول های ریاضی" [Creating Works of Art with Mathematical Formulas] (PDF). Newsletter of Iranian Mathematical Society (in Persian). Vol. 36, no. 3. Autumn 2015. Archived (PDF) from the original on June 28, 2017. Retrieved February 23, 2020.
28. "Mathematics Portal - IMKT". International Mathematical Knowledge Trust. Archived from the original on 24 February 2020. Retrieved 24 February 2020.
29. "About IMKT". International Mathematical Knowledge Trust. Archived from the original on 24 February 2020. Retrieved 24 February 2020.
30. "Portal {OLD}". International Mathematical Knowledge Trust. Retrieved 24 February 2020.
31. "Department News, January 2024, Part 2". University College London Department of Mathematics. 2024-01-25. Retrieved 2024-07-18.
32. "Oxford University Press adorns book with Iranian mathematical artist's illustration". Center of International Science and Technology Cooperations. January 18, 2024.
33. ^ "آمیزه ریاضی و هنر" [Combination of Mathematics and Art] (PDF). Sharif Daily (in Persian). 737. Sharif University of Technology: 2. November 7, 2017. Archived (PDF) from the original on 18 August 2020. Retrieved 18 August 2020.
34. "Hamid Naderi Yeganeh". about.me. Archived from the original on May 26, 2018. Retrieved December 23, 2019.
35. "وقتی علم و هنر با هم آمیخته میشوند - مصاحبه ای با حمید نادری یگانه" [Interview with Hamid Naderi Yeganeh: When Art and Science Blend Together] (PDF). گاهنامه کانون هنرهای تجسمی دانشگاه صنعتی شریف [Periodical of Sharif Visual Arts Center] (in Persian). Sharif University of Technology Visual Arts Center. Archived (PDF) from the original on 2019-03-09. Retrieved 2019-12-30.
36. "Numerical Methods for Approximation and Visualization of Invariant Manifolds in Dynamical Systems, Author: Naderi Yeganeh, Hamid, Publisher: Sharif University of Technology, 2019". Sharif Digital Repository. Sharif University of Technology. Archived from the original on 19 Aug 2021.
37. "ESMA Newsletter February 2015" (PDF). ESMA European Society for Mathematics and the Arts. February 2015. Archived (PDF) from the original on April 2, 2015. Retrieved March 19, 2015.
38. "Math Art: Hamid Naderi Yeganeh". Washington University in St. Louis. February 2015. Archived from the original on February 20, 2015. Retrieved March 19, 2015.
39. "سی و هشتمین مسابقه ریاضی دانشجویی کشور، دانشگاه تحصيلات تكميلي صنعتي و فناوري پيشرفته ماهان، 23-26 اردیبهشت 1393، نتایج انفرادی" [The Country's 38th Students Mathematics Competition, Graduate University of Advanced Technology, 23-26 Ordibehesht 1393, Individual Results] (PDF) (in Persian). Iranian Mathematical Society. May 2014. Archived (PDF) from the original on March 4, 2016. Retrieved February 23, 2020.
40. "سی ونهمین مسابقه ریاضی دانشجویی کشور، دانشگاه یزد، 22-25 اردیبهشت 1394، نتایج انفرادی" [The Country's 39th Students Mathematics Competition, Yazd University, 22-25 Ordibehesht 1394, Individual Results] (PDF) (in Persian). Iranian Mathematical Society. May 2015. Archived (PDF) from the original on May 17, 2015. Retrieved May 18, 2015.
41. "دانشگاه قم از نگاه آمار دوره گزارش از 1392 تا 1399" [University of Qom in terms of statistics (reporting period from 2013 to 2020)] (PDF). Iranian Ministry of Science, Research and Technology (in Persian). 2021. p. 26. Archived (PDF) from the original on August 19, 2021.
42. Ahmadi, Bijan (Spring 2014). "چند نکته در مورد مسابقه امسال" [A Few Points About the Competition] (PDF). Newsletter of Iranian Mathematical Society (in Persian). 141. Iranian Mathematical Society: 32. Archived (PDF) from the original on 19 August 2021. Retrieved 19 August 2021.
43. Young, Lauren (January 19, 2016). "Math Is Beautiful". Science Friday. Archived from the original on January 29, 2017. Retrieved January 23, 2017.
44. La-Gaffe, Gaston (2021-12-13). "Top 5 Expressions of Mathematics in Art". FAD Magazine. Archived from the original on April 21, 2022. Retrieved 2022-04-21.
45. Fratini, Stephen (2021). "5.9.6 Hamid Naderi Yeganeh". Math in Art, and Art in Math. Independently published. ISBN 979-8-7308-3170-4.
46. ^ Bellos, Alex (February 24, 2015). "Catch of the day: mathematician nets weird, complex fish". The Guardian. Archived from the original on November 30, 2016.
47. Cavanagh, Peter (March 5, 2021). Avian Arithmetic: The mathematics of bird flight (Speech). National Museum of Mathematics' Events. MoMath Online, NY, United States. Archived from the original on 5 April 2021. Retrieved 5 April 2021.
48. Mellow, Glendon (August 6, 2015). "Mathematically Precise Crosshatching". Scientific American (blog). Archived from the original on September 25, 2015. Retrieved August 11, 2015.
49. "This is not a bird (or a moustache)". Plus Magazine. January 8, 2015. Archived from the original on April 23, 2015. Retrieved April 22, 2015.
50. ^ Naderi Yeganeh, Hamid (January 9, 2017). "How to Draw with Math". Scientific American (blog). Archived from the original on February 2, 2017. Retrieved January 23, 2017.
51. ^ Naderi Yeganeh, Hamid (January 12, 2016). "Drawing Birds in Flight With Mathematics". Huffington Post (blog). Archived from the original on February 2, 2017. Retrieved January 23, 2017.
52. ^ "Mathematical Concepts Illustrated by Hamid Naderi Yeganeh". American Mathematical Society. Archived from the original on July 29, 2019. Retrieved July 29, 2019.
53. Naderi Yeganeh, Hamid (March 8, 2016). "Drawing Human Faces With Mathematics". Huffington Post (blog). Archived from the original on February 2, 2017. Retrieved January 23, 2017.
54. Antonick, Gary (June 6, 2016). "The Candy Store". The New York Times. Archived from the original on 27 February 2020. Retrieved 27 February 2020.
55. ^ "Von Formeln und Vögeln". Spektrum der Wissenschaft (in German). 05/2021: 47. February 4, 2021. ISSN 0170-2971. Archived from the original on 7 February 2021. Retrieved 7 February 2021.
56. Baugher, Janée J. (2020). The Ekphrastic Writer: Creating Art-Influenced Poetry, Fiction and Nonfiction. McFarland and Company, Inc., Publishers. p. 56. ISBN 9781476639611. Archived from the original on 2020-09-27. Retrieved 2020-08-05.
57. "انتشار اثر دانشجوی صنعتی شریف در ماهنامه ریاضی". Telegram (in Persian). Sharif University of Technology Public Relations. Archived from the original on 25 December 2020. Retrieved 25 December 2020.
58. Naderi Yeganeh, Hamid (2025-01-02). "Pictures from Networks of Mathematical Functions". Math Horizons. 32 (1): 22–23. doi:10.1080/10724117.2024.2368373. ISSN 1072-4117.
59. Mellow, Glendon (August 6, 2015). "Mathematically Precise Crosshatching". Scientific American (blog). Archived from the original on September 25, 2015. Retrieved August 11, 2015.
60. "เมื่อคณิตศาสตร์ถูกสร้างเป็นภาพศิลปะ" [When Mathematics is Made into Art]. Faculty of Fine and Applied Arts (in Thai). Chulalongkorn University. Archived from the original on 2021-08-19. Retrieved 2021-10-03.
61. Gutiérrez Gómez, Margarita (2023). Artemáticas (in Spanish). Spain: Letrame Grupo Editorial. p. 135. ISBN 978-84-1144-491-0.
62. Antonick, Gary (April 13, 2015). "The Tax Collector". The New York Times (blog). Archived from the original on April 20, 2015. Retrieved April 20, 2015.
63. "Continents, Math Explorers' Club, and "I use math for…"". mathmunch.org. April 2015. Archived from the original on April 16, 2015. Retrieved April 20, 2015.
64. "با دنیای آدم های نابغه آشنا شویم، داوینچی ایرانی با فرمول ریاضی تابلو می کشد" [Learn about the world of geniuses, The Iranian da Vinci Draws Paintings by Mathematical Formulas] (PDF). اصفهان زیبا [The Beautiful Isfahan] (in Persian). Isfahan. October 20, 2015. Archived (PDF) from the original on February 23, 2020. Retrieved February 23, 2020.
65. ^ McDonald, Glenn (April 14, 2016). "Math Artist Finds the Beauty in Equations: Photos". Seeker. Archived from the original on 23 February 2020. Retrieved 23 February 2020.
66. Ouellette, Jennifer (February 28, 2015). "Physics Week in Review: February 28, 2015". Scientific American. Archived from the original on August 15, 2020. Retrieved 3 January 2021.
67. Paul, James (2024-04-12). "Mathematician Draws Sea Waves With Equations; Amused Internet Has Plenty Of Questions". Mashable India. Archived from the original on 2024-04-12. Retrieved 2024-04-12.
68. C.I.P. Citizens In Power (January 2020). "TOOL 7: A SYNCHRONOUS EXHIBITION OF ARTMATH MASTERPIECES" (PDF). The Art Of Maths. p. 9. Archived (PDF) from the original on 2 January 2021. Retrieved 21 March 2021.
69. Antonick, Gary (10 August 2015). "John Conway's Wizard Puzzle". The New York Times. Archived from the original on 12 November 2020. Retrieved 3 January 2021.
70. "Art ∩ Math". CoCA Seattle. Archived from the original on 2018-06-23. Retrieved 2018-06-04.
71. "The Intersection of Art + Math | Exhibit | Schack Art Center". www.schack.org. Archived from the original on 2018-06-02. Retrieved 2018-06-04.
72. "LASER Talks in Tehran". Leonardo/ISAST. Archived from the original on 2018-08-14. Retrieved 2018-08-13.
73. "Math genius and artist: Is this the next da Vinci?". CNN. September 17, 2015. Archived from the original on 2 March 2020. Retrieved 2 March 2020.
74. "AMS: Math Digest - September 2015: On Hamid Naderi Yeganeh's mathematical art". American Mathematical Society. Archived from the original on 2 March 2020. Retrieved 2 March 2020.
75. "هل هذا الطالب الإيراني هو خليفة ليوناردو دافنشي؟" [Is this Iranian student da Vinci's successor?]. CNN Arabic (in Arabic). 2015-09-21. Archived from the original on 2021-05-13. Retrieved 2021-10-17.
76. "Iranian student Hamid Naderi Yeganeh reveals the beauty of Math through Art". Facebook. Asia Society Philippines. September 25, 2015. Archived from the original on 2 March 2020. Retrieved 2 March 2020.
77. "수학적 아름다움, 프랙털 아트의 세계" [Mathematical beauty, the world of fractal art]. Sciencetimes (in Korean). 8 December 2020. Archived from the original on 8 December 2020. Retrieved 8 December 2020.
78. "Hamid Naderi Yeganeh takes graphing art to the next level! ..." Facebook. National Museum of Mathematics. September 26, 2015. Archived from the original on 2 March 2020. Retrieved 2 March 2020.
79. @ima_umn (March 9, 2016). "Another reason that #math wins - Drawing Human Faces With Mathematics..." (Tweet). Archived from the original on March 10, 2020 – via Twitter.
80. "Resources". Inspiring Mathematics and Science in Teacher Education. 7 July 2016. Archived from the original on 12 March 2020. Retrieved 12 March 2020.
81. @MEIMaths (January 26, 2016). "Hamid Naderi Yeganeh is a mathematical artist who's created plant images by trigonometric functions. See more of..." (Tweet). Archived from the original on March 10, 2020 – via Twitter.
82. "The Beauty of Math". Barbour Design Inc. April 5, 2016. Archived from the original on 2 March 2020. Retrieved 2 March 2020.
83. @maanow (May 26, 2017). "Watch the beauty of trigonometric functions come alive" (Tweet) – via Twitter.
84. @FieldsInstitute (October 26, 2017). "Beautiful math..." (Tweet) – via Twitter.
85. @BerkeleyLab (March 21, 2017). "Create stunning symmetrical images armed with a few equations & a computer ..." (Tweet) – via Twitter.
86. Cook, Katherine; Finkel, Dan (2018-03-13). Art N Math. Center on Contemporary Art. ISBN 9780999081921.
87. "The Power of Mathematics is Unlimited!". Mathnasium. September 26, 2015. Archived from the original on 20 March 2020. Retrieved 20 March 2020.
88. 조혜인 (July 2016). "그래프의 화려한 변신". 수학동아 (Dong-A Mathematics) (in Korean). 082. The Dong-a Ilbo: 62–65. ISSN 2092-6693. Archived from the original on 16 March 2020. Retrieved 16 March 2020.
89. Knowles, Elizabeth (February 3, 2016). "When Math Transforms into Art". The Science Explorer. LabX Media Group. Archived from the original on 29 October 2019. Retrieved 12 March 2020.
90. Pedersen, Alex (18 May 2016). "CREATORS – HAMID NADERI YEGANEH". Art the Science. Archived from the original on 25 February 2020. Retrieved 25 February 2020.

External links

• Mathematical Concepts Illustrated by Hamid Naderi Yeganeh at American Mathematical Society
• Hamid Naderi Yeganeh's blog posts in The Huffington Post
• http://alum.sharif.edu/~naderiyeganeh

v t e Mathematics in Iran
Mathematicians	Before 20th Century Abu al-Wafa' Buzjani Jamshid al-Kashi (al-Kashi's theorem) Omar Khayyam (Khayyam-Pascal's triangle, Khayyam-Saccheri quadrilateral, Khayyam's Solution of Cubic Equations) Al-Mahani Muhammad Baqir Yazdi Nizam al-Din al-Nisapuri Al-Nayrizi Kushyar Gilani Ayn al-Quzat Hamadani Al-Isfahani Al-Isfizari Al-Khwarizmi (Al-jabr) Najm al-Din al-Qazwini al-Katibi Nasir al-Din al-Tusi Al-Biruni Modern Maryam Mirzakhani Caucher Birkar Sara Zahedi Farideh Firoozbakht (Firoozbakht's conjecture) S. L. Hakimi (Havel–Hakimi algorithm) Siamak Yassemi Freydoon Shahidi (Langlands–Shahidi method) Hamid Naderi Yeganeh Esmail Babolian Ramin Takloo-Bighash Lotfi A. Zadeh (Fuzzy mathematics, Fuzzy set, Fuzzy logic) Ebadollah S. Mahmoodian Reza Sarhangi (The Bridges Organization) Siavash Shahshahani Gholamhossein Mosaheb Amin Shokrollahi Reza Sadeghi Mohammad Mehdi Zahedi Mohsen Hashtroodi Hossein Zakeri Amir Ali Ahmadi
Prize Recipients	Fields Medal Maryam Mirzakhani (2014) Caucher Birkar (2018) EMS Prize Sara Zahedi (2016) Satter Prize Maryam Mirzakhani (2013)
Organizations	Iranian Mathematical Society
Institutions	Institute for Research in Fundamental Sciences

v t e Mathematics and art
Concepts	Algorithm Catenary Fractal Golden ratio Hyperboloid structure Minimal surface Paraboloid Perspective Camera lucida Camera obscura Plastic ratio Projective geometry Proportion Architecture Human Symmetry Tessellation Wallpaper group
Forms	Algorithmic art Anamorphic art Architecture Geodesic dome Pyramid Vastu shastra Computer art Fiber arts 4D art Fractal art Islamic geometric patterns Girih Jali Muqarnas Zellij Knotting Celtic knot Croatian interlace Interlace Music Origami Mathematics Sculpture String art String figure Tiling
Artworks	List of works designed with the golden ratio Continuum Mathemalchemy Mathematica: A World of Numbers... and Beyond Octacube Pi Pi in the Sky
Buildings	Cathedral of Saint Mary of the Assumption Hagia Sophia Kresge Auditorium Pantheon Parthenon Pyramid of Khufu Sagrada Família Sydney Opera House Taj Mahal
Artists	Renaissance Paolo Uccello Piero della Francesca Leonardo da Vinci Vitruvian Man Albrecht Dürer Parmigianino Self-portrait in a Convex Mirror 19th–20th Century William Blake The Ancient of Days Newton Jean Metzinger Danseuse au café L'Oiseau bleu Giorgio de Chirico Man Ray M. C. Escher Circle Limit III Print Gallery Relativity Reptiles Waterfall René Magritte La condition humaine Salvador Dalí Crucifixion The Swallow's Tail Crockett Johnson Contemporary Max Bill Martin and Erik Demaine Scott Draves Jan Dibbets John Ernest Helaman Ferguson Peter Forakis Susan Goldstine Bathsheba Grossman George W. Hart Desmond Paul Henry Anthony Hill Charles Jencks Garden of Cosmic Speculation Andy Lomas Robert Longhurst Jeanette McLeod Hamid Naderi Yeganeh István Orosz Hinke Osinga Antoine Pevsner Tony Robbin Alba Rojo Cama Reza Sarhangi Oliver Sin Hiroshi Sugimoto Daina Taimiņa Roman Verostko Margaret Wertheim
Theorists	Ancient Polykleitos Canon Vitruvius De architectura Renaissance Filippo Brunelleschi Leon Battista Alberti De pictura De re aedificatoria Piero della Francesca De prospectiva pingendi Luca Pacioli De divina proportione Leonardo da Vinci A Treatise on Painting Albrecht Dürer Vier Bücher von Menschlicher Proportion Sebastiano Serlio Regole generali d'architettura Andrea Palladio I quattro libri dell'architettura Romantic Samuel Colman Nature's Harmonic Unity Frederik Macody Lund Ad Quadratum Jay Hambidge The Greek Vase Modern Owen Jones The Grammar of Ornament Ernest Hanbury Hankin The Drawing of Geometric Patterns in Saracenic Art G. H. Hardy A Mathematician's Apology George David Birkhoff Aesthetic Measure Douglas Hofstadter Gödel, Escher, Bach Nikos Salingaros The 'Life' of a Carpet
Publications	Journal of Mathematics and the Arts Lumen Naturae Making Mathematics with Needlework Rhythm of Structure Viewpoints: Mathematical Perspective and Fractal Geometry in Art
Organizations	Ars Mathematica The Bridges Organization European Society for Mathematics and the Arts Goudreau Museum of Mathematics in Art and Science Institute For Figuring Mathemalchemy National Museum of Mathematics
Related	Droste effect Mathematical beauty Patterns in nature Sacred geometry
Category

• Mathematics
• Biography
• Arts

• Mathematical artists
• Digital artists
• Living people
• Iranian designers
• Fractal artists
• Iranian contemporary artists
• 1990 births
• Sharif University of Technology alumni
• Iranian Mathematics Competition Medalists
• 21st-century Iranian mathematicians
• 21st-century male artists
• People from Qom
• HuffPost bloggers