This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Acoustic tweezers (also known as acoustical tweezers) are a set of tools that use sound waves to manipulate the position and movement of very small objects. Strictly speaking, only a single-beam based configuration can be called acoustical tweezers. However, the broad concept of acoustical tweezers involves two configurations of beams: single beam and standing waves. The technology works by controlling the position of acoustic pressure nodes that draw objects to specific locations of a standing acoustic field. The target object must be considerably smaller than the wavelength of sound used, and the technology is typically used to manipulate microscopic particles.
Acoustic waves have been proven safe for biological objects, making them ideal for biomedical applications. Recently, applications for acoustic tweezers have been found in manipulating sub-millimetre objects, such as flow cytometry, cell separation, cell trapping, single-cell manipulation, and nanomaterial manipulation. The use of one-dimensional standing waves to manipulate small particles was first reported in the 1982 research article "Ultrasonic Inspection of Fiber Suspensions".
Method

In a standing acoustic field, objects experience an acoustic-radiation force that moves them to specific regions of the field. Depending on an object's properties, such as density and compressibility, it can be induced to move to either acoustic pressure nodes (minimum pressure regions) or pressure antinodes (maximum pressure regions). As a result, by controlling the position of these nodes, the precise movement of objects using sound waves is feasible. Acoustic tweezers do not require expensive equipment or complex experimental setups.
Fundamental theory
Particles in an acoustic field can be moved by forces originating from the interaction among the acoustic waves, fluid, and particles. These forces (including acoustic radiation force, secondary field force between particles, and Stokes drag force) create the phenomena of acoustophoresis, which is the foundation of the acoustic tweezers technology.
Acoustic radiation force
Main article: Acoustic radiation forceWhen a particle is suspended in the field of a sound wave, an acoustic radiation force that has risen from the scattering of the acoustic waves is exerted on the particle. This was first modeled and analyzed for incompressible particles in an ideal fluid by Louis King in 1934. Yosioka and Kawasima calculated the acoustic radiation force on compressible particles in a plane wave field in 1955. Gorkov summarized the previous work and proposed equations to determine the average force acting on a particle in an arbitrary acoustical field when its size is much smaller than the wavelength of the sound. Recently, Bruus revisited the problem and gave detailed derivation for the acoustic radiation force.

As shown in Figure 1, the acoustic radiation force on a small particle results from a non-uniform flux of momentum in the near-field region around the particle, , which is caused by the incoming acoustic waves and the scattering on the surface of the particle when acoustic waves propagate through it. For a compressible spherical particle with a diameter much smaller than the wavelength of acoustic waves in an ideal fluid, the acoustic radiation force can be calculated by , where is a given quantity, also called acoustic potential energy. The acoustic potential energy is expressed as:
where
- is the particle volume,
- is the acoustic pressure,
- is the velocity of acoustic particles,
- is the fluid mass density,
- is the speed of sound of the fluid,
- is the time-average term,
The coefficients and can be calculated by and
where
- is the mass density of the particle,
- is the speed of sound of the particle.
Acoustic radiation force in standing waves
The standing waves can form a stable acoustic potential energy field, so they are able to create stable acoustic radiation force distribution, which is desirable for many acoustic tweezers applications. For one-dimension planar standing waves, the acoustic fields are given by:
,
,
,
where
- is the displacement of acoustic particle,
- is the acoustic pressure amplitude,
- is the angular velocity,
- is the wave number.
With these fields, the time-average terms can be obtained. These are:
,
,
Thus, the acoustic potential energy is:
,
Then, the acoustic radiation force is found by differentiation:
,
, ,
where
- is the acoustic energy density, and
- is acoustophoretic contrast factor.
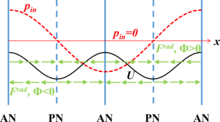
The term shows that the radiation force period is one-half of the pressure period. Also, the contrast factor can be positive or negative depending on the properties of particles and fluid. For positive value of , the radiation force points from the pressure antinodes to the pressure nodes, as shown in Figure 2, and the particles will be pushed to the pressure nodes.
Secondary acoustic forces
When multiple particles in a suspension are exposed to a standing wave field, they will not only experience acoustic radiation force, but also secondary acoustic forces caused by waves scattered by other particles. The inter-particle forces are sometimes called Bjerknes forces. A simplified equation for the inter-particle forces of identical particles is:
where
- is the radius of the particle,
- is the distance between the particles,
- is the angle between the central line of the particles and the direction of propagation of the incident acoustic wave.
The sign of the force represents its direction: a negative sign for an attractive force, and a positive sign for a repulsive force. The left side of the equation depends on the acoustic particle velocity amplitude and the right side depends on the acoustic pressure amplitude . The velocity-dependent term is repulsive when particles are aligned with wave propagation (Θ=0°), and negative when perpendicular to wave propagation (Θ=90°). The pressure-dependent term is unaffected by the particle orientation and is always attractive. In the case of a positive contrast factor, the velocity-dependent term diminishes as particles are driven to the velocity node (pressure antinode), as in the case of air bubbles and lipid vesicles. In a similar way, the pressure-dependent term diminishes as particles are driven towards the pressure node (velocity antinode), as are most solid particles in aqueous solutions.
In addition to the scattering-related secondary acoustic forces, the flow field resulting from the interactions of the various acoustic streaming fields, generated by the acoustic boundary layer of each particle (sometimes called microstreaming), can induce additional viscous shear forces on each of the particles' surfaces, which then results in an additional contribution to the secondary acoustic forces in its fully viscous formulations. The viscous effects on the secondary acoustic force can become significant when compared to the perfect fluid formulation exemplified above, and even dominant in certain limit cases, yielding both quantitatively and qualitatively different results than what is predicted by inviscid theory. The relevance of the viscous contributions varies greatly depending on the specific case being investigated, and thus important care needs to be taken in selecting an appropriate secondary acoustic force model for the given scenario.
The influence of the secondary forces is usually very weak, and only has an effect when the distance between particles is very small. It becomes important in aggregation and sedimentation applications, where particles are initially gathered in nodes by the acoustic radiation force. As inter-particle distances become smaller, the secondary forces assist in further aggregation until the clusters become heavy enough for sedimentation to begin.
Acoustic streaming
Main article: Acoustic streamingAcoustic streaming is a steady flow generated by the nonlinear component of the oscillations in an acoustic field. Depending on the mechanisms, the acoustic streaming can be categorized into two general types, Eckart streaming and Rayleigh streaming. Eckart streaming is driven by a time-average momentum flux created when high-amplitude acoustic waves propagate and attenuate in a fluid. Rayleigh streaming, also called "boundary driven streaming", is forced by Reynolds stresses in the viscous boundary layer. Both of the driven mechanisms come from a time-average nonlinear effect.
A perturbation approach is used to analyze the phenomenon of nonlinear acoustic streaming. The governing equations for this problem are mass conservation and Navier-Stokes equations:
,
where
- is the density of fluid,
- is the velocity of fluid particle,
- is the pressure,
- is the dynamic viscosity of fluid,
- is the viscosity ratio.
The perturbation series can be written as , , , which are diminishing series with the higher-order terms much smaller than the lower-order ones.
The liquid is quiescent and homogeneous at its zero-order state. Substituting the perturbation series into the mass conservation and Navier-Stokes equation and using the relation of , the first-order equations can be obtained by collecting terms in first-order,
,
.
Similarly, the second-order equations can be found as well,
,
.
For the first-order equations, taking the time derivation of the Navier-Stokes equation and inserting the mass conservation, a combined equation can be found:
.
This is an acoustic wave equation with viscous attenuation. Physically, and can be interpreted as the acoustic pressure and the velocity of the acoustic particle.
The second-order equations can be considered as governing equations used to describe the motion of fluid with mass source and force source . Generally, the acoustic streaming is a steady mean flow, where the response time scale is much smaller than the one of the acoustic vibration. The time-average term is normally used to present the acoustic streaming. By using , the time-average second-order equations can be obtained:
,
.
It is important to note that the time-averaging of pure first-order terms lead to their cancellation, since they are by definition harmonic. This means that they are pure sine waves, and thus have a mean of 0, which leads to the cancellation of any term that contains them. Second-order terms are, however, not harmonic, and do not get cancelled out by time-averaging. This is most important for understanding acoustic streaming: first-order terms, related to simple oscillatory motion, have much larger magnitudes than second-order terms, and thus are dominant in the oscillation time-scale. Those first-order terms, however, being pure sines, in a quasi-steady state, repeat after each oscillation cycle, yielding no net fluid flow. Second-order terms, instead, are not harmonic, and thus can have a cumulative effect which, despite being smaller, can add up over many oscillation cycles, leading to the development of the net steady-state flow we identify as acoustic streaming.
In determining the acoustic streaming, the second-order equations are thus most important. Since Navier-Stokes equations can only be analytically solved for simple cases, numerical methods are typically used, with the finite element method (FEM) the most common technique. It can be employed to simulate the acoustic streaming phenomena. Figure 3 is one example of acoustic streaming around a solid circular pillar, which is calculated by FEM.
As mentioned, acoustic streaming is driven by mass and force sources originating from the acoustic attenuation. However, these are not the only driven forces for acoustic streaming. The boundary vibration may also contribute, especially to "boundary driven streaming". For these cases, the boundary condition should also be processed by the perturbation approach and be imposed on the two order equations accordingly.
Particle motion
The motion of a suspended particle whose gravity is balanced by the buoyancy force in an acoustic field is determined by two forces: the acoustic radiation force and Stokes drag force. By applying Newton's law, the motion can be described as:
,
.
where
- is the fluid velocity,
- is the velocity of particle.
For applications in a static flow, the fluid velocity comes from the acoustic streaming. The magnitude of acoustic streaming depends on the power and frequency of the input and the properties of the fluid media. For typical acoustic-based microdevices, the operating frequency may be from the kHz to the MHz range. The vibration amplitude is in a range of 0.1 nm to 1 μm. Assuming the fluid used is water, the estimated magnitude of acoustic streaming is in the range of 1 μm/s to 1 mm/s. Thus, the acoustic streaming should be smaller than the main flow for most continuous flow applications. The drag force is mainly induced by the main flow in those applications.
Applications
This section has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Cell separation
Cells with different densities and compression strengths can theoretically be separated with acoustic force. It has been suggested that acoustic tweezers could be used to separate lipid particles from red blood cells. This is a problem during cardiac surgery supported by a heart-lung machine, for which current technologies are insufficient. According to the proposal, acoustic force applied to blood plasma passing through a channel will cause red blood cells to gather in the pressure node in the center and the lipid particles to gather in antinodes at the sides (see Figure 4). At the end of the channel, the separated cells and particles exit through separate outlets.
The acoustic method might also be used to separate particles of different sizes. According to the equation of primary acoustic radiation force, larger particles experience larger forces than smaller particles. Shi et al. reported using interdigital transducers (IDTs) to generate a standing surface acoustic wave (SSAW) field with pressure nodes in the middle of a microfluidic channel, separating microparticles with different diameters. When introducing a mixture of particles with different sizes from the edge of the channel, larger particles will migrate toward the middle more quickly and be collected at the center outlet. Smaller particles will not be able to migrate to the center outlet before they are collected from the side outlets. This experimental setup has also been used to separate blood components, bacteria, and hydrogel particles.
3D cell focusing
Fluorescence-activated cell sorters (FACS) can sort cells by focusing a fluid stream containing the cells, detecting fluorescence from individual cells, and separating the cells of interest from other cells. They have high throughput but are expensive to purchase and maintain, and are bulky with a complex configuration. They also affect cell physiology with high shear pressure, impact forces and electromagnetic forces, which may result in cellular and genetic damage. Acoustic forces are not dangerous to cells, and there has been progress integrating acoustic tweezers with optical/electrical modules for simultaneous cell analysis and sorting, in a smaller and less-expensive machine.
Acoustic tweezers have been developed to achieve 3D focusing of cells/particles in microfluidics. A pair of interdigital transducers (IDTs) are deposited on a piezoelectric substrate, and a microfluidic channel is bonded with the substrate and positioned between the two IDTs. Microparticle solutions are infused into the microfluidic channel by a pressure-driven flow. Once an RF signal is applied to both IDTs, two series of surface acoustic waves (SAW) propagate in opposite directions toward the particle suspension solution inside the microchannel. The constructive interference of the two SAWs results in the formation of a SSAW. Leakage waves in the longitudinal mode are generated inside the channel, causing pressure fluctuations that act laterally on the particles. As a result, the suspended particles inside the channel will be forced toward either the pressure nodes or antinodes, depending on the density and compressibility of the particles and the medium. When the channel width covers only one pressure node (or antinode), the particles will be focused in that node.
In addition to focusing in a horizontal direction, cells/particles can also be focused in the vertical direction. After SSAW is on, the randomly distributed particles are focused into a single file stream (Fig. 10c) in the vertical direction. By integrating a standing surface acoustic wave (SSAW)-based microdevice capable of 3D particle/cell focusing with laser-induced fluorescence (LIF) detection system, acoustic tweezers are developed into a microflow cytometer for high-throughput single cell analysis.
The tunability offered by chirped interdigital transducers renders it capable of precisely sorting cells into a number (e.g., five) of outlet channels in a single step. This is a major advantage over most existing sorting methods, which typically only sort cells into two outlet channels.
Noninvasive cell trapping and patterning
A glass reflector with etched fluidic channels is clamped to the PCB holding the transducer. Cells infused into the chip are trapped in the ultrasonic standing wave formed in the channel. The acoustic forces focus the cells into clusters in the center of the channel as illustrated in the inset. Since the trapping occurs close to the transducer surface, the actual trapping sites are given by the near-field pressure distribution as shown in the 3D image. Cells will be trapped in clusters around the local pressure minima creating different patterns depending on the number of cells trapped. The peaks in the graph correspond to the pressure minima.
Manipulation of single cell, particle, or organism

Manipulating single cells is important to many biological studies, such as in controlling the cellular microenvironment and isolating specific cells of interest. Acoustic tweezers have been demonstrated to manipulate each individual cell with micrometer-level resolution. Cells generally have a diameter of 10–20 μm. To meet the resolution requirements of manipulating single cells, short-wavelength acoustic waves should be employed. In this case, a surface acoustic wave (SAW) is preferred to a bulk acoustic wave (BAW), because it allows using shorter-wavelength acoustic waves (normally less than 200 μm). Ding et al. reported a SSAW microdevice that is able to manipulate single cells with prescribed paths. Figure 6 records a demonstration that the movement of single cells can be finely controlled with acoustic tweezers. The working principle of the device lies in the controlled movement of pressure nodes in an SSAW field. Ding et al. employed chirped interdigital transducers (IDTs) that are able to generate SSAWs with adjustable positions of pressure nodes by changing the input frequency. They also showed that the millimeter-sized microorganism C. elegan can be manipulated in the same manner. They also examined cell metabolism and proliferation after acoustic treatment, and found no significant differences compared to the control group, indicating the non-invasive nature of acoustic base manipulation. In addition to using chirped IDTs, phaseshift-based single particle/cell manipulation has also been reported.
Manipulation of single biomolecules
Sitters et al. have shown that acoustics can be used to manipulate single biomolecules such as DNA and proteins. This method, which the inventors call acoustic force spectroscopy, allows measuring the force response of single molecules. This is achieved by attaching small microspheres to the molecules at one side and attaching them to a surface at the other. By pushing the microspheres away from the surface with a standing acoustic wave the molecules are effectively stretched out.
Manipulation of organic nano-materials
Polymer-dispersed liquid crystal (PDLC) displays can be switched from opaque to transparent using acoustic tweezers. A SAW-driven PDLC light shutter has been demonstrated by integrating a cured PDLC film and a pair of interdigital transducers (IDTs) onto a piezoelectric substrate.
Manipulation of inorganic nano-materials
Acoustic tweezers provide a simple approach for tuneable nanowire patterning. In this approach, SSAWs are generated by interdigital transducers, which induced a periodic alternating current (AC) electric field on the piezoelectric substrate and consequently patterned metallic nanowires in suspension. The patterns could be deposited onto the substrate after the liquid evaporated. By controlling the distribution of the SSAW field, metallic nanowires are assembled into different patterns including parallel and perpendicular arrays. The spacing of the nanowire arrays could be tuned by controlling the frequency of the surface acoustic waves.
Selective manipulation
While most acoustic tweezers are able to manipulate a large number of objects collectively, a complementary function is to be able to manipulate a single particle within a cluster without moving adjacent objects. To achieve this goal, the acoustic trap must be localized spacially. A first approach consists in using highly focused acoustic beams. Since many particles of interest are attracted to the nodes of an acoustic field and thus expelled from the focus point, some specific wave structures combining strong focalization but with a minimum of the pressure amplitude at the focal point (surrounded by a ring of intensity to create the trap) are required to trap this type of particle. These specific conditions are met by Bessel beams of topological order larger than zero, also called "acoustical vortices". With this kind of wave structures, the 2D and 3D selective manipulation of particles has been demonstrated with an array of transducers driven by programmable electronics.
Alternatively, another approach to localize the acoustic energy relies on the use of nanosecond-scale pulsed fields to generate localized acoustic standing waves.
High frequency tweezers and holographic InterDigitated Transducers (IDTs)
The individual selective manipulation of micro-objects requires to synthesize complex acoustic fields such as acoustic vortices (see previous section) at sufficiently high frequency to reach the necessary spatial resolution (typically the wavelength must be comparable to the size of the manipulated object to be selective). Many holographic methods have been developed to synthesize complex wavefields including transducer arrays, 3D printed holograms, metamaterials or diffraction gratings. Nevertheless, all these methods are limited to relatively low frequencies with an insufficient resolution to address micrometric particles, cells or microorganisms individually. On the other hand, InterDigitated Transducers (IDTs) were known as a reliable technique to synthesize acoustic wavefields up to GHz frequency.
See also
References
- Ozcelik, A., Rufo, J., Guo, F. et al. Acoustic tweezers for the life sciences. Nat Methods 15, 1021–1028 (2018). https://doi.org/10.1038/s41592-018-0222-9
- ^ Gorkov, L. P.; Soviet Physics- Doklady, 1962, 6(9), 773-775.
- ^ Nilsson, Andreas; Petersson, Filip; Jönsson, Henrik; Laurell, Thomas (2004). "Acoustic control of suspended particles in micro fluidic chips". Lab Chip. 4 (2). Royal Society of Chemistry (RSC): 131–135. doi:10.1039/b313493h. ISSN 1473-0197. PMID 15052353.
- Lin, Sz-Chin Steven; Mao, Xiaole; Huang, Tony Jun (2012). "Surface acoustic wave (SAW) acoustophoresis: now and beyond". Lab on a Chip. 12 (16). Royal Society of Chemistry (RSC): 2766–2770. doi:10.1039/c2lc90076a. ISSN 1473-0197. PMC 3992433. PMID 22781941.
- Ding, Xiaoyun; Li, Peng; Lin, Sz-Chin Steven; Stratton, Zackary S.; Nama, Nitesh; Guo, Feng; Slotcavage, Daniel; Mao, Xiaole; Shi, Jinjie; Costanzo, Francesco; Huang, Tony Jun (2013). "Surface acoustic wave microfluidics". Lab on a Chip. 13 (18). Royal Society of Chemistry (RSC): 3626–3649. doi:10.1039/c3lc50361e. ISSN 1473-0197. PMC 3992948. PMID 23900527.
- Dion, J. L.; Malutta, A.; Cielo, P. (1982). "Ultrasonic Inspection Of Fiber Suspensions". Journal of the Acoustical Society of America. 72 (5): 1524–1526. Bibcode:1982ASAJ...72.1524D. doi:10.1121/1.388688.
- King, Louis V. (1934-11-15). "On the acoustic radiation pressure on spheres". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 147 (861). The Royal Society: 212–240. Bibcode:1934RSPSA.147..212K. doi:10.1098/rspa.1934.0215. ISSN 2053-9169.
- Yosioka, K. and Kawasima, Y.; Acustica, 1955, 5(3), 167-173.
- ^ Bruus, Henrik (2012). "Acoustofluidics 7: The acoustic radiation force on small particles". Lab on a Chip. 12 (6). Royal Society of Chemistry (RSC): 1014–1021. doi:10.1039/c2lc21068a. ISSN 1473-0197. PMID 22349937.
- Weiser, M. A. H.; Apfel, R. E., and Neppiras, E. A.; Acustica, 1984, 56(2), 114-119.
- Laurell, Thomas; Petersson, Filip; Nilsson, Andreas (2007). "Chip integrated strategies for acoustic separation and manipulation of cells and particles". Chemical Society Reviews. 36 (3). Royal Society of Chemistry (RSC): 492–506. doi:10.1039/b601326k. ISSN 0306-0012. PMID 17325788.
- Doinikov, Alexander A. (1994). "Acoustic radiation pressure on a compressible sphere in a viscous fluid". Journal of Fluid Mechanics. 267: 1–22. Bibcode:1994JFM...267....1D. doi:10.1017/S0022112094001096. S2CID 123245307. Retrieved 10 April 2023.
- Baasch, Thierry; Pavlic, Alen; Dual, Jürg (December 2019). "Acoustic radiation force acting on a heavy particle in a standing wave can be dominated by the acoustic microstreaming". Phys. Rev. E. 100 (6): 061102. Bibcode:2019PhRvE.100f1102B. doi:10.1103/PhysRevE.100.061102. PMID 31962519. S2CID 210870075. Retrieved 10 April 2023.
- Lighthill, Sir James (1978). "Acoustic streaming". Journal of Sound and Vibration. 61 (3). Elsevier BV: 391–418. Bibcode:1978JSV....61..391L. doi:10.1016/0022-460x(78)90388-7. ISSN 0022-460X.
- Boluriann, S. and Morris, P. J.; Aeroacoustics, 2003, 2(3), 255-292.
- Bruus, Henrik (2012). "Acoustofluidics 2: Perturbation theory and ultrasound resonance modes". Lab Chip. 12 (1). Royal Society of Chemistry (RSC): 20–28. doi:10.1039/c1lc20770a. ISSN 1473-0197. PMID 22105715.
- Bruus, Henrik (15 December 2014). "Perturbation Theory and Ultrasound Resonances". Microscale Acoustofluidics. The Royal Society of Chemistry. pp. 29–45. doi:10.1039/9781849737067-00029. ISBN 978-1-84973-671-8.
- Petersson, Filip; Nilsson, Andreas; Holm, Cecilia; Jönsson, Henrik; Laurell, Thomas (2005). "Continuous separation of lipid particles from erythrocytes by means of laminar flow and acoustic standing wave forces". Lab Chip. 5 (1): 20–22. doi:10.1039/B405748C. ISSN 1473-0197. PMID 15616735.
- Shi, Jinjie; Huang, Hua; Stratton, Zak; Huang, Yiping; Huang, Tony Jun (2009). "Continuous particle separation in a microfluidic channel via standing surface acoustic waves (SSAW)". Lab on a Chip. 9 (23). Royal Society of Chemistry (RSC): 3354–3359. doi:10.1039/b915113c. ISSN 1473-0197. PMID 19904400.
- Nam, Jeonghun; Lim, Hyunjung; Kim, Dookon; Shin, Sehyun (2011). "Separation of platelets from whole blood using standing surface acoustic waves in a microchannel". Lab on a Chip. 11 (19). Royal Society of Chemistry (RSC): 3361–3364. doi:10.1039/c1lc20346k. ISSN 1473-0197. PMID 21842070.
- Ai, Ye; Sanders, Claire K.; Marrone, Babetta L. (2013-09-09). "Separation ofEscherichia coliBacteria from Peripheral Blood Mononuclear Cells Using Standing Surface Acoustic Waves". Analytical Chemistry. 85 (19). American Chemical Society (ACS): 9126–9134. doi:10.1021/ac4017715. ISSN 0003-2700. PMC 3789253. PMID 23968497.
- Nam, Jeonghun; Lim, Hyunjung; Kim, Choong; Yoon Kang, Ji; Shin, Sehyun (2012). "Density-dependent separation of encapsulated cells in a microfluidic channel by using a standing surface acoustic wave". Biomicrofluidics. 6 (2). AIP Publishing: 24120–2412010. doi:10.1063/1.4718719. ISSN 1932-1058. PMC 3365908. PMID 22670167.
- Shi, Jinjie; Mao, Xiaole; Ahmed, Daniel; Colletti, Ashley; Huang, Tony Jun (2008). "Focusing microparticles in a microfluidic channel with standing surface acoustic waves (SSAW)". Lab Chip. 8 (2). Royal Society of Chemistry (RSC): 221–223. doi:10.1039/b716321e. ISSN 1473-0197. PMID 18231658.
- Shi, Jinjie; Yazdi, Shahrzad; Steven Lin, Sz-Chin; Ding, Xiaoyun; Chiang, I-Kao; Sharp, Kendra; Huang, Tony Jun (2011). "Three-dimensional continuous particle focusing in a microfluidic channel via standing surface acoustic waves (SSAW)". Lab on a Chip. 11 (14). Royal Society of Chemistry (RSC): 2319–24. doi:10.1039/c1lc20042a. ISSN 1473-0197. PMC 3997299. PMID 21709881.
- Li, Sixing; Ding, Xiaoyun; Guo, Feng; Chen, Yuchao; Lapsley, Michael Ian; et al. (2013-05-23). "An On-Chip, Multichannel Droplet Sorter Using Standing Surface Acoustic Waves". Analytical Chemistry. 85 (11). American Chemical Society (ACS): 5468–5474. doi:10.1021/ac400548d. ISSN 0003-2700. PMC 3988909. PMID 23647057.
- Ding, Xiaoyun; Lin, Sz-Chin Steven; Lapsley, Michael Ian; Li, Sixing; Guo, Xiang; Chan, Chung Yu; Chiang, I-Kao; Wang, Lin; McCoy, J. Philip; Huang, Tony Jun (2012). "Standing surface acoustic wave (SSAW) based multichannel cell sorting". Lab on a Chip. 12 (21). Royal Society of Chemistry (RSC): 4228–31. doi:10.1039/c2lc40751e. ISSN 1473-0197. PMC 3956451. PMID 22992833.
- ^ Gedge, Michael; Hill, Martyn (2012). "Acoustofluidics 17: Theory and applications of surface acoustic wave devices for particle manipulation" (PDF). Lab on a Chip. 12 (17). Royal Society of Chemistry (RSC): 2998–3007. doi:10.1039/c2lc40565b. ISSN 1473-0197. PMID 22842855.
- Ding, X.; Lin, S.-C. S.; Kiraly, B.; Yue, H.; Li, S.; Chiang, I.-K.; Shi, J.; Benkovic, S. J.; Huang, T. J. (2012-06-25). "On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves". Proceedings of the National Academy of Sciences. 109 (28): 11105–11109. Bibcode:2012PNAS..10911105D. doi:10.1073/pnas.1209288109. ISSN 0027-8424. PMC 3396524. PMID 22733731.
- Courtney, Charles R. P.; Demore, Christine E. M.; Wu, Hongxiao; Grinenko, Alon; Wilcox, Paul D.; Cochran, Sandy; Drinkwater, Bruce W. (2014-04-14). "Independent trapping and manipulation of microparticles using dexterous acoustic tweezers". Applied Physics Letters. 104 (15). AIP Publishing: 154103. Bibcode:2014ApPhL.104o4103C. doi:10.1063/1.4870489. ISSN 0003-6951.
- Meng, Long; Cai, Feiyan; Chen, Juanjuan; Niu, Lili; Li, Yanming; Wu, Junru; Zheng, Hairong (2012-04-23). "Precise and programmable manipulation of microbubbles by two-dimensional standing surface acoustic waves". Applied Physics Letters. 100 (17). AIP Publishing: 173701. Bibcode:2012ApPhL.100q3701M. doi:10.1063/1.4704922. ISSN 0003-6951.
- Wood, C. D.; Cunningham, J. E.; O'Rorke, R.; Wälti, C.; Linfield, E. H.; Davies, A. G.; Evans, S. D. (2009-02-02). "Formation and manipulation of two-dimensional arrays of micron-scale particles in microfluidic systems by surface acoustic waves". Applied Physics Letters. 94 (5). AIP Publishing: 054101. Bibcode:2009ApPhL..94e4101W. doi:10.1063/1.3076127. ISSN 0003-6951.
- Sitters, Gerrit; Kamsma, Douwe; Thalhammer, Gregor; Ritsch-Marte, Monika; Peterman, Erwin J G; Wuite, Gijs J L (2014-11-24). "Acoustic force spectroscopy". Nature Methods. 12 (1). Springer Science and Business Media LLC: 47–50. doi:10.1038/nmeth.3183. ISSN 1548-7091. PMID 25419961. S2CID 12886472.
- Liu, Yan Jun; Ding, Xiaoyun; Lin, Sz-Chin Steven; Shi, Jinjie; Chiang, I-Kao; Huang, Tony Jun (2011-03-14). "Surface Acoustic Wave Driven Light Shutters Using Polymer-Dispersed Liquid Crystals". Advanced Materials. 23 (14). Wiley: 1656–1659. Bibcode:2011AdM....23.1656L. doi:10.1002/adma.201003708. ISSN 0935-9648. PMID 21438028. S2CID 205238981.
- Chen, Yuchao; Ding, Xiaoyun; Steven Lin, Sz-Chin; Yang, Shikuan; Huang, Po-Hsun; et al. (2013-04-09). "Tunable Nanowire Patterning Using Standing Surface Acoustic Waves". ACS Nano. 7 (4). American Chemical Society (ACS): 3306–3314. doi:10.1021/nn4000034. ISSN 1936-0851. PMC 3989880. PMID 23540330.
- Lee, Jungwoo; Teh, Shia-Yen; Lee, Abraham; Kim, Hyung Ham; Lee, Changyang; Shung, K. Kirk (2009-08-17). "Single beam acoustic trapping". Applied Physics Letters. 95 (7). AIP Publishing: 073701. Bibcode:2009ApPhL..95g3701L. doi:10.1063/1.3206910. ISSN 0003-6951. PMC 2755305. PMID 19798424.
- ^ Courtney, Charles R. P.; Demore, Christine E. M.; Wu, Hongxiao; Grinenko, Alon; Wilcox, Paul D.; Cochran, Sandy; Drinkwater, Bruce W. (2014-04-14). "Independent trapping and manipulation of microparticles using dexterous acoustic tweezers". Applied Physics Letters. 104 (15): 154103. Bibcode:2014ApPhL.104o4103C. doi:10.1063/1.4870489. ISSN 0003-6951.
- Baresch, Diego; Thomas, Jean-Louis; Marchiano, Régis (2016-01-11). "Observation of a Single-Beam Gradient Force Acoustical Trap for Elastic Particles: Acoustical Tweezers" (PDF). Physical Review Letters. 116 (2). American Physical Society (APS): 024301. Bibcode:2016PhRvL.116b4301B. doi:10.1103/physrevlett.116.024301. ISSN 0031-9007. PMID 26824541. S2CID 206267537.
- ^ Marzo, Asier; Seah, Sue Ann; Drinkwater, Bruce W.; Sahoo, Deepak Ranjan; Long, Benjamin; Subramanian, Sriram (2015-10-27). "Holographic acoustic elements for manipulation of levitated objects". Nature Communications. 6 (1): 8661. Bibcode:2015NatCo...6.8661M. doi:10.1038/ncomms9661. ISSN 2041-1723. PMC 4627579. PMID 26505138.
- Collins, David J.; Devendran, Citsabehsan; Ma, Zhichao; Ng, Jia Wei; Neild, Adrian; Ai, Ye (2016). "Acoustic tweezers via sub–time-of-flight regime surface acoustic waves". Science Advances. 2 (7). American Association for the Advancement of Science (AAAS): e1600089. Bibcode:2016SciA....2E0089C. doi:10.1126/sciadv.1600089. ISSN 2375-2548. PMC 4956186. PMID 27453940.
- Hefner, Brian T.; Marston, Philip L. (1999-11-23). "An acoustical helicoidal wave transducer with applications for the alignment of ultrasonic and underwater systems". The Journal of the Acoustical Society of America. 106 (6): 3313–3316. Bibcode:1999ASAJ..106.3313H. doi:10.1121/1.428184. ISSN 0001-4966.
- Thomas, Jean-Louis; Marchiano, Régis (2003-12-11). "Pseudo Angular Momentum and Topological Charge Conservation for Nonlinear Acoustical Vortices". Physical Review Letters. 91 (24): 244302. Bibcode:2003PhRvL..91x4302T. doi:10.1103/PhysRevLett.91.244302. PMID 14683126.
- Volke-Sepúlveda, Karen; Santillán, Arturo O.; Boullosa, Ricardo R. (2008-01-16). "Transfer of Angular Momentum to Matter from Acoustical Vortices in Free Space". Physical Review Letters. 100 (2): 024302. Bibcode:2008PhRvL.100b4302V. doi:10.1103/PhysRevLett.100.024302. PMID 18232874.
- Melde, Kai; Mark, Andrew G.; Qiu, Tian; Fischer, Peer (September 2016). "Holograms for acoustics". Nature. 537 (7621): 518–522. Bibcode:2016Natur.537..518M. doi:10.1038/nature19755. ISSN 1476-4687. PMID 27652563. S2CID 4403584.
- Jiang, Xue; Li, Yong; Liang, Bin; Cheng, Jian-chun; Zhang, Likun (2016-07-12). "Convert Acoustic Resonances to Orbital Angular Momentum". Physical Review Letters. 117 (3): 034301. Bibcode:2016PhRvL.117c4301J. doi:10.1103/PhysRevLett.117.034301. PMID 27472113.
- Jiménez, Noé; Picó, R.; Sánchez-Morcillo, V.; Romero-García, V.; García-Raffi, L. M.; Staliunas, K. (2016-11-23). "Formation of high-order acoustic Bessel beams by spiral diffraction gratings". Physical Review E. 94 (5): 053004. arXiv:1604.08353. Bibcode:2016PhRvE..94e3004J. doi:10.1103/PhysRevE.94.053004. hdl:2117/101154. PMID 27967159. S2CID 27190492.
- Jiménez, Noé; Romero-García, Vicent; García-Raffi, Luis M.; Camarena, Francisco; Staliunas, Kestutis (2018-05-14). "Sharp acoustic vortex focusing by Fresnel-spiral zone plates". Applied Physics Letters. 112 (20): 204101. Bibcode:2018ApPhL.112t4101J. doi:10.1063/1.5029424. hdl:2117/118785. ISSN 0003-6951.
- Yeo, Leslie Y.; Friend, James R. (2014-01-03). "Surface Acoustic Wave Microfluidics". Annual Review of Fluid Mechanics. 46 (1): 379–406. Bibcode:2014AnRFM..46..379Y. doi:10.1146/annurev-fluid-010313-141418. ISSN 0066-4189.
External links
- Fast acoustic tweezers—YouTube video illustrating how acoustic tweezers work
 , which is caused by the incoming acoustic waves and the scattering on the surface of the particle when acoustic waves propagate through it. For a compressible spherical particle with a diameter much smaller than the wavelength of acoustic waves in an ideal fluid, the acoustic radiation force can be calculated by
, which is caused by the incoming acoustic waves and the scattering on the surface of the particle when acoustic waves propagate through it. For a compressible spherical particle with a diameter much smaller than the wavelength of acoustic waves in an ideal fluid, the acoustic radiation force can be calculated by  is a given quantity, also called acoustic potential energy. The acoustic potential energy is expressed as:
is a given quantity, also called acoustic potential energy. The acoustic potential energy is expressed as:

 is the particle volume,
is the particle volume, is the acoustic pressure,
is the acoustic pressure, is the velocity of acoustic particles,
is the velocity of acoustic particles, is the fluid mass density,
is the fluid mass density, is the speed of sound of the fluid,
is the speed of sound of the fluid, is the time-average term,
is the time-average term, 
 and
and  can be calculated by
can be calculated by
 and
and 
 is the mass density of the particle,
is the mass density of the particle, is the speed of sound of the particle.
is the speed of sound of the particle. ,
,
 ,
,
 ,
,
 is the displacement of acoustic particle,
is the displacement of acoustic particle, is the acoustic pressure amplitude,
is the acoustic pressure amplitude, is the angular velocity,
is the angular velocity, is the wave number.
is the wave number. ,
,
 ,
,
 ,
,
 ,
,
 ,
,  ,
,
 is the acoustic energy density, and
is the acoustic energy density, and is
is  shows that the radiation force period is one-half of the pressure period. Also, the contrast factor can be positive or negative depending on the properties of particles and fluid. For positive value of
shows that the radiation force period is one-half of the pressure period. Also, the contrast factor can be positive or negative depending on the properties of particles and fluid. For positive value of 
 is the radius of the particle,
is the radius of the particle, is the distance between the particles,
is the distance between the particles, is the angle between the central line of the particles and the direction of propagation of the incident acoustic wave.
is the angle between the central line of the particles and the direction of propagation of the incident acoustic wave. and the right side depends on the acoustic pressure amplitude
and the right side depends on the acoustic pressure amplitude  . The velocity-dependent term is repulsive when particles are aligned with wave propagation (Θ=0°), and negative when perpendicular to wave propagation (Θ=90°). The pressure-dependent term is unaffected by the particle orientation and is always attractive. In the case of a positive contrast factor, the velocity-dependent term diminishes as particles are driven to the velocity node (pressure antinode), as in the case of air bubbles and lipid vesicles. In a similar way, the pressure-dependent term diminishes as particles are driven towards the pressure node (velocity antinode), as are most solid particles in aqueous solutions.
. The velocity-dependent term is repulsive when particles are aligned with wave propagation (Θ=0°), and negative when perpendicular to wave propagation (Θ=90°). The pressure-dependent term is unaffected by the particle orientation and is always attractive. In the case of a positive contrast factor, the velocity-dependent term diminishes as particles are driven to the velocity node (pressure antinode), as in the case of air bubbles and lipid vesicles. In a similar way, the pressure-dependent term diminishes as particles are driven towards the pressure node (velocity antinode), as are most solid particles in aqueous solutions.
 ,
,

 is the density of fluid,
is the density of fluid, is the velocity of fluid particle,
is the velocity of fluid particle, is the pressure,
is the pressure, is the dynamic viscosity of fluid,
is the dynamic viscosity of fluid, is the viscosity ratio.
is the viscosity ratio. ,
,  ,
,  , which are diminishing series with the higher-order terms much smaller than the lower-order ones.
, which are diminishing series with the higher-order terms much smaller than the lower-order ones.
 , the first-order equations can be obtained by collecting terms in first-order,
, the first-order equations can be obtained by collecting terms in first-order,
 ,
,
 .
.
 ,
,
 .
.
 .
.
 and
and  can be interpreted as the acoustic pressure and the velocity of the acoustic particle.
can be interpreted as the acoustic pressure and the velocity of the acoustic particle.
 and force source
and force source  . Generally, the acoustic streaming is a steady mean flow, where the response time scale is much smaller than the one of the acoustic vibration. The time-average term
. Generally, the acoustic streaming is a steady mean flow, where the response time scale is much smaller than the one of the acoustic vibration. The time-average term  is normally used to present the acoustic streaming. By using
is normally used to present the acoustic streaming. By using  , the time-average second-order equations can be obtained:
, the time-average second-order equations can be obtained:
 ,
,
 .
.
 ,
,
 .
.
 is the fluid velocity,
is the fluid velocity, is the velocity of particle.
is the velocity of particle.