Misplaced Pages

Adiabatic electron transfer

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Chemical reaction mechanism for redox reactions

In chemistry, adiabatic electron-transfer is a type of oxidation-reduction process. The mechanism is ubiquitous in nature in both the inorganic and biological spheres. Adiabatic electron-transfers proceed without making or breaking chemical bonds. Adiabatic electron-transfer can occur by either optical or thermal mechanisms. Electron transfer during a collision between an oxidant and a reductant occurs adiabatically on a continuous potential energy surface.

History

Noel Hush is often credited with formulation of the theory of adiabatic electron-transfer.

Fig. 1. Electron transfer occurs between donor (D) and acceptor (A) species separated by distance R that may be found in many forms in both condensed phases and the gas phase. Internal structure, external structure, or chance collisions provide interconnection between the species. Upon electron transfer, the structure of the local chemical environments involving D and A change, as does the polarization these species induce on any surrounding media.

Figure 1 sketches the basic elements of adiabatic electron-transfer theory. Two chemical species (ions, molecules, polymers, protein cofactors, etc.) labelled D (for “donor”) and A (for “acceptor”) become a distance R apart, either through collisions, covalent bonding, location in a material, protein or polymer structure, etc. A and D have different chemical environments. Each polarizes their surrounding condensed media. Electron-transfer theories describe the influence of a variety of parameters on the rate of electron-transfer. All electrochemical reactions occur by this mechanism. Adiabatic electron-transfer theory stresses that intricately coupled to such charge transfer is the ability of any D-A system to absorb or emit light. Hence fundamental understanding of any electrochemical process demands simultaneous understanding of the optical processes that the system can undergo.

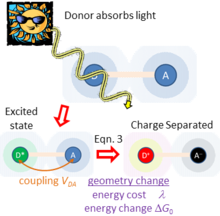
Fig. 2. When the donor species absorbs light energy, it goes into a high-energy excited state, generating significant changes to its local chemical environment and the polarization of its external environment. These environments facilitate coupling V D A {\displaystyle V_{DA}} between the donor and acceptor, which drives photochemical charge separation with a rate given by Eqn. (3) in the weak-coupling limit. This rate is also dependent on the energy λ {\displaystyle \lambda } required to rearrange the atoms to the preferred local geometry and environment polarization of the charge-separated state D-A and the energy change Δ G 0 {\displaystyle \Delta G_{0}} associated with charge separation.

Figure 2 sketches what happens if light is absorbed by just one of the chemical species, taken to be the charge donor. This produces an excited state of the donor. As the donor and acceptor are close to each other and surrounding matter, they experience a coupling V D A {\displaystyle V_{DA}} . If the free energy change Δ G 0 {\displaystyle \Delta G_{0}} is favorable, this coupling facilitates primary charge separation to produce D-A , producing charged species. In this way, solar energy is captured and converted to electrical energy. This process is typical of natural photosynthesis as well as modern organic photovoltaic and artificial photosynthesis solar-energy capture devices. The inverse of this process is also used to make organic light-emitting diodes (OLEDs).

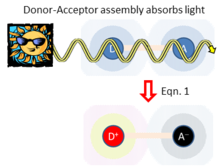
Fig. 3. Light energy is absorbed by the donor and acceptor, initiating intervalence charge transfer to directly convert solar energy into electrical energy as D-A. In the weak-coupling limit, the coupling V D A {\displaystyle V_{DA}} , reorganization energy λ {\displaystyle \lambda } , and the free energy change Δ G 0 {\displaystyle \Delta G_{0}} control the rate of light absorption (and hence charge separation) via Eqn. (1).

Adiabatic electron-transfer is also relevant to the area of solar energy harvesting. Here, light absorption directly leads to charge separation D-A. Hush's theory for this process considers the donor-acceptor coupling V D A {\displaystyle V_{DA}} , the energy λ {\displaystyle \lambda } required to rearrange the atoms from their initial geometry to the preferred local geometry and environment polarization of the charge-separated state, and the energy change Δ G 0 {\displaystyle \Delta G_{0}} associated with charge separation. In the weak-coupling limit ( 4 V D A 2 / λ 2 ≪ 1 {\displaystyle 4V_{DA}^{2}/\lambda ^{2}\ll 1} ), Hush showed that the rate of light absorption (and hence charge separation) is given from the Einstein equation by

k ∝ V D A 2 R 2 λ + Δ G 0 . {\displaystyle k\propto {\frac {V_{DA}^{2}R^{2}}{\lambda +\Delta G_{0}}}.} … (1)

This theory explained how Prussian blue absorbes light, creating the field of intervalence charge transfer spectroscopy.

Adiabatic electron transfer is also relevant to the Robin-Day classification system, which codifies types of mixed valence compounds. An iconic system for understanding Inner sphere electron transfer is the mixed-valence Creutz-Taube ion, wherein otherwise equivalent Ru(III) and Ru(II) are linked by a pyrazine. The coupling V D A {\displaystyle V_{DA}} is not small: charge is not localized on just one chemical species but is shared quantum mechanically between two Ru centers, presenting classically forbidden half-integral valence states. that the critical requirement for this phenomenon is

2 | J D A | λ ≥ 1. {\displaystyle {\frac {2|J_{DA}|}{\lambda }}\geq 1.} … (2)

Adiabatic electron-transfer theory stems from London's approach to charge-transfer and indeed general chemical reactions applied by Hush using parabolic potential-energy surfaces. Hush himself has carried out many theoretical and experimental studies of mixed valence complexes and long range electron transfer in biological systems. Hush's quantum-electronic adiabatic approach to electron transfer was unique; directly connecting with the Quantum Chemistry concepts of Mulliken, it forms the basis of all modern computational approaches to modeling electron transfer. Its essential feature is that electron transfer can never be regarded as an “instantaneous transition”; instead, the electron is partially transferred at all molecular geometries, with the extent of the transfer being a critical quantum descriptor of all thermal, tunneling, and spectroscopic processes. It also leads seamlessly to understanding electron-transfer transition-state spectroscopy pioneered by Zewail.

In adiabatic electron-transfer theory, the ratio 2 V D A / λ {\displaystyle 2V_{DA}/\lambda } is of central importance. In the very strong coupling limit when Eqn. (2) is satisfied, intrinsically quantum molecules like the Creutz-Taube ion result. Most intervalence spectroscopy occurs in the weak-coupling limit described by Eqn. (1), however. In both natural photosynthesis and in artificial solar-energy capture devices, 2 V D A / λ {\displaystyle 2V_{DA}/\lambda } is maximized by minimizing λ {\displaystyle \lambda } through use of large molecules like chlorophylls, pentacenes, and conjugated polymers. The coupling V D A {\displaystyle V_{DA}} can be controlled by controlling the distance R at which charge transfer occurs- the coupling typically decreases exponentially with distance. When electron transfer occurs during collisions of the D and A species, the coupling is typically large and the “adiabatic” limit applies in which rate constants are given by transition state theory. In biological applications, however, as well as some organic conductors and other device materials, R is externally constrained and so the coupling set at low or high values. In these situations, weak-coupling scenarios often become critical.

In the weak-coupling (“non-adiabatic”) limit, the activation energy for electron transfer is given by the expression derived independently by Kubo and Toyozawa and by Hush. Using adiabatic electron-transfer theory, in this limit Levich and Dogonadze then determined the electron-tunneling probability to express the rate constant for thermal reactions as

k = 2 π V D A 2 ℏ ( 4 π λ k β T ) 1 / 2 exp ⁡ − ( Δ G 0 + λ ) 2 4 λ k β T {\displaystyle k={\frac {2\pi V_{DA}^{2}}{\hbar (4\pi \lambda k_{\beta }T)^{1/2}}}\exp {\frac {-(\Delta G_{0}+\lambda )^{2}}{4\lambda k_{\beta }T}}} . … (3)

This approach is widely applicable to long-range ground-state intramolecular electron transfer, electron transfer in biology, and electron transfer in conducting materials. It also typically controls the rate of charge separation in the excited-state photochemical application described in Figure 2 and related problems.

Marcus showed that the activation energy in Eqn. (3) reduces to λ / 4 {\displaystyle \lambda /4} in the case of symmetric reactions with Δ G 0 = 0 {\displaystyle \Delta G_{0}=0} . In that work, he also derived the standard expression for the solvent contribution to the reorganization energy, making the theory more applicable to practical problems. Use of this solvation description (instead of the form that Hush originally proposed) in approaches spanning the adiabatic and non-adiabatic limits is often termed “Marcus-Hush Theory”. These and other contributions, including the widespread demonstration of the usefulness of Eqn. (3), led to the award of the 1992 Nobel Prize in Chemistry to Marcus.

Adiabatic electron-transfer theory is also widely applied in Molecular Electronics. In particular, this reconnects adiabatic electron-transfer theory with its roots in proton-transfer theory and hydrogen-atom transfer, leading back to London's theory of general chemical reactions.

References

  1. Piechota, Eric J.; Meyer, Gerald J. (2019). "Introduction to Electron Transfer: Theoretical Foundations and Pedagogical Examples". Journal of Chemical Education. 96 (11): 2450–2466. Bibcode:2019JChEd..96.2450P. doi:10.1021/acs.jchemed.9b00489. S2CID 208754569.
  2. ^ Hush, N. S. (1967). Intervalence-transfer absorption. II. Theoretical considerations and spectroscopic data. Progress in Inorganic Chemistry. Vol. 8. pp. 391–444. doi:10.1002/9780470166093.ch7. ISBN 9780470166093.
  3. "Fellows Details". Royal Society. Retrieved 18 September 2015.
  4. ^ Hush, N. S. (1961). "Adiabatic theory of outer sphere electron-transfer reactions in solution". Transactions of the Faraday Society. 57: 577. doi:10.1039/TF9615700557.
  5. Warman, J. M.; Haas, M. P. d.; Paddon-Row, M. N.; Cotsaris, E.; Hush, N. S.; Oevering, H.; Verhoeven, J. W. (1986). "Light-induced giant dipoles in simple model compounds for photosynthesis". Nature. 320 (6063): 615–616. Bibcode:1986Natur.320..615W. doi:10.1038/320615a0. S2CID 4346663.
  6. Nelsen, S. F.; Ismagilov, R. F.; Trieber, D. A. (1997). "Adiabatic Electron Transfer: Comparison of Modified Theory with Experiment" (PDF). Science. 278 (5339): 846–849. Bibcode:1997Sci...278..846N. doi:10.1126/science.278.5339.846. PMID 9346480.
  7. German, E. D. (1979). "Intramolecular intervalence charge transfer in bimolecular mixed-valence complexes of metals". Chemical Physics Letters. 64 (2): 295–298. Bibcode:1979CPL....64..295G. doi:10.1016/0009-2614(79)80516-3.
  8. Sun, D. L.; Rosokha, S. V.; Lindeman, S. V.; Kochi, J. K. (2003). "Intervalence (Charge-Resonance) Transitions in Organic Mixed-Valence Systems. Through-Space versus Through-Bond Electron Transfer between Bridged Aromatic (Redox) Centers". Journal of the American Chemical Society. 125 (51): 15950–15963. doi:10.1021/ja037867s. PMID 14677987.
  9. Nelsen, S. F.; Weaver, M. N.; Luo, Y.; Lockard, J. V.; Zink, J. I. (2006). "Use of the neighboring orbital model for analysis of electronic coupling in Class III intervalence compounds". Chemical Physics. 324 (1): 195–201. Bibcode:2006CP....324..195N. doi:10.1016/j.chemphys.2006.01.023.
  10. Rosokha, S. V.; Kochi, J. K. (2008). "Fresh Look at Electron-Transfer Mechanisms via the Donor/Acceptor Bindings in the Critical Encounter Complex". Accounts of Chemical Research. 41 (5): 641–653. doi:10.1021/ar700256a. PMID 18380446.
  11. Robin, M. B.; Day, P. (1967). Mixed Valence Chemistry-A Survey and Classification. Advances in Inorganic Chemistry and Radiochemistry. Vol. 10. pp. 247–422. doi:10.1016/S0065-2792(08)60179-X. ISBN 9780120236107.
  12. Day, P.; Hush, N. S.; Clark, R. J. H. (2008). "Mixed valence: origins and developments". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 366 (1862): 5–14. Bibcode:2008RSPTA.366....5D. doi:10.1098/rsta.2007.2135. PMID 17827130. S2CID 5912503.
  13. Hush, N. S. (1975). "Inequivalent XPS binding energies in symmetrical delocalized mixed-valence complexes". Chemical Physics. 10 (2–3): 361–366. Bibcode:1975CP.....10..361H. doi:10.1016/0301-0104(75)87049-2.
  14. ^ London, F. (1932). "On the theory of non-adiabatic chemical reactions". Quantum Chemistry. World Scientific Series in 20th Century Chemistry. Vol. 74. pp. 32–60. doi:10.1142/9789812795762_0003. ISBN 978-981-02-2771-5.
  15. ^ Hush, N. S. (1953). "Quantum-mechanical discussion of the gas phase formation of quinonedimethide monomers". Journal of Polymer Science. 11 (4): 289–298. Bibcode:1953JPoSc..11..289H. doi:10.1002/pol.1953.120110401.
  16. ^ Hush, N. S. (1958). "Adiabatic rate processes at electrodes". The Journal of Chemical Physics. 28 (5): 962–972. Bibcode:1958JChPh..28..962H. doi:10.1063/1.1744305.
  17. Kornyshev, A. A.; Tosi, M.; Ulstrup, J. (1997). Electron and Ion Transfer in Condensed Media. Singapore: World Scientific. ISBN 978-9810229290.
  18. ^ Kuznetsov, A.; Ulstrup, J. (1998). Electron Transfer in Chemistry and Biology: An introduction to the theory. Chichester: Wiley. ISBN 978-0-471-96749-1.
  19. ^ Devault, D. (1980). "Quantum mechanical tunnelling in biological systems". Quarterly Reviews of Biophysics. 13 (4): 387–564. doi:10.1017/S003358350000175X. PMID 7015406. S2CID 26771752.
  20. Cave, R. J.; Newton, M. D. (1996). "Generalization of the Mulliken-Hush treatment for the calculation of electron transfer matrix elements". Chemical Physics Letters. 249 (1–2): 15–19. Bibcode:1996CPL...249...15C. doi:10.1016/0009-2614(95)01310-5.
  21. Reimers, J. R.; Hush, N. S. (2017). "Relating transition-state spectroscopy to standard chemical spectroscopic processes". Chemical Physics Letters. 683: 467–477. Bibcode:2017CPL...683..467R. doi:10.1016/j.cplett.2017.04.070. hdl:10453/125251.
  22. Kubo, R.; Toyozawa, Y. (1955). "Application of the Method of Generating Function to Radiative and Non-Radiative Transitions of a Trapped Electron in a Crystal". Progress of Theoretical Physics. 13 (2): 160–182. Bibcode:1955PThPh..13..160K. doi:10.1143/PTP.13.160.
  23. Levich, V. G.; Dogonadze, R. R. (1960). "Adiabatic theory for electron-transfer processes in solution". Proc. Akad. Naukl. SSSR. 133: 591.
  24. Levich, V. G.; Dogonadze, R. R. (1959). "Theory of rediationless electron transitions between ions in solution". Proc. Akad. Naukl. SSSR. 29: 9.
  25. Marcus, R. A. (1956). "On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. 1" (PDF). The Journal of Chemical Physics. 24 (5): 966–978. Bibcode:1956JChPh..24..966M. doi:10.1063/1.1742723. S2CID 16579694.
  26. Schmickler, W. Electron transfer and single molecule events (PDF). Paris: Eolss Publishers.
  27. Efrima, S.; Bixon, M. (1976). "Vibrational effects in outer-sphere electron-transfer reactions in polar media". Chemical Physics. 13 (4): 447–460. Bibcode:1976CP.....13..447E. doi:10.1016/0301-0104(76)87014-0.
  28. Marcus, R. A.; Sutin, N. (1985). "Electron transfers in chemistry and biology". Biochimica et Biophysica Acta (BBA) - Reviews on Bioenergetics. 811 (3): 265–322. doi:10.1016/0304-4173(85)90014-x.
  29. Reimers, J. R.; McKemmish, L.; McKenzie, R. H.; Hush, N. S. (2015). "A unified diabatic description for electron transfer reactions, isomerization reactions, proton transfer reactions, and aromaticity". Physical Chemistry Chemical Physics. 17 (38): 24598–24617. Bibcode:2015PCCP...1724598R. doi:10.1039/C5CP02236C. PMID 26193994.
  30. Horiuti, J.; Polanyi, M. (2003). "Outlines of a theory of proton transfer". Journal of Molecular Catalysis A: Chemical. 199 (1–2): 185–197. doi:10.1016/s1381-1169(03)00034-7.
Categories: