Misplaced Pages

This is a worked-through example showing the use of the analytic hierarchy process (AHP) in a practical decision situation.

See Analytic hierarchy process#Practical examples for context for this example.

Overview

This example describes the use of the AHP in choosing a leader for a company whose founder is about to retire. There are several competing candidates and several competing criteria for choosing the most suitable one. By using the AHP, the board of directors is able to choose the best candidate in a rational, transparent way that can be examined and understood by all concerned.

The diagram below shows the AHP hierarchy at the end of the decision-making process. The goal is to choose the most suitable leader based on four specific criteria. Dick is the preferred alternative, with a priority of .493. He is preferred about a third more strongly than Tom, whose priority is .358, and about three times more strongly than Harry, whose priority is only .149. Experience is the most important criterion with respect to reaching the goal, followed by Charisma, Education, and Age. These factors are weighted .547, .270, .127, and .056, respectively.

The balance of this article describes the derivation of these priorities.

Example details

Decision scenario

The company, founded in 1960, makes specialized industrial equipment. Its future success will depend on maintaining the strength of its older product lines and on generating a constant flow of new ones. The company's founder is retiring soon, and a consulting firm has developed a detailed plan for continuing its success in his absence. The plan will take five years to implement, and will replace the founder's highly subjective "seat of the pants" style with a more carefully thought out way of doing business.

The board of directors needs to choose someone to lead the company through the change and upheaval that implementing the consultant's plan will involve. In doing this work, the new leader will be required to make many unpopular decisions and take many unpopular actions. He or she will be expected to “clear the air” by stepping aside after the plan is fully implemented.

Six months ago, the board said:

After much thought and discussion, we have identified four criteria to be used in choosing the person to guide us through the upcoming period of change: experience, education, charisma and age. Experience is important because the job requires skills and knowledge that can only be developed through practical application. And though our beloved founder was a self-made man who didn’t finish high school, the times demand that our new leader have an appropriate university education. Since the new leader will have to keep us all motivated during a difficult period of change, we prefer someone with an active, charismatic leadership style. Finally, the new leader's Age is important because he or she will need to have an appropriate career path after stepping down five years from now. — Board of directors, letter to employees and shareholders

Last week, they said:

After an extensive search, we have selected three candidates for this very challenging position. All are presently executives with the company. Choosing among them will be difficult, but we plan to announce our decision shortly. — Board of directors, followup letter to employees and shareholders

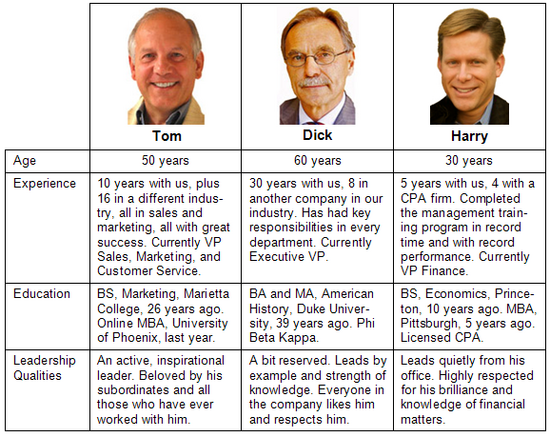
The three candidates are Tom, Dick, and Harry. Summaries of their backgrounds are shown below:

Decision hierarchy

The AHP hierarchy for this decision is shown below.

As the decision makers continue with the AHP, they will determine priorities for the candidates with respect to each of the decision criteria, and priorities for each of the criteria with respect to their importance in reaching the goal.

The priorities will then be combined throughout the hierarchy to give an overall priority for each candidate. The candidate with the highest priority will be the most suitable Alternative, and the ratios of the candidates' priorities will indicate their relative strengths with respect to the Goal.

Pairwise comparisons

The priorities will be derived from a series of measurements: pairwise comparisons involving all the nodes.

Each colored box in the hierarchy diagram above is called a node.

The nodes at each level will be compared, two by two, with respect to their contribution to the nodes above them. The results of these comparisons will be entered into a matrix which is processed mathematically to derive the priorities for all the nodes on the level.

The comparisons can be made in any sequence, but in this example we will begin by comparing the Alternatives with respect to their strengths in meeting each of the Criteria. Then we'll compare the Criteria with respect to their importance to reaching the Goal.

Since there are three alternatives (Tom, Dick, and Harry) and we need to compare each one to each of the others, the decision makers (the Board) will make three pairwise comparisons with respect to each Criterion: Tom vs. Dick, Tom vs. Harry, and Dick vs. Harry. For each comparison, the Board will first judge which member of the pair is weaker with respect to the Criterion under consideration. Then they will assign a relative weight to the other candidate.

They will use the AHP fundamental scale in assigning the weights:

Alternatives vs. criteria

Experience

Using their knowledge of the work the leaders will be required to do, the board needs to evaluate the candidates' strengths with respect to experience. Though they have good information about each candidate's work history, there is no such thing as an objective scale for measuring "experience." Thanks to the AHP, the Board will be able to develop a scale, applying only to this one case, that measures the candidates' relative strengths with respect to experience.

Here is the Board's thinking about experience:

The leader will implement a wide-ranging plan that involves major changes to a successful business. This work requires skills, knowledge, wisdom, and judgment that are usually present only in seasoned executives. Furthermore, the company is so complex and specialized that only direct experience inside it can equip a prospective leader for his job. Outside experience is also important, since it provides perspective and a view of the larger picture. — Board of Directors, Internal Memorandum

As a reminder, here is their summary of the candidates' experience:

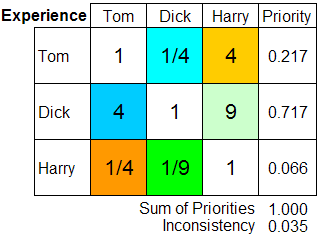
The next step in the AHP is to compare pairs of candidates with respect to Experience. For each comparison, the Board decides which candidate is the weaker with respect to Experience, giving his experience a weight of 1. Then, using the AHP Fundamental Scale, they assign a weight to the experience of the other candidate.

Their comparisons are summarized below. (A summary in this form is not an essential part of the AHP. It is presented here only to help readers understand this example. The colors in the squares will help them see where each entry belongs in the AHP matrix):

The next step is to transfer the weights to a matrix, using a method unique to the AHP. For each pairwise comparison, the number representing the greater weight is transferred to the box of the corresponding color; the reciprocal of that number is put into the box of the color corresponding to the smaller number:

By processing this matrix mathematically, the AHP derives priorities for the candidates with respect to Experience. The priorities are measurements of their relative strengths, derived from the judgments of the decision makers as entered into the matrix. Mathematically speaking, they are the values in the matrix's principal right eigenvector. These values can be calculated in many ways, including by hand, or with a spreadsheet program, or by using specialized AHP software. They are shown below to the right of the matrix, along with an Inconsistency Factor computed by the specialized AHP software that was used to process the data:

Education

Now the Board needs to evaluate the candidates with respect to Education. Here is their thinking on the subject:

The leader needs to have a good education, preferably with a recent MBA or engineering degree. Our founder is a self-made man who didn’t finish high school. He created a successful company that relies strongly on his personal insights and “seat-of-the pants” judgment. But when he retires and we move into a more complex future, we need to become more thoughtfully run. Having an educated leader is vitally important to this. Education is also important because our employees, particularly the technical staff, are hungry to have it in their leader. Though they love and respect “the Old Man,” they have often been frustrated by his lack of appreciation for today's tools of business, engineering, and manufacturing. — Board of Directors, Internal Memorandum

Though a person's education can be measured by academic degrees, grades and honors, those measurements are not so useful in this non-academic situation. Through its system of pairwise comparisons, the AHP can develop accurate measurements that are perfectly suited to the decision at hand. Here is the Board's summary of the candidates' educational backgrounds:

As they did previously with Experience, the Board now compares pairs of candidates with respect to Education. For each comparison, the Board decides which candidate is the weaker with respect to Education, giving his education a weight of 1. Then, using the AHP Fundamental Scale, they assign a weight to the education of the other candidate. For the sake of our example, we again provide a table summarizing their deliberations:

The Board transcribes its judgments into the AHP matrix shown below. Looking at Tom's row in the matrix, we can see that his education has three times the weight of Dick's, but only a fifth the weight of Harry's. Similar relationships can be seen in the other two rows, where Dick's education is strongly dominated by Tom's and Harry's, while Harry's education strongly dominates that of both the other men.

Once again we use AHP software to derive priorities from the numbers in the AHP matrix:

The priorities tell us that, according to the judgment of the decision makers, Harry's education is by far the strongest of the three. Generally speaking, it dominates Tom's by a factor of almost 4, (0.731÷0.188=3.95) and Dick's by a factor of 9 (0.731÷0.081=9.02).

Charisma

The Board's next step is to pairwise compare the Alternatives (candidates) with respect to Charisma. Here's what they have to say about it:

As implementation of the plan proceeds, the leader will need to overcome people’s natural resistance to change. We think he will often need to wield influence on the basis of his personal charm and appeal, rather than on talk, logic, or authority alone. We have called this charm and appeal “charisma”. It will be an important factor in the leader’s ability to implement the plan. — Board of Directors, Internal Memorandum

Here is their summary of the candidates' leadership qualities:

And here are their judgments about those qualities as they relate to Charisma:

Putting their judgments into the matrix and processing it with the AHP software, they get:

Note that even though "charisma" is a highly subjective concept with no imaginable measurement scale, the AHP has allowed the board to measure its relative strength among these three candidates. Also note that with different candidates, or even with different board members, the measurements would likely be different as well. The AHP's measurements apply only to the specific case at hand.

Age

A person's age can be determined with a precision of days or even minutes. But such measurements aren't highly useful in making the decision at hand, since there is more to "Age" in this context than mere chronology.

Also, there are U.S. laws against employment discrimination by age. Anyone using age as a decision factor must be very explicit about their reasons and justifications. In this case, it wouldn't be good if an unsuccessful candidate decided to sue the company on the basis of age discrimination.

The Board has said this about Age:

The leader will be expected to step down five years from now. For his benefit and ours, we need to consider how old he will be at that time. If he is at or near retirement age, he can just retire, possibly remaining with us in a consulting capacity. If he is younger, he will have more years to work, but there will likely be no place for him in our company. Based on his success as our leader, he might or might not be easily employable elsewhere. He could possibly join a competitor and take key people with him, in spite of any non-compete agreements we might negotiate. The leader's age also affects his ability to interact with our workforce. Many of the people involved with our important legacy products are over age 55. Most of those connected with our newer products are in their 20s and 30s. It is important that the leader is able to relate to both these age groups, and that they are able to accept his leadership. — Board of Directors, Internal Memorandum

Tom, Dick, and Harry are now 50, 60, and 30 years old respectively. Here's a summary of the Board's evaluation of them with respect to Age:

Transferring their judgments to an AHP matrix and processing it with software yields this result for the Alternatives with respect to Age:

Criteria vs. the Goal

Now that the decision makers have evaluated the Alternatives (candidates) with respect to their strength in meeting the Criteria, they need to evaluate the Criteria with respect to their importance in reaching the goal.

Once again they do this by a series of pairwise comparisons. As with the Alternatives, this part of the process requires much discussion and debate among the decision makers.

In this case, the Board agrees on these relative weights for the various pairs of Criteria:

Note that pairwise comparison of four nodes requires six separate comparisons, while that of three nodes requires only three.

These comparisons require a larger matrix, but it is processed in the same way as the smaller ones. Here is the matrix for the Criteria, along with the resulting priorities and Consistency Factor:

Note that, in this decision, Experience, the highest ranked Criterion, is about twice as important in reaching the goal as the second-highest ranked Criterion, Charisma. Similarly, Charisma is about twice as important as Education, which in turn is more than twice as important as Age.

Synthesizing final priorities

Now that we know the priorities of the Criteria with respect to the Goal, and the priorities of the Alternatives with respect to the Criteria, we can calculate the priorities of the Alternatives with respect to the Goal. This is a straightforward matter of multiplying and adding, carried out over the whole of the hierarchy.

In our example, each Alternative's priority with respect to reaching the Goal is the sum of:

• His priority with respect to Experience, multiplied by Experience's priority with respect to the Goal, and
• His priority with respect to Education, multiplied by Education's priority with respect to the Goal, and
• His priority with respect to Charisma, multiplied by Charisma's priority with respect to the Goal, and
• His priority with respect to Age, multiplied by Age's priority with respect to the Goal

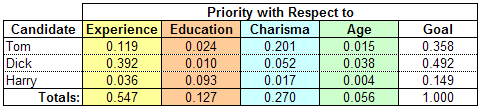
Here are the calculations for the Candidates with respect to the Criteria:

Looking only at Tom, we can see that his priority with respect to the Goal is 0.358, calculated as follows:

• Tom's priority with respect to Experience is 0.217 x 0.547 = 0.119, plus
• Tom's priority with respect to Education is 0.188 x 0.127 = 0.024, plus
• Tom's priority with respect to Charisma is 0.703 x 0.270 = 0.201, plus
• Tom's priority with respect to Age is 0.265 * 0.056 = 0.015,
• For a total of 0.119 + 0.024 + 0.201 + 0.015 = 0.358

Here are the overall priorities for all of the Candidates:

Making the decision

Based on the Board's choice of decision criteria, on their judgments about the relative importance of each, and on their judgments about each candidate with respect to each of the criteria, Dick, with a priority of 0.492, is by far the most suitable candidate. Tom, with a priority of 0.358, is second, and Harry, at 0.149, is third.

The Board should choose Dick as the company's new leader.

Because they have used the AHP, it is easy for them to trace their thinking and to justify the steps along the way to their decision. If they have second thoughts about the outcome, they can revisit the process and make changes if appropriate. And if they choose to, they can reveal the details of their process to their consultants and confidants, to the candidates, to the shareholders, or to anyone else who might be concerned with the decision.

References

Notes

1. The form and content of the hierarchy are dependent on the wants and needs of the decision makers. If the consultant's plan, for example, included moving all manufacturing to China, the board may well have added Chinese Language Skills as one of its Criteria. Also for example, if they had wanted to do so at any point in the process, they could have included Technical Education and Business Education as Subcriteria under Education, or made any other changes that they thought would be helpful in their deliberations.
2. The priorities on any level add up to 1.000, and they represent relative levels of strength or importance. If the priorities of the Criteria were Education=0.500, Experience=0.250, and Charisma and Age each=0.125, then Education would be twice as important as Experience in reaching the Goal, and four times as important as either Charisma or Age. Experience would be half as important as Education and twice as important as Charisma and Age. The actual priorities, of course, depend on the judgments input by the decision makers.
3. The mathematics underlying the AHP has been presented in many books and papers since the 1980s. A technical discussion of the subject is beyond the scope of this article, but a basic explanation for decision makers appears in Saaty (2008), Chapter 5. A much more detailed exposition is in Saaty (2006), Chapters 1 - 3.
4. For one-time decisions like this one, experienced AHP practitioners commonly work from the bottom up, first evaluating the Alternatives with respect to the Criteria, then evaluating the Criteria with respect to the Goal. Where the decision is a repetitive one, they commonly work from the top down.
5. A detailed description of the AHP matrix, including what numbers should go into which cells and why they should go there, can be found in Saaty (2008), Chapter 5. For this example, just follow the colors and everything will end up in the right place.
6. This example uses the Superdecisions AHP software throughout. Like most AHP software, it calculates an Inconsistency Factor, which is a measure of the internal consistency of the judgments entered into the matrix. It is desirable that this factor be less than 0.100. The Inconsistency Factor is further discussed in Saaty (2006), Chapter 2, especially on page 61.
7. An important aspect of the AHP is that it forces the decision makers to look closely at every aspect of the decision.
8. The number of comparisons increases very rapidly with the number of nodes compared. If C is the number of comparisons required and N is the number of nodes to be compared, C = N x (N-1)/2. The practical limit on nodes that can be compared is about eight (requiring 8 x 7 / 2 = 28 comparisons). There are other reasons to keep the number of compared nodes below ten: Psychological studies show that the number of items that can be successfully held in mind for activities like this is between five and nine, and some of the math on which the AHP is based is most dependable in this range (see The Magical Number Seven, Plus or Minus Two; Saaty (2006) p. 61; and Saaty (2010), p. 109).
9. In our example, we can easily make these calculations by hand or in a spreadsheet. It can be impractical to do this in real world cases with much larger hierarchies: it's tedious to make so many calculations, and it's easy to introduce errors. Specialized AHP software programs make these calculations automatically and with a high degree of accuracy.
10. Most AHP software includes features to help in reviewing decisions. One common "what if?" feature is Sensitivity Analysis. This provides an easy way to see, usually graphically, what would happen to the final priorities if a given criterion were given a different weight. The Superdecisions software used in this example revealed that moderate changes in the weight of any criterion would have little effect on the final decision.

Bibliography

The Tom, Dick, and Harry example draws heavily on principles described in the books below, which are the current basic texts on the AHP. They contain detailed descriptions of the theory underlying the process, plus many examples of its use in the real world.

• Saaty, Thomas L. (2006). Fundamentals of Decision Making and Priority Theory. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-6-3.
• Saaty, Thomas L. (2008). Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-8-X.
• Saaty, Thomas L. (2010). Principia Mathematica Decernendi: Mathematical Principles of Decision Making. Pittsburgh, Pennsylvania: RWS Publications. ISBN 978-1-888603-10-1.

External links

• AHPy - AHPy provides a worked example of a slight variant of this problem in its README

• Group decision-making