| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Arrhenius plot" – news · newspapers · books · scholar · JSTOR (October 2023) (Learn how and when to remove this message) |
In chemical kinetics, an Arrhenius plot displays the logarithm of a reaction rate constant, (, ordinate axis) plotted against reciprocal of the temperature (, abscissa). Arrhenius plots are often used to analyze the effect of temperature on the rates of chemical reactions. For a single rate-limited thermally activated process, an Arrhenius plot gives a straight line, from which the activation energy and the pre-exponential factor can both be determined.
The Arrhenius equation can be given in the form: where:
- = rate constant
- = pre-exponential factor
- = (molar) activation energy
- = gas constant, (, where is the Avogadro constant).
- = activation energy (for a single reaction event)
- = Boltzmann constant
- = absolute temperature
The only difference between the two forms of the expression is the quantity used for the activation energy: the former would have the unit joule/mole, which is common in chemistry, while the latter would have the unit joule and would be for one molecular reaction event, which is common in physics. The different units are accounted for in using either the gas constant or the Boltzmann constant .
Taking the natural logarithm of the former equation gives:
When plotted in the manner described above, the value of the y-intercept (at ) will correspond to , and the slope of the line will be equal to . The values of y-intercept and slope can be determined from the experimental points using simple linear regression with a spreadsheet.
The pre-exponential factor, , is an empirical constant of proportionality which has been estimated by various theories which take into account factors such as the frequency of collision between reacting particles, their relative orientation, and the entropy of activation.
The expression represents the fraction of the molecules present in a gas which have energies equal to or in excess of activation energy at a particular temperature. In almost all practical cases, , so that this fraction is very small and increases rapidly with . In consequence, the reaction rate constant increases rapidly with temperature , as shown in the direct plot of against . (Mathematically, at very high temperatures so that , would level off and approach as a limit, but this case does not occur under practical conditions.)
Worked example
Considering as example the decomposition of nitrogen dioxide into nitrogen monoxide and molecular oxygen:
- 2 NO2 → 2 NO + O2
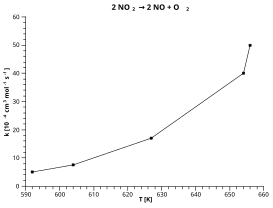 Direct plot: k against T
Direct plot: k against T Arrhenius plot: ln(k) against 1/T.
Arrhenius plot: ln(k) against 1/T.
Based on the red "line of best fit" plotted in the graph given above:
Let y = ln(k ) Let x = 1/TPoints read from graph:
y = 4.1 at x = 0.0015 y = 2.2 at x = 0.00165Slope of red line = (4.1 − 2.2) / (0.0015 − 0.00165) = −12,667
Intercept of red line = 4.1 + (0.0015 × 12667) = 23.1
Inserting these values into the form above: yields:

as shown in the plot at the right.
for:
- k in 10 cm mol s
- T in K
Substituting for the quotient in the exponent of : where the approximate value for R is 8.31446 J K mol
The activation energy of this reaction from these data is then:
Ea = R × 12,667 K = 105,300 J mol = 105.3 kJ mol.See also
References
- "6.2.3.4: The Arrhenius Law – Arrhenius Plots". Chemistry LibreTexts. 2013-10-02. Retrieved 2023-10-14.
 ,
,  ,
,  where:
where:
 =
=  =
=  = (molar)
= (molar)  =
=  , where
, where  is the
is the  =
=  =
=  =
= 
 ) will correspond to
) will correspond to  , and the
, and the  . The values of y-intercept and slope can be determined from the experimental points using
. The values of y-intercept and slope can be determined from the experimental points using  represents the fraction of the molecules present in a gas which have energies equal to or in excess of activation energy at a particular temperature. In almost all practical cases,
represents the fraction of the molecules present in a gas which have energies equal to or in excess of activation energy at a particular temperature. In almost all practical cases,  , so that this fraction is very small and increases rapidly with
, so that this fraction is very small and increases rapidly with  ,
,  yields:
yields:


 for:
for:
 :
:
 where the approximate value for
where the approximate value for