Misplaced Pages

Athermalization

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Process of achieving optothermal stability in optomechanical systems

Athermalization, in the field of optics, is the process of achieving optothermal stability in optomechanical systems. This is done by minimizing variations in optical performance over a range of temperatures.

Optomechanical systems are typically made of several materials with different thermal properties. These materials compose the optics (refractive or reflective elements) and the mechanics (optical mounts and system housing). As the temperature of these materials change, the volume and index of refraction will change as well, increasing strain and aberration content (primarily defocus). Compensating for optical variations over a temperature range is known as athermalizing a system in optical engineering.

Geometric ray trace (transmitting and refracting) of a positive Schott N-BK7 singlet (single glass type lens element) at 22 C. Red rays are from the 0 degree Y-field angle and blue rays are from the 2 degree Y-field angle.

Material property changes

Image generated in MATLAB by geometric ray tracing 1E6 rays through a positive N-BK7 singlet at a 2 degree Y-field angle. Singlet is in an aluminum 6061 housing cycled from -30 C to 70 C. Change in spot size and position is from variations in extensive and intensive properties as a function of temperature.

Thermal expansion is the driving phenomena for the extensive and intensive property changes in an optomechanical system.

Extensive properties

Extensive property changes, such as volume, alter the shape of optical and mechanical components. Systems are geometrically optimized for optical performance and are sensitive to components changing shape and orientation. While volume is a three dimensional parameter, thermal changes can be modeled in a single dimension with linear expansion, assuming an adequately small temperature range. For examples, glass manufacturer Schott provides the coefficient of linear thermal expansion for a temperature range of -30 C to 70 C. The change in length of a material is a function of the change in temperature with respect to the standard measurement temperature, T 0 {\textstyle T_{0}} . This temperature is typically room temperature or 22 degrees Celsius.

Δ T = T − T 0 {\displaystyle \Delta T=T-T_{0}\,}
L ( T ) = L 0 + Δ L = ( 1 + α Δ T ) L 0 {\displaystyle L_{\left(T\right)}=L_{0}+\Delta L=\left(1+\alpha \Delta T\right)L_{0}\,}

Where L ( T ) {\textstyle L_{\left(T\right)}} is the length of a material at temperature T {\textstyle T} , L 0 {\textstyle L_{0}} is the length of the material at temperature T 0 {\textstyle T_{0}} , Δ T {\textstyle \Delta T} is the change in temperature, and α {\textstyle \alpha } is the coefficient of thermal expansion. These equations describe how diameter, thickness, radius of curvature, and element spacing change as a function of temperature.

Intensive properties

Dispersion of N-BK7 over the visible spectrum using coefficients from the Schott Optical Glass Data Sheets.

The dominant intensive property change, in terms of optical performance, is the index of refraction. The refractive index of glass is a function of wavelength and temperature. There are multiple formulas that can be used to define the wavelength dependence, or dispersion, of a glass. Following the notation from Schott, the empirical Sellmeier equation is shown below.

n ( λ ,   T 0 ) = 1 + B 1 λ 2 λ 2 − C 1 + B 2 λ 2 λ 2 − C 2 + B 3 λ 2 λ 2 − C 3 {\displaystyle n_{\left(\lambda ,\ T_{0}\right)}={\sqrt {1+{\frac {B_{1}\lambda ^{2}}{\lambda ^{2}-C_{1}}}+{\frac {B_{2}\lambda ^{2}}{\lambda ^{2}-C_{2}}}+{\frac {B_{3}\lambda ^{2}}{\lambda ^{2}-C_{3}}}}}\,}
Temperature coefficients of the absolute refractive index of N-BK7 for the d, F, C spectrum.

Where λ {\textstyle \lambda } is wavelength and B 1 {\textstyle B_{1}} , B 2 {\textstyle B_{2}} , B 3 {\textstyle B_{3}} , C 1 {\textstyle C_{1}} , C 2 {\textstyle C_{2}} , and C 3 {\textstyle C_{3}} are the Sellmeier coefficients. These coefficients can be found in glass catalogs provided from manufacturers and are usually valid from the near-ultraviolet to the near-infrared. For wavelengths beyond this range, it is necessary to know the material's transmittance with respect to wavelength. From the dispersion formula, the temperature dependence of refractive index can be written:

d n a b s ( λ ,   T ) d T = n ( λ ,   T 0 ) 2 − 1 2 n ( λ ,   T 0 ) ( D 0 + 2 D 1 Δ T + 3 D 2 Δ T 2 + E 0 + 2 E 1 Δ T λ 2 − λ T K 2 ) {\displaystyle {\frac {dn_{abs\left(\lambda ,\ T\right)}}{dT}}={\frac {n_{\left(\lambda ,\ T_{0}\right)}^{2}-1}{2n_{\left(\lambda ,\ T_{0}\right)}}}\left(D_{0}+2D_{1}\Delta T+3D_{2}\Delta T^{2}+{\frac {E_{0}+2E_{1}\Delta T}{\lambda ^{2}-\lambda _{TK}^{2}}}\right)\,}

and

n ( λ ,   T ) = ( 1 + Δ T d n a b s ( λ ,   T ) d T ) n ( λ ,   T 0 ) {\displaystyle n_{\left(\lambda ,\ T\right)}=\left(1+\Delta T{\frac {dn_{abs\left(\lambda ,\ T\right)}}{dT}}\right)n_{\left(\lambda ,\ T_{0}\right)}\,}

Where D 0 {\textstyle D_{0}} , D 1 {\textstyle D_{1}} , D 2 {\textstyle D_{2}} , E 0 {\textstyle E_{0}} , E 1 {\textstyle E_{1}} , and λ T K {\textstyle \lambda _{TK}} are glass-dependent constants for an optic in vacuum. The power of an optic as a function of temperature can be written from the equations for extensive and intensive property changes, in addition to the lensmaker's equation.

Φ l e n s ( λ ,   T ) = ( n ( λ ,   T ) − 1 ) ( 1 R 1 ( T ) − 1 R 2 ( T ) + ( n ( λ ,   T ) − 1 ) L ( T ) n ( T ) R 1 ( T ) R 2 ( T ) ) {\displaystyle \Phi _{lens\left(\lambda ,\ T\right)}=\left(n_{\left(\lambda ,\ T\right)}-1\right)\left({\frac {1}{R_{1\left(T\right)}}}-{\frac {1}{R_{2\left(T\right)}}}+{\frac {\left(n_{\left(\lambda ,\ T\right)}-1\right)L_{\left(T\right)}}{{n_{\left(T\right)}R}_{1\left(T\right)}R_{2\left(T\right)}}}\right)\,}
Φ m i r r o r   ( T ) = − 2 R ( T ) {\displaystyle \Phi _{mirror\ \left(T\right)}={\frac {-2}{R_{(T)}}}\,}

Where Φ {\textstyle \Phi } is optical power, R {\textstyle R} is the radius of curvature, L {\textstyle L} is the thickness of the lens. These equations assume spherical surfaces of curvature. If a system is not in vacuum, the index of refraction for air will vary with temperature and pressure according to the Ciddor equation, a modified version of the Edlén equation.

Comparison of optical performance over temperature with different mechanical housing materials for a positive N-BK7 singlet designed at 22 C. "No thermal expansion" still includes effects from dn/dT.

Athermalization techniques

To account for optical variations introduced by extensive and intensive property changes in materials, systems can be athermalized through material selection or feedback loops.

Passive athermalization

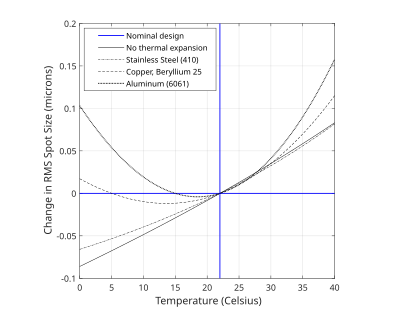
Passive athermalization works by choosing materials for a system that will compensate the overall change in system performance. The simplest way to do this is to choose materials for the optics and mechanics which have low CTE and d n d T {\textstyle {\frac {dn}{dT}}} values. This technique is not always possible as glass types are primarily chosen based on their refractive index and dispersion characteristics at operating temperature. Alternatively, mechanical materials can be chosen which have CTE values complementary to the change in focus introduced by the optics. A material with the preferred CTE is not always available, so two materials can be used in conjunction to effectively get the desired CTE value. Negative thermal expansion materials have recently increased the range of potential CTEs available, expanding passive athermalization options.

Active athermalization

When optical designs do not permit the selection of materials based on their thermal characteristics, passive athermalization may not be a viable technique. For example, the use of germanium in mid to long wave infrared systems is common because of its exceptional optical properties (high index of refraction and low dispersion). Unfortunately, germanium is also known for its large d n d T {\textstyle {\frac {dn}{dT}}} value, which makes it difficult to passively athermalize.

Because the primary aberration induced by temperature change is defocus, an optical element, group, or focal plane can be mechanically moved to refocus a system and account for thermal changes. Actively athermalized systems are designed with a feedback loop including a motor, for the focusing mechanism, and temperature sensor, to indicate the magnitude of the focus adjustment.

Temperature gradients

When a system is not in thermal equilibrium, it complicates the process of determining system performance. A common temperature gradient to encounter is an axial gradient. This involves temperatures changing in a lens as a function of the thickness of the lens, or often along the optical axis. In optical lens design it is standard notation for the optical axis to be co-linear with the Z-axis in cartesian coordinates. A difference between the temperature of the first and second surface of a lens will cause the lens to bend. This affects each radius of curvature, therefor changing the optical power of the lens. The radius of curvature change is a function of the temperature gradient in the optic.

R = ( R 0 + Δ R ) = ( 1 − α R 0 d T d L ) R 0 {\displaystyle R=(R_{0}+\Delta R)=\left(1-\alpha R_{0}{\frac {dT}{dL}}\right)R_{0}\,}

Where L {\textstyle L} is the thickness of the lens. Radial gradients are less predictable as they may cause the shape of curvature to change, making spherical surfaces aspherical. Determining temperature gradients in an optomechanical system can quickly become an arduous task, requiring an intimate understanding of the heat sources and sinks in a system. Temperature gradients are determined by heat flow and can be a result of conduction, convection, or radiation. Whether steady-state or transient solutions are adequate for an analysis is determined by operating requirements, system design, and the environment. It can be beneficial to leverage the computational power of the finite element method to solve the applicable heat flow equations to determine the temperature gradients of optical and mechanical components.

External links

References

  1. ^ Bentley & Olson (2012). Field Guide to Lens Design. Bellingham, Washington USA: SPIE. p. 88. ISBN 978-0-8194-9164-0.
  2. Kenichi Iga; Yasuo Kokubun (1 November 2005). Encyclopedic Handbook of Integrated Optics. CRC Press. pp. 32–. ISBN 978-1-4200-2781-5.
  3. Jamieson (1981). "Thermal effects in optical systems" (PDF). Optical Engineering. 20 (2): 156. Bibcode:1981OptEn..20..156J. doi:10.1117/12.7972683. Retrieved 8 December 2020.
  4. ^ "Refractive Index and Dispersion" (PDF). us.schott.com. Schott AG. Retrieved 13 December 2020.
  5. ^ "Optical Glass Data Sheets" (PDF). www.schott.com. Schott AG. Retrieved 6 December 2020.
  6. ^ "Temperature Coefficient of the Refractive Index" (PDF). www.schott.com. Schott AG. Retrieved 7 December 2020.
  7. "Temperature Coefficient of Refractive Index (dn/dT)". www.pmoptics.com. Precision Micro-Optics. Retrieved 7 December 2020.
  8. Birch & Downs (1993). "An Updated Edlen Equation for the Refractive Index of Air". Metrologia. 30 (3): 155–162. Bibcode:1993Metro..30..155B. doi:10.1088/0026-1394/30/3/004. S2CID 250817121.
  9. Stone & Zimmerman. "Edlen or Ciddor? Guidance in Choosing the Equation". emtoolbox.nist.gov. National Institute of Standards and Technology. Retrieved 13 December 2020.
  10. ^ Schwertz & Burge (2012). Field Guide to Optomechanical Design and Analysis. Bellingham, Washington USA: SPIE. pp. 98–105. ISBN 978-0-8194-9161-9.
  11. Monroe, James A.; McAllister, Jeremy S.; Content, David; Zgarba, Jay (19 February 2020). "Negative thermal expansion ALLVAR Alloys for smaller optics". In Kress, Bernard C.; Peroz, Christophe (eds.). Optical Architectures for Displays and Sensing in Augmented, Virtual, and Mixed Reality (AR, VR, MR). Vol. 11310. pp. 296–303. Bibcode:2020SPIE11310E..13M. doi:10.1117/12.2546869. ISBN 9781510633872. S2CID 213607039.
  12. "Germanium". www.pmoptics.com. Precision Micro-Optics. Retrieved 14 December 2020.
  13. ^ Bayar & Farsakoğlu (2002). "Mechanically active athermalization of a forward looking infrared system". Infrared Physics & Technology. 43 (2): 91–99. Bibcode:2002InPhT..43...91B. doi:10.1016/S1350-4495(01)00124-4.
Categories: