Misplaced Pages

The scanning helium microscope (SHeM) is a form of microscopy that uses low-energy (5–100 meV) neutral helium atoms to image the surface of a sample without any damage to the sample caused by the imaging process. Since helium is inert and neutral, it can be used to study delicate and insulating surfaces. Images are formed by rastering a sample underneath an atom beam and monitoring the flux of atoms that are scattered into a detector at each point.

The technique is different from a scanning helium ion microscope, which uses charged helium ions that can cause damage to a surface.

Motivation

Microscopes can be divided into two general classes: those that illuminate the sample with a beam, and those that use a physical scanning probe. Scanning probe microscopies raster a small probe across the surface of a sample and monitor the interaction of the probe with the sample. The resolution of scanning probe microscopies is set by the size of the interaction region between the probe and the sample, which can be sufficiently small to allow atomic resolution. Using a physical tip (e.g. AFM or STM) does have some disadvantages though including a reasonably small imaging area and difficulty in observing structures with a large height variation over a small lateral distance.

Microscopes that use a beam have a fundamental limit on the minimum resolvable feature size, ${\displaystyle d_{\text{A}}}$, which is given by the Abbe diffraction limit,

${\displaystyle d_{\text{A}}={\frac {\lambda }{2n\sin {\theta }}},}$

where ${\displaystyle \lambda }$ is the wavelength of the probing wave, ${\displaystyle n}$ is the refractive index of the medium the wave is travelling in and the wave is converging to a spot with a half-angle of ${\displaystyle \theta }$. While it is possible to overcome the diffraction limit on resolution by using a near-field technique, it is usually quite difficult. Since the denominator of the above equation for the Abbe diffraction limit will be approximately two at best, the wavelength of the probe is the main factor in determining the minimum resolvable feature, which is typically about 1 μm for optical microscopy.

To overcome the diffraction limit, a probe that has a smaller wavelength is needed, which can be achieved using either light with a higher energy, or through using a matter wave.

X-rays have a much smaller wavelength than visible light, and therefore can achieve superior resolutions when compared to optical techniques. Projection X-ray imaging is conventionally used in medical applications, but high resolution imaging is achieved through scanning transmission X-ray microscopy (STXM). By focussing the X-rays to a small point and rastering across a sample, a very high resolution can be obtained with light. The small wavelength of X-rays comes at the expense of a high photon energy, meaning that X-rays can cause radiation damage. Additionally, X-rays are weakly interacting, so they will primarily interact with the bulk of the sample, making investigations of a surface difficult.

Matter waves have a much shorter wavelength than visible light and therefore can be used to study features below about 1 μm. The advent of electron microscopy opened up a variety of new materials that could be studied due to the enormous improvement in the resolution when compared to optical microscopy.

The de Broglie wavelength, ${\displaystyle \lambda }$, of a matter wave in terms of its kinetic energy, ${\displaystyle E}$, and particle mass, ${\displaystyle m}$, is given by

${\displaystyle \lambda ={\frac {h}{\sqrt {2mE}}}.}$

Hence, for an electron beam to resolve atomic structure, the wavelength of the matter wave would need be at least ${\displaystyle \lambda }$ = 1 Å, and therefore the beam energy would need to be given by ${\displaystyle E}$ > 100 eV.

Since electrons are charged, they can be manipulated using electromagnetic optics to form extremely small spot sizes on a surface. Due to the wavelength of an electron beam being low, the Abbe diffraction limit can be pushed below atomic resolution and electromagnetic lenses can be used to form very intense spots on the surface of a material. The optics in a scanning electron microscope usually require the beam energy to be in excess of 1 keV to produce the best-quality electron beam.

The high energy of the electrons leads to the electron beam interacting not only with the surface of a material, but forming a tear-drop interaction volume underneath the surface. While the spot size on the surface can be extremely low, the electrons will travel into the bulk and continue interacting with the sample. Transmission electron microscopy avoids the bulk interaction by only using thin samples, however usually the electron beam interacting with the bulk will limit the resolution of a scanning electron microscope.

The electron beam can also damage the material, destroying the structure that is to be studied due to the high beam energy. Electron beam damage can occur through a variety of different processes that are specimen-specific. Examples of beam damage include the breaking of bonds in a polymer, which changes the structure, and knock-on damage in metals that creates a vacancy in the lattice, which changes to the surface chemistry. Additionally, the electron beam is charged, which means that the surface of the sample needs to be conducting to avoid artefacts of charge accumulation in images. One method to mitigate the issue when imaging insulating surfaces is to use an environmental scanning electron microscope (ESEM).

Therefore, in general, electrons are often not particularly suited to studying delicate surfaces due to the high beam energy and lack of exclusive surface sensitivity. Instead, an alternative beam is required for the study of surfaces at low energy without disturbing the structure.

Given the equation for the de Broglie wavelength above, the same wavelength of a beam can be achieved at lower energies by using a beam of particles that have a higher mass. Thus, if the objective were to study the surface of a material at a resolution that is below that which can be achieved with optical microscopy, it may be appropriate to use atoms as a probe instead. While neutrons can be used as a probe, they are weakly interacting with matter and can only study the bulk structure of a material. Neutron imaging also requires a high flux of neutrons, which usually can only be provided by a nuclear reactor or particle accelerator.

A beam of helium atoms with a wavelength ${\displaystyle \lambda }$ = 1 Å has an energy of ${\displaystyle E\approx }$ 20 meV, which is about the same as the thermal energy. Using particles of a higher mass than that of an electron means that it is possible to obtain a beam with a wavelength suitable to probe length scales down to the atomic level with a much lower energy.

Thermal energy helium atom beams are exclusively surface sensitive, giving helium scattering an advantage over other techniques such as electron and x-ray scattering for surface studies. For the beam energies that are used, the helium atoms will have classical turning points 2–3 Å away from the surface atom cores. The turning point is well above the surface atom cores, meaning that the beam will only interact with the outermost electrons.

History

This section relies excessively on references to primary sources. Please improve this section by adding secondary or tertiary sources. Find sources: "Scanning helium microscopy" – news · newspapers · books · scholar · JSTOR (September 2023) (Learn how and when to remove this message)

The first discussion of obtaining an image of a surface using atoms was by King and Bigas, who showed that an image of a surface can be obtained by heating a sample and monitoring the atoms that evaporate from the surface. King and Bigas suggest that it could be possible to form an image by scattering atoms from the surface, though it was some time before this was demonstrated.

The idea of imaging with atoms instead of light was subsequently widely discussed in the literature. The initial approach to producing a helium microscope assumed that a focussing element is required to produce a high intensity beam of atoms. An early approach was to develop an atomic mirror, which is appealing since the focussing is independent of the velocity distribution of the incoming atoms. However the material challenges to produce an appropriate surface that is macroscopically curved and defect free on an atomic length-scale has proved too challenging so far. King and Bigas, showed that an image of a surface can be obtained by heating a sample and monitoring the atoms that evaporate from the surface. King and Bigas suggest it could be possible to form an image by scattering atoms from the surface, though it was some time before it was demonstrated.

Metastable atoms are atoms that have been excited out of the ground state, but remain in an excited state for a significant period of time. Microscopy using metastable atoms has been shown to be possible, where the metastable atoms release stored internal energy into the surface, releasing electrons that provide information on the electronic structure. The kinetic energy of the metastable atoms means that only the surface electronic structure is probed, but the large energy exchange when the metastable atom de-excites will still perturb delicate sample surfaces.

The first two-dimensional neutral helium images were obtained using a conventional Fresnel zone plate by Koch et al. in a transmission setup. Helium will not pass through a solid material, therefore a large change in the measured signal is obtained when a sample is placed between the source and the detector. By maximising the contrast and using transmission mode, it was much easier to verify the feasibility of the technique. However, the setup used by Koch et al. with a zone plate did not produce a high enough signal to observe the reflected signal from the surface at the time. Nevertheless, the focussing obtained with a zone plate offers the potential for improved resolution due to the small beam spot size in the future. Research into neutral helium microscopes that use a Fresnel zone plate is an active area in Holst’s group at the University of Bergen.

Since using a zone plate proved difficult due to the low focussing efficiency, alternative methods for forming a helium beam to produce images with atoms were explored.

Recent efforts have avoided focussing elements and instead are directly collimating a beam with a pinhole. The lack of atom optics means that the beam width will be significantly larger than in an electron microscope. The first published demonstration of a two-dimensional image formed by helium reflecting from the surface was by Witham and Sánchez, who used a pinhole to form the helium beam. A small pinhole is placed very close to a sample and the helium scattered into a large solid angle is fed to a detector. Images are collected by moving the sample around underneath the beam and monitoring how the scattered helium flux changes.

In parallel to the work by Witham and Sánchez, a proof of concept machine named the scanning helium microscope (SHeM) was being developed in Cambridge in collaboration with Dastoor's group from the University of Newcastle. The approach that was adopted was to simplify previous attempts that involved an atom mirror by using a pinhole, but to still use a conventional helium source to produce a high quality beam. Other differences from the Witham and Sánchez design include using a larger sample to pinhole distance, so that a larger variety of samples can be used and to use a smaller collection solid angle, so that it may be possible to observe more subtle contrast. These changes also reduced the total flux in the detector meaning that higher efficiency detectors are required (which in itself is an active area of research.

Image formation process

The atomic beam is formed through a supersonic expansion, which is a standard technique used in helium atom scattering. The centreline of the gas is selected by a skimmer to form an atom beam with a narrow velocity distribution. The gas is then further collimated by a pinhole to form a narrow beam, which is typically between 1–10 μm. The use of a focusing element (such as a zone plate) allows beam spot sizes below 1 μm to be achieved, but currently still comes with low signal intensity.

The gas then scatters from the surface and is collected into a detector. In order to measure the flux of the neutral helium atoms, they must first be ionised. The inertness of helium that makes it a gentle probe means that it is difficult to ionise and therefore reasonably aggressive electron bombardment is typically used to create the ions. A mass spectrometer setup is then used to select only the helium ions for detection.

Once the flux from a specific part of the surface is collected, the sample is moved underneath the beam to generate an image. By obtaining the value of the scattered flux across a grid of positions, then values can then be converted to an image.

The observed contrast in helium images has typically been dominated by the variation in topography of the sample. Typically, since the wavelength of the atom beam is small, surfaces appear extremely rough to the incoming atom beam. Therefore, the atoms are diffusely scattered and roughly follow Knudsen's Law (the atom equivalent of Lambert's cosine law in optics). However, more recently work has begun to see divergence from diffuse scattering due to effects such as diffraction and chemical contrast effects. However, the exact mechanisms for forming contrast in a helium microscope is an active field of research. Most cases have some complex combination of several contrast mechanisms making it difficult to disentangle the different contributions.

Combinations of images from multiple perspectives allows stereophotogrammetry to produce partial three dimensional images, especially valuable for biological samples subject to degradation in electron microscopes.

Optimal configurations

The optimal configurations of scanning helium microscopes are geometrical configurations that maximise the intensity of the imaging beam within a given lateral resolution and under certain technological constraints.

When designing a scanning helium microscope, scientists strive to maximise the intensity of the imaging beam while minimising its width. The reason behind this is that the beam's width gives the resolution of the microscope while its intensity is proportional to its signal to noise ratio. Due to their neutrality and high ionisation energy, neutral helium atoms are hard to detect. This makes high-intensity beams a crucial requirement for a viable scanning helium microscope.

In order to generate a high-intensity beam, scanning helium microscopes are designed to generate a supersonic expansion of the gas into vacuum, that accelerates neutral helium atoms to high velocities. Scanning helium microscopes exist in two different configurations: the pinhole configuration and the zone plate configuration. In the pinhole configuration, a small opening (the pinhole) selects a section of the supersonic expansion far away from its origin, which has previously been collimated by a skimmer (essentially, another small pinhole). This section then becomes the imaging beam. In the zone plate configuration a Fresnel zone plate focuses the atoms coming from a skimmer into a small focal spot.

Each of these configurations have different optimal designs, as they are defined by different optics equations.

Pinhole configuration

For the pinhole configuration the width of the beam (which we aim to minimise) is largely given by geometrical optics. The size of the beam at the sample plane is given by the lines connecting the skimmer edges with the pinhole edges. When the Fresnel number is very small (${\displaystyle F\ll 1}$), the beam width is also affected by Fraunhofer diffraction (see equation below).

${\displaystyle \Phi =2{\sqrt {2\ln 2/3}}{\sqrt {\delta ^{2}+3\sigma _{A}^{2}(1-\theta (F))}}.}$

In this equation ${\displaystyle \Phi }$ is the Full Width at Half Maximum of the beam, ${\displaystyle \delta }$ is the geometrical projection of the beam and ${\displaystyle \sigma _{A}}$ is the Airy diffraction term. ${\displaystyle \theta }$ is the Heaviside step function used here to indicate that the presence of the diffraction term depends on the value of the Fresnel number. Note that there are variations of this equation depending on what is defined as the "beam width" (for details compare and ). Due to the small wavelength of the helium beam, the Fraunhofer diffraction term can usually be omitted.

The intensity of the beam (which we aim to maximise) is given by the following equation (according to the Sikora and Andersen model):

${\displaystyle I=I_{0}{\frac {r_{ph}^{2}}{(R_{F}+a)^{2}}}\left(1-\exp \left\right).}$

Where ${\displaystyle I_{0}}$ is the total intensity stemming from the supersonic expansion nozzle (taken as a constant in the optimisation problem), ${\displaystyle r_{ph}}$ is the radius of the pinhole, S is the speed ratio of the beam, ${\displaystyle r_{S}}$ is the radius of the skimmer, ${\displaystyle R_{F}}$ is the radius of the supersonic expansion quitting surface (the point in the expansion from which atoms can be considered to travel in a straight line), ${\displaystyle x_{S}}$ is the distance between the nozzle and the skimmer and ${\displaystyle a}$ is the distance between the skimmer and the pinhole. There are several other versions of this equation that depend on the intensity model, but they all show a quadratic dependency on the pinhole radius (the bigger the pinhole, the more intensity) and an inverse quadratic dependency with the distance between the skimmer and the pinhole (the more the atoms spread, the less intensity).

By combining the two equations shown above, one can obtain that for a given beam width ${\displaystyle \Phi }$ for the geometrical optics regime the following values correspond to intensity maxima:

${\displaystyle r_{S}^{max}={\frac {\Phi a}{2W_{D}K}},\qquad r_{ph}^{max}={\frac {\Phi a}{2K(a+W_{D})}}.}$

In here, ${\displaystyle W_{D}}$ represents the working distance of the microscope and ${\displaystyle K=2{\sqrt {2\ln 2/3}}}$ is a constant that stems from the definition of the beam width. Note that both equations are given with respect to the distance between the skimmer and the pinhole, a. The global maximum of intensity can then be obtained numerically by replacing these values in the intensity equation above. In general, smaller skimmer radii coupled with smaller distances between the skimmer and the pinhole are preferred, leading in practice to the design of increasingly smaller pinhole microscopes.

Zone plate configuration

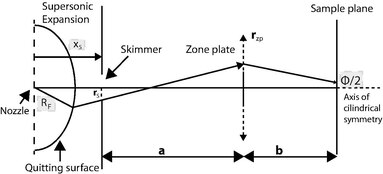
The zone plate microscope uses a zone plate (that acts roughly like as a classical lens) instead of a pinhole to focus the atom beam into a small focal spot. This means that the beam width equation changes significantly (see below).

${\displaystyle \Phi =K{\sqrt {\sigma _{cm}^{2}+\sigma _{A}^{2}+\left({\frac {Mr_{S}}{\sqrt {3}}}\right)^{2}}}\sim K{\sqrt {\left({\frac {r_{ZP}}{S{\sqrt {2}}}}\right)^{2}+0.42\Delta r+\left({\frac {Mr_{S}}{\sqrt {3}}}\right)^{2}}}.}$

Here, ${\displaystyle M}$ is the zone plate magnification and ${\displaystyle \Delta r}$ is the width of the smallest zone. Note the presence of chromatic aberrations (${\displaystyle \sigma _{cm}}$). The approximation sign indicates the regime in which the distance between the zone plate and the skimmer is much bigger than its focal length.

The first term in this equation is similar to the geometric contribution ${\displaystyle \delta }$ in the pinhole case: a bigger zone plate (taken all parameters constant) corresponds to a bigger focal spot size. The third term differs from the pinhole configuration optics as it includes a quadratic relation with the skimmer size (which is imaged through the zone plate) and a linear relation with the zone plate magnification, which will at the same time depend on its radius.

The equation to maximise, the intensity, is the same as the pinhole case with the substitution ${\displaystyle r_{ph}\leftrightarrow r_{ZP}}$. By substitution of the magnification equation:

${\displaystyle M={\frac {f}{a-f}}={\frac {2r_{ZP}\Delta r}{\lambda (a-2r_{ZP}\Delta r/\lambda )}},}$

where ${\displaystyle \lambda }$ is the average de-Broglie wavelength of the beam. Taking a constant ${\displaystyle \Delta r}$, which should be made equal to the smallest achievable value, the maxima of the intensity equation with respect to the zone plate radius and the skimmer-zone plate distance ${\displaystyle a}$ can be obtained analytically. The derivative of the intensity with respect to the zone plate radius can be reduced the following cubic equation (once it has been set equal to zero):

${\displaystyle a^{3}+2a^{2}\left(R_{F}-{\sqrt {3\Gamma }}r_{ZP}\right)+aR_{F}(R_{F}-4r_{ZP}{\sqrt {3\Gamma }})=r_{ZP}{\sqrt {3\Gamma }})R_{F}^{2}\left.}$

Here some groupings are used: ${\displaystyle \Gamma }$ is a constant that gives the relative size of the smallest aperture of the zone plate compared with the average wavelength of the beam and ${\displaystyle \Phi '}$ is the modified beam width, which is used through the derivation to avoid explicitly operating with the constant airy term: ${\displaystyle \Phi '^{2}=\sigma _{cm}^{2}+\left({\frac {Mr_{S}}{\sqrt {3}}}\right)^{2}}$.

This cubic equation is obtained under a series of geometrical assumptions and has a closed-form analytical solution that can be consulted in the original paper or obtained through any modern-day algebra software. The practical consequence of this equation is that zone plate microscopes are optimally designed when the distances between the components are small, and the radius of the zone plate is also small. This goes in line with the results obtained for the pinhole configuration, and has as its practical consequence the design of smaller scanning helium microscopes.

See also

• Helium atom scattering
• Atom optics
• Atomic mirror
• Matter wave

References

1. Williams, David B. (1996). Transmission electron microscopy: a textbook for materials science / David B. Williams and C. Barry Carter. New York, New York; London: Plenum. ISBN 978-0-306-45324-3.
2. Kardjilov, Nikolay; Manke, Ingo; Hilger, André; Strobl, Markus; Banhart, John (2011). "Neutron imaging in materials science". Materials Today. 14 (6): 248–256. doi:10.1016/S1369-7021(11)70139-0. ISSN 1369-7021.
3. Farias, Daniel; Rieder, Karl-Heinz (1998-12-01). "Atomic beam diffraction from solid surfaces". Reports on Progress in Physics. 61 (12): 1575. Bibcode:1998RPPh...61.1575F. doi:10.1088/0034-4885/61/12/001. ISSN 0034-4885. S2CID 250862443.
4. ^ King, John G.; Bigas, William R. (1969-04-19). "Molecular Scanner". Nature. 222 (5190): 261–263. Bibcode:1969Natur.222..261K. doi:10.1038/222261a0. S2CID 4152539.
5. Poelsema, Bene (1989). Scattering of Thermal Energy Atoms from Disordered Surfaces. Berlin: Springer-Verlag. ISBN 978-0-387-50358-5.
6. Hulpke, Erika (1992). Helium Atom Scattering from Surfaces. Berlin: Springer-Verlag. ISBN 978-3-540-54605-4.
7. Berkhout, J.; Luiten, O.; Setija, I.; Hijmans, T.; Mizusaki, T.; Walraven, J. (1989). "Quantum reflection: Focusing of hydrogen atoms with a concave mirror" (PDF). Physical Review Letters. 63 (16): 1689–1692. Bibcode:1989PhRvL..63.1689B. doi:10.1103/PhysRevLett.63.1689. PMID 10040645.
8. ^ Holst, B.; Allison, W. (1997). "An atom-focusing mirror". Nature. 390 (6657): 244. Bibcode:1997Natur.390..244H. doi:10.1038/36769. S2CID 4428642.
9. ^ Doak, R.; Grisenti, R.; Rehbein, S.; Schmahl, G.; Toennies, J.; W ll, C. (1999). "Towards Realization of an Atomic de Broglie Microscope: Helium Atom Focusing Using Fresnel Zone Plates". Physical Review Letters. 83 (21): 4229. Bibcode:1999PhRvL..83.4229D. doi:10.1103/PhysRevLett.83.4229.
10. Barredo, D.; Calleja, F.; Weeks, A. E.; Nieto, P.; Hinarejos, J. J.; Laurent, G.; Vazquez de Parga, A. L.; MacLaren, D. A.; Farías, D.; Allison, W.; Miranda, R. (2007-01-01). "Si(111)–H(1×1): A mirror for atoms characterized by AFM, STM, He and H2 diffraction". Surface Science. 601 (1): 24–29. Bibcode:2007SurSc.601...24B. doi:10.1016/j.susc.2006.08.048. ISSN 0039-6028.
11. Fladischer, K.; Reingruber, H.; Reisinger, T.; Mayrhofer, V.; Ernst, W. E.; Ross, A. E.; MacLaren, D. A.; Allison, W.; D Litwin; Galas, J.; Sitarek, S.; Nieto, P.; Barredo, D.; Farías, D.; Miranda, R.; Surma, B.; Miros, A.; Piatkowski, B.; E Søndergård; Holst, B. (2010). "An ellipsoidal mirror for focusing neutral atomic and molecular beams" (PDF). New Journal of Physics. 12 (3): 033018. Bibcode:2010NJPh...12c3018F. doi:10.1088/1367-2630/12/3/033018. ISSN 1367-2630. S2CID 58941708.
12. Harada, Y.; Yamamoto, S.; Aoki, M.; Masuda, S.; Ichinokawa, T.; Kato, M.; Sakai, Y. (1994). "Surface spectroscopy with high spatial resolution using metastable atoms". Nature. 372 (6507): 657–659. Bibcode:1994Natur.372..657H. doi:10.1038/372657a0. ISSN 1476-4687. S2CID 4301218.
13. Yamamoto, Susumu; Masuda, Shigeru; Yasufuku, Hideyuki; Ueno, Nobuo; Harada, Yoshiya; Ichinokawa, Takeo; Kato, Makoto; Sakai, Yuji (1997-09-15). "Study of solid surfaces by metastable electron emission microscopy: Energy-filtered images and local electron spectra at the outermost surface layer of silicon oxide on Si(100)". Journal of Applied Physics. 82 (6): 2954–2960. Bibcode:1997JAP....82.2954Y. doi:10.1063/1.366130. ISSN 0021-8979.
14. Koch, M.; Rehbein, S.; Schmahl, G.; Reisinger, T.; Bracco, G.; Ernst, W. E.; Holst, B. (2008-01-01). "Imaging with neutral atoms—a new matter-wave microscope". Journal of Microscopy. 229 (1): 1–5. doi:10.1111/j.1365-2818.2007.01874.x. ISSN 1365-2818. PMID 18173637. S2CID 1792264.
15. Witham, Philip; Sánchez, Erik (2011-10-01). "A simple approach to neutral atom microscopy". Review of Scientific Instruments. 82 (10): 103705–103705–9. Bibcode:2011RScI...82j3705W. doi:10.1063/1.3650719. eISSN 1089-7623. ISSN 0034-6748. PMID 22047301. S2CID 35615416.
16. Barr, M.; Fahy, A.; Jardine, A.; Ellis, J.; Ward, D.; MacLaren, D. A.; Allison, W.; Dastoor, P. C. (2014-12-01). "A design for a pinhole scanning helium microscope" (PDF). Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 20th International Workshop on Inelastic Ion-Surface Collisions (IISC-20). 340: 76–80. Bibcode:2014NIMPB.340...76B. doi:10.1016/j.nimb.2014.06.028. ISSN 0168-583X.
17. Alderwick, A. R.; Jardine, A. P.; Hedgeland, H.; MacLaren, D. A.; Allison, W.; Ellis, J. (December 2008). "Simulation and analysis of solenoidal ion sources" (PDF). The Review of Scientific Instruments. 79 (12): 123301–123301–9. Bibcode:2008RScI...79l3301A. doi:10.1063/1.3030858. ISSN 1089-7623. PMID 19123556.
18. ^ Bergin, Matthew (2019-04-27). Instrumentation and contrast mechanisms in scanning helium microscopy (Thesis). University of Cambridge. doi:10.17863/CAM.37853. Retrieved 2019-03-19.
19. Barr, M.; Fahy, A.; Martens, J.; Jardine, A. P.; Ward, D. J.; Ellis, J.; Allison, W.; Dastoor, P. C. (April 2016). "Unlocking new contrast in a scanning helium microscope". Nature Communications. 7 (1): 10189. Bibcode:2016NatCo...710189B. doi:10.1038/ncomms10189. ISSN 2041-1723. PMC 4725762. PMID 26727303.
20. Myles, Thomas A.; Eder, Sabrina D.; Barr, Matthew G.; Fahy, Adam; Martens, Joel; Dastoor, Paul C. (2019-02-14). "Taxonomy through the lens of neutral helium microscopy". Scientific Reports. 9 (1). Springer Science and Business Media LLC: 2148. Bibcode:2019NatSR...9.2148M. doi:10.1038/s41598-018-36373-5. ISSN 2045-2322. PMC 6375913. PMID 30765723.
21. ^ Bergin, M.; Ward, D. J.; Ellis, J.; Jardine, A. P. (December 2019). "A method for constrained optimisation of the design of a scanning helium microscope". Ultramicroscopy. 207: 112833. doi:10.1016/j.ultramic.2019.112833. ISSN 1879-2723. PMID 31494478. S2CID 202003302.
22. ^ Palau, Adrià Salvador; Bracco, Gianangelo; Holst, Bodil (2016-12-20). "Theoretical model of the helium pinhole microscope". Physical Review A. 94 (6): 063624. Bibcode:2016PhRvA..94f3624P. doi:10.1103/PhysRevA.94.063624. hdl:11567/865704.
23. Bracco, Gianangelo; Holst, Bodil, eds. (2013). Surface Science Techniques. Springer Series in Surface Sciences. Vol. 51. Bibcode:2013sst..book.....B. doi:10.1007/978-3-642-34243-1. ISBN 978-3-642-34242-4. ISSN 0931-5195. S2CID 137147527.
24. Barr, M.; Fahy, A.; Jardine, A.; Ellis, J.; Ward, D.; MacLaren, D. A.; Allison, W.; Dastoor, P. C. (2014-12-01). "A design for a pinhole scanning helium microscope". Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 20th International Workshop on Inelastic Ion-Surface Collisions (IISC-20). 340: 76–80. Bibcode:2014NIMPB.340...76B. doi:10.1016/j.nimb.2014.06.028. ISSN 0168-583X.
25. Eder, S D; Reisinger, T; Greve, M M; Bracco, G; Holst, B (2012-07-06). "Focusing of a neutral helium beam below one micron". New Journal of Physics. 14 (7): 073014. Bibcode:2012NJPh...14g3014E. doi:10.1088/1367-2630/14/7/073014. ISSN 1367-2630. S2CID 120314620.
26. Sikora, Gary S. (1973). Analysis of Asymptotic Behavior of Free Jets: Prediction of Molecular Beam Intensity and Velocity Distributions. Princeton University.
27. ^ Salvador Palau, Adrià; Bracco, Gianangelo; Holst, Bodil (2017-01-12). "Theoretical model of the helium zone plate microscope". Physical Review A. 95 (1): 013611. Bibcode:2017PhRvA..95a3611S. doi:10.1103/PhysRevA.95.013611. hdl:11567/865709.

• Microscopes
• Nanotechnology
• Atomic, molecular, and optical physics