| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Band-stop filter" – news · newspapers · books · scholar · JSTOR (June 2010) (Learn how and when to remove this message) |

In signal processing, a band-stop filter or band-rejection filter is a filter that passes most frequencies unaltered, but attenuates those in a specific range to very low levels. It is the inverse of a band-pass filter. A notch filter is a band-stop filter with a narrow stopband (high Q factor).
Narrow notch filters (optical) are used in Raman spectroscopy, live sound reproduction (public address systems, or PA systems) and in instrument amplifiers (especially amplifiers or preamplifiers for acoustic instruments such as acoustic guitar, mandolin, bass instrument amplifier, etc.) to reduce or prevent audio feedback, while having little noticeable effect on the rest of the frequency spectrum (electronic or software filters). Other names include "band limit filter", "T-notch filter", "band-elimination filter", and "band-reject filter".
Typically, the width of the stopband is 1 to 2 decades (that is, the highest frequency attenuated is 10 to 100 times the lowest frequency attenuated). However, in the audio band, a notch filter has high and low frequencies that may be only semitones apart. From the figure of the frequency response of an ideal band-stop filter, it's obvious that the band-stop filter is simply an inverted band-pass filter where they share same definition of bandwidth, pass band, stop band and center frequency. The attenuation should be infinite in the stop band and be zero in the two pass bands for an ideal band-stop filter. Band-stop filters are designed by the combination of a low-pass filter and a high-pass filter in a parallel configuration. Overlapping does not occur in the summation of high-pass filter and low-pass filter during the design of band-stop filter. The difference in the starting and ending frequency points causes the two filters to connect effectively without any overlapping.
Mathematical description
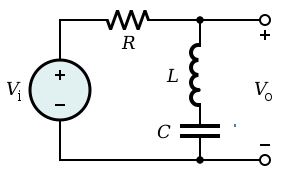
Band-stop filter can be represented as a combination of low-pass and high-pass filters if the bandwidth is wide enough that the two filters do not interact too much. A more general approach is to design as a low-pass prototype filter which can then be transformed into a bandstop. The simple notch filter shown can be directly analysed. The transfer function is,
Here is zero circular frequency and is the pole circular frequency. Zero frequency is the cutoff frequency and sets the type of the notch filter: standard notch when , low-pass notch () and high-pass notch () filters. denotes the Q-factor.
For standard notch filter the formulation can be rewritten as
where is the central rejected frequency and is the width of the rejected band.
Examples
In the audio domain
- Anti-hum filter
For countries using 60 Hz power lines:
- low frequency: 59 Hz,
- middle frequency: 60 Hz,
- high frequency: 61 Hz.
This means that the filter passes all frequencies, except for the range of 59–61 Hz. This would be used to filter out the mains hum from the 60 Hz power line, though its higher harmonics could still be present.
For countries where power transmission is at 50 Hz, the filter would have a 49–51 Hz range.
In the radio-frequency (RF) domain
- Non-linearities of power amplifiers
When measuring the non-linearities of power amplifiers, a very narrow notch filter can be very useful to avoid the carrier frequency. Use of the filter may ensure that the maximum input power of a spectrum analyser used to detect spurious content will not be exceeded.
- Wave trap
A notch filter, usually a simple LC circuit, is used to remove a specific interfering frequency. This is a technique used with radio receivers that are so close to a transmitter that it swamps all other signals. The wave trap is used to remove or greatly reduce the signal from the nearby transmitter.
- Software-defined radio
Most affordable software-defined radios (SDR) on the market today suffer from limited dynamic and operating ranges. In other words, in real-world operating environments, a SDR can easily be saturated by a strong signal. In particular FM broadcast signals are very strong and nearly everywhere. These signals can prevent a SDR from processing other weak signals. FM notch filters are very useful for SDR applications and have increased in their popularity.
Optical filtering (wavelength selection)
In optics, there are several methods of filtering selected wavelengths from a source or to a detector. They rely on scattering or destructive interference.
Filtering by scattering and diffraction
A diffraction grating or a dispersive prism may be used to selectively redirect selected wavelengths of light within an optical system.
In the case of transmission gratings and prisms, polychromatic light that passes through the object will be redirected according to wavelength. A slit may then be used to select wavelengths that are desired. A reflective grating may also be utilized for the same purpose, though in this case light is reflected rather than transmitted. Filters of this design may be high-pass, band-pass, or low-pass, depending on system configuration.
Filtering by interference
When using optics with real materials, light will be attenuated at various wavelengths through interference with the medium through which the light traversed. In this sense, material selection may be utilized to selectively filter light according to the wavelengths that are minimally attenuated. To some extent, all real optical systems will suffer from this phenomenon.
Alternatively, it is also possible to use an oscillating reflecting surface to cause destructive interference with reflected light along a single optical path. This principle is the basis for a Michelson interferometer.
Band-stop smoothing filter
Smoothing filter is essential in many fields, such as signal and image processing, computer vision, statistics, stated by Roonizi (2021). Algorithms such as quadratic variation regularization and smoothness priors are the most common way to perform signal denoising. These algorithms are implemented to band-stop smoothing filters and being investigated by Roonizi (2021). A naive band-stop smoothing filter is raised, which is constructed by connecting a high-pass smoothing filter and a low-pass smoothing filter. These two smoothing filter sections are configured in parallel way. Moreover, it was suggested that positive noise correlation promises to obtain the best band-stop smoothing filter.
Telecommunications
The development of telecommunications applications raises the demand of radio frequency and microwave filters, stated by Haddi (2019). Those filters are commonly used in PA systems (Public Address Systems) and speaker systems to produce audio with great quality. Microwave filters have high flexibility of actualization and low cost. The band-stop filter in the telecommunications field, has a respectable place which it is essential for microwave transceivers. For example, wireless communication systems make use of band-stop filters to achieve the requirement of miniaturization.
Microstrip Band-stop Filter
Microstrip-line band-stop filter is convenient to implement with low cost and light weight. Hsieh & Wang (2005) stated that, conventional microstrip band-stop filters are made of shunt open-circuited resonators. They usually has the characteristic of having narrow stopband. However, alternating the band-stop filter to have a wide stop band response with specific design can bring huge advantage over the conventional band-stop filters.
The advantages of the microstrip band-stop filter designed by Hsieh & Wang (2005) is its compact size and easy implementation. This improved band-stop filter with wide stop-band has additional amount of transmission zeros. The purpose of this design is to combine a shunt open-circuited quarter-wavelength resonator with one section of quarter-wavelength frequency-selecting coupling structure, stated by Hsieh & Wang (2005). As a result, a simple structured band-stop filter with easy implementation can bring advantages of lower-order resonators, great stop band performance when compared to conventional microstrip band-stop filters.
See also
References
- "Band-stop filter", Federal Standard 1037C, accessed 14 May 2018.
- "Chapter 8: Analog Filters". Basic Linear Design. USA: Analog Devices Inc. 2006.
- Carr, Joseph J. (2001). The technician's radio receiver handbook: Wireless and telecommunication technology, p. 282. Newnes. ISBN 0-7506-7319-2.
- Terracciano, Anthony (2018). "Hazardous Gas Detection Sensor Using Broadband Light-Emitting Diode-Based Absorption Spectroscopy for Space Applications". New Space. 6 (1): 28–36. Bibcode:2018NewSp...6...28T. doi:10.1089/space.2017.0044. OSTI 1435270.
- ^ Roonizi, Arman Kheirati; Jutten, Christian (2021). "Band-Stop Smoothing Filter Design". IEEE Transactions on Signal Processing. 69: 1797–1810. Bibcode:2021ITSP...69.1797R. doi:10.1109/TSP.2021.3060619. ISSN 1941-0476. S2CID 233137801.
- Haddi, Souhaila Ben; Zugari, Asmaa; Zakriti, Alia; Achraou, Soufiane (2020-01-01). "Design of a Band-Stop Planar Filter for Telecommunications Applications". Procedia Manufacturing. 46: 788–792. doi:10.1016/j.promfg.2020.04.006. ISSN 2351-9789. S2CID 219444573.
- Hsieh, Ming-Yu; Wang, Shih-Ming (July 2005). "Compact and wideband microstrip bandstop filter". IEEE Microwave and Wireless Components Letters. 15 (7): 472–474. doi:10.1109/LMWC.2005.851572. ISSN 1558-1764.
| Signal-processing filters | |
|---|---|
| Electronic filter |

 is zero circular frequency and
is zero circular frequency and  is the pole circular frequency. Zero frequency is the cutoff frequency and
is the pole circular frequency. Zero frequency is the cutoff frequency and  , low-pass notch (
, low-pass notch ( ) and high-pass notch (
) and high-pass notch ( ) filters.
) filters.  denotes the Q-factor.
denotes the Q-factor.

 is the central rejected frequency and
is the central rejected frequency and  is the width of the rejected band.
is the width of the rejected band.