Misplaced Pages

A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Misplaced Pages's content policies, particularly neutral point of view. Please discuss further on the talk page. (December 2017) (Learn how and when to remove this message)

Computational anatomy (CA) is a discipline within medical imaging focusing on the study of anatomical shape and form at the visible or gross anatomical scale of morphology. The field is broadly defined and includes foundations in anatomy, applied mathematics and pure mathematics, including medical imaging, neuroscience, physics, probability, and statistics. It focuses on the anatomical structures being imaged, rather than the medical imaging devices. The central focus of the sub-field of computational anatomy within medical imaging is mapping information across anatomical coordinate systems most often dense information measured within a magnetic resonance image (MRI). The introduction of flows into CA, which are akin to the equations of motion used in fluid dynamics, exploit the notion that dense coordinates in image analysis follow the Lagrangian and Eulerian equations of motion. In models based on Lagrangian and Eulerian flows of diffeomorphisms, the constraint is associated to topological properties, such as open sets being preserved, coordinates not crossing implying uniqueness and existence of the inverse mapping, and connected sets remaining connected. The use of diffeomorphic methods grew quickly to dominate the field of mapping methods post Christensen's original paper, with fast and symmetric methods becoming available.

The main statistical model

The central statistical model of Computational Anatomy in the context of medical imaging has been the source-channel model of Shannon theory; the source is the deformable template of images ${\displaystyle I\in {\mathcal {I}}}$, the channel outputs are the imaging sensors with observables ${\displaystyle I^{D}\in {\mathcal {I}}^{\mathcal {D}}}$ (see Figure). The importance of the source-channel model is that the variation in the anatomical configuration are modelled separated from the sensor variations of the Medical imagery. The Bayes theory dictates that the model is characterized by the prior on the source, ${\displaystyle \pi _{\mathcal {I}}(\cdot )}$ on ${\displaystyle I\in {\mathcal {I}}}$, and the conditional density on the observable

${\displaystyle p(\cdot \mid I){\text{ on }}I^{D}\in {\mathcal {I}}^{\mathcal {D}}}$

conditioned on ${\displaystyle I\in {\mathcal {I}}}$.

In deformable template theory, the images are linked to the templates, with the deformations a group which acts on the template; see group action in computational anatomy For image action ${\displaystyle I(g)\doteq g\cdot I_{\mathrm {temp} },g\in {\mathcal {G}}}$, then the prior on the group ${\displaystyle \pi _{\mathcal {G}}(\cdot )}$ induces the prior on images ${\displaystyle \pi _{\mathcal {I}}(\cdot )}$, written as densities the log-posterior takes the form

${\displaystyle \log p(I(g)\mid I^{D})\simeq \log p(I^{D}\mid I(g))+\log \pi _{\mathcal {G}}(g).}$

The random orbit model which follows specifies how to generate the group elements and therefore the random spray of objects which form the prior distribution.

The random orbit model of computational anatomy

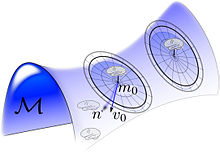
The random orbit model of Computational Anatomy first appeared in modelling the change in coordinates associated to the randomness of the group acting on the templates, which induces the randomness on the source of images in the anatomical orbit of shapes and forms and resulting observations through the medical imaging devices. Such a random orbit model in which randomness on the group induces randomness on the images was examined for the Special Euclidean Group for object recognition in which the group element ${\displaystyle g\in {\mathcal {G}}}$ was the special Euclidean group in.

For the study of deformable shape in CA, the high-dimensional diffeomorphism groups used in computational anatomy are generated via smooth flows ${\displaystyle \varphi _{t},t\in }$ which satisfy the Lagrangian and Eulerian specification of the flow fields satisfying the ordinary differential equation:

${\displaystyle {\frac {d}{dt}}\varphi _{t}=v_{t}\circ \varphi _{t},\ \varphi _{0}=\operatorname {id} \ ;}$

(Lagrangian flow)

with ${\displaystyle v\doteq (v_{1},v_{2},v_{3})}$ the vector fields on ${\displaystyle {\mathbb {R} }^{3}}$ termed the Eulerian velocity of the particles at position ${\displaystyle \varphi }$ of the flow. The vector fields are functions in a function space, modelled as a smooth Hilbert space with the vector fields having 1-continuous derivative . For ${\displaystyle v_{t}={\dot {\varphi }}_{t}\circ \varphi _{t}^{-1},t\in }$, the inverse of the flow is given by

${\displaystyle {\frac {d}{dt}}\varphi _{t}^{-1}=-(D\varphi _{t}^{-1})v_{t},\ \varphi _{0}^{-1}=\operatorname {id} ,}$

(Eulerianflow)

and the ${\displaystyle 3\times 3}$ Jacobian matrix for flows in ${\displaystyle \mathbb {R} ^{3}}$ given as ${\displaystyle \ D\varphi \doteq \left({\frac {\partial \varphi _{i}}{\partial x_{j}}}\right).}$

To ensure smooth flows of diffeomorphisms with inverse, the vector fields ${\displaystyle {\mathbb {R} }^{3}}$ must be at least 1-time continuously differentiable in space which are modelled as elements of the Hilbert space ${\displaystyle (V,\|\cdot \|_{V})}$ using the Sobolev embedding theorems so that each element ${\displaystyle v_{i}\in H_{0}^{3},i=1,2,3,}$ has 3-square-integrable derivatives. Thus ${\displaystyle (V,\|\cdot \|_{V})}$ embed smoothly in 1-time continuously differentiable functions. The diffeomorphism group are flows with vector fields absolutely integrable in Sobolev norm:

${\displaystyle \operatorname {Diff} _{V}\doteq \left\{\varphi =\varphi _{1}:{\dot {\varphi }}_{t}=v_{t}\circ \varphi _{t},\varphi _{0}=\operatorname {id} ,\int _{0}^{1}\|v_{t}\|_{V}\,dt<\infty \right\},}$

(Diffeomorphism group)

where ${\displaystyle \|v_{t}\|_{V}^{2}\doteq \int _{X}Av_{t}\cdot v_{t}dx}$ with ${\displaystyle A}$ a linear operator ${\displaystyle A:V\mapsto V^{*}}$ defining the norm of the RKHS. The integral is calculated by integration by parts when ${\displaystyle Av}$ is a generalized function in the dual space ${\displaystyle V^{*}}$.

Riemannian exponential

In the random orbit model of computational anatomy, the entire flow is reduced to the initial condition which forms the coordinates encoding the diffeomorphism. From the initial condition ${\displaystyle v_{0}}$ then geodesic positioning with respect to the Riemannian metric of Computational anatomy solves for the flow of the Euler-Lagrange equation. Solving the geodesic from the initial condition ${\displaystyle v_{0}}$ is termed the Riemannian-exponential, a mapping ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(\cdot ):V\to \operatorname {Diff} _{V}}$ at identity to the group.

The Riemannian exponential satisfies ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{0})=\varphi _{1}}$ for initial condition ${\displaystyle {\dot {\varphi }}_{0}=v_{0}}$, vector field dynamics ${\displaystyle {\dot {\varphi }}_{t}=v_{t}\circ \varphi _{t},t\in }$,

• for classical equation diffeomorphic shape momentum ${\displaystyle \int _{X}Av_{t}\cdot w\,dx}$, ${\displaystyle Av\in V}$, then

${\displaystyle {\frac {d}{dt}}Av_{t}+(Dv_{t})^{T}Av_{t}+(DAv_{t})v_{t}+(\nabla \cdot v)Av_{t}=0\ ;}$

• for generalized equation, then ${\displaystyle Av\in V^{*}}$, ${\displaystyle w\in V}$

${\displaystyle \int _{X}{\frac {d}{dt}}Av_{t}\cdot w\,dx+\int _{X}Av_{t}\cdot ((Dv_{t})w-(Dw)v_{t})\,dx=0.}$

It is extended to the entire group, ${\displaystyle \varphi =\operatorname {Exp} _{\varphi }(v_{0}\circ \varphi )\doteq \operatorname {Exp} _{\mathrm {id} }(v_{0})\circ \varphi .}$ Depicted in the accompanying figure is a depiction of the random orbits around each exemplar, ${\displaystyle m_{0}\in {\mathcal {M}}}$, generated by randomizing the flow by generating the initial tangent space vector field at the identity ${\displaystyle v_{0}\in V}$, and then generating random object ${\displaystyle n\doteq \operatorname {Exp} _{\mathrm {id} }(v_{0})\cdot m_{0}\in {\mathcal {M}}}$.

Shown in the Figure on the right the cartoon orbit, are a random spray of the subcortical manifolds generated by randomizing the vector fields ${\displaystyle v_{0}}$ supported over the submanifolds. The random orbit model induces the prior on shapes and images ${\displaystyle I\in {\mathcal {I}}}$ conditioned on a particular atlas ${\displaystyle I_{a}\in {\mathcal {I}}}$. For this the generative model generates the mean field ${\displaystyle I}$ as a random change in coordinates of the template according to ${\displaystyle I\doteq \varphi \cdot I_{a}}$, where the diffeomorphic change in coordinates is generated randomly via the geodesic flows.

MAP estimation in the multiple-atlas orbit model

The random orbit model induces the prior on shapes and images ${\displaystyle I\in {\mathcal {I}}}$ conditioned on a particular atlas ${\displaystyle I_{a}\in {\mathcal {I}}}$. For this the generative model generates the mean field ${\displaystyle I}$ as a random change in coordinates of the template according to ${\displaystyle I\doteq \varphi \cdot I_{a}}$, where the diffeomorphic change in coordinates is generated randomly via the geodesic flows. The prior on random transformations ${\displaystyle \pi _{\mathrm {Diff} }(d\varphi )}$ on ${\displaystyle \operatorname {Diff} _{V}}$ is induced by the flow ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v)}$, with ${\displaystyle v\in V}$ constructed as a Gaussian random field prior ${\displaystyle \pi _{V}(dv)}$. The density on the random observables at the output of the sensor ${\displaystyle I^{D}\in {\mathcal {I}}^{D}}$ are given by

${\displaystyle p(I^{D}\mid I_{a})=\int _{V}p(I^{D}\mid \operatorname {Exp} _{\mathrm {id} }(v)\cdot I_{a})\pi _{V}(dv)\ .}$

Maximum a posteriori estimation (MAP) estimation is central to modern statistical theory. Parameters of interest ${\displaystyle \theta \in \Theta }$ take many forms including (i) disease type such as neurodegenerative or neurodevelopmental diseases, (ii) structure type such as cortical or subcortical structures in problems associated to segmentation of images, and (iii) template reconstruction from populations. Given the observed image ${\displaystyle I^{D}}$, MAP estimation maximizes the posterior:

${\displaystyle {\hat {\theta }}\doteq \arg \max _{\theta \in \Theta }\log p(\theta \mid I^{D}).}$

This requires computation of the conditional probabilities ${\displaystyle p(\theta \mid I^{D})={\frac {p(I^{D},\theta )}{p(I^{D})}}}$. The multiple atlas orbit model randomizes over the denumerable set of atlases ${\displaystyle \{I_{a},a\in {\mathcal {A}}\}}$. The model on images in the orbit take the form of a multi-modal mixture distribution

${\displaystyle p(I^{D},\theta )=\sum _{a\in {\mathcal {A}}}p(I^{D},\theta \mid I_{a})\pi _{\mathcal {A}}(a)\ .}$

The conditional Gaussian model has been examined heavily for inexact matching in dense images and for landmark matching.

Dense emage matching

Model ${\displaystyle I^{D}(x),x\in X}$ as a conditionally Gaussian random field conditioned, mean field, ${\displaystyle \varphi _{1}\cdot I\doteq I(\varphi _{1}^{-1}),\varphi _{1}\in Diff_{V}}$. For uniform variance the endpoint error terms plays the role of the log-conditional (only a function of the mean field) giving the endpoint term:

Landmark matching

Model ${\displaystyle Y=\{y_{1},y_{2},\dots \}}$ as conditionally Gaussian with mean field ${\displaystyle \varphi _{1}(x_{i}),i=1,2,\dots ,\varphi _{1}\in \operatorname {Diff} _{V}}$, constant noise variance independent of landmarks. The log-conditional (only a function of the mean field) can be viewed as the endpoint term:

${\displaystyle -\log p(I^{D}\mid I(g))\simeq \operatorname {E} (\varphi _{1})\doteq {\frac {1}{2\sigma ^{2}}}\sum _{i}\|y_{i}-\varphi _{1}(x_{i})\|^{2}.}$

MAP segmentation based on multiple atlases

The random orbit model for multiple atlases models the orbit of shapes as the union over multiple anatomical orbits generated from the group action of diffeomorphisms, ${\displaystyle {\mathcal {I}}=\textstyle \bigcup _{a\in {\mathcal {A}}}\displaystyle \operatorname {Diff} _{V}\cdot I_{a}}$, with each atlas having a template and predefined segmentation field ${\displaystyle (I_{a},W_{a}),a=a_{1},a_{2},\ldots }$. incorporating the parcellation into anatomical structures of the coordinate of the MRI.. The pairs are indexed over the voxel lattice ${\displaystyle I_{a}(x_{i}),W_{a}(x_{i}),x_{i}\in X\subset {\mathbb {R} }^{3}}$ with an MRI image and a dense labelling of every voxel coordinate. The anatomical labelling of parcellated structures are manual delineations by neuroanatomists.

The Bayes segmentation problem is given measurement ${\displaystyle I^{D}}$ with mean field and parcellation ${\displaystyle (I,W)}$, the anatomical labelling ${\displaystyle \theta \doteq W}$. mustg be estimated for the measured MRI image. The mean-field of the observable ${\displaystyle I^{D}}$ image is modelled as a random deformation from one of the templates ${\displaystyle I\doteq \varphi \cdot I_{a}}$, which is also randomly selected, ${\displaystyle A=a}$,. The optimal diffeomorphism ${\displaystyle \varphi \in {\mathcal {G}}}$ is hidden and acts on the background space of coordinates of the randomly selected template image ${\displaystyle I_{a}}$. Given a single atlas ${\displaystyle a}$, the likelihood model for inference is determined by the joint probability ${\displaystyle p(I^{D},W\mid A=a)}$; with multiple atlases, the fusion of the likelihood functions yields the multi-modal mixture model with the prior averaging over models.

The MAP estimator of segmentation ${\displaystyle W_{a}}$ is the maximizer ${\displaystyle \max _{W}\log p(W\mid I^{D})}$ given ${\displaystyle I^{D}}$, which involves the mixture over all atlases.

${\displaystyle {\hat {W}}\doteq \arg \textstyle \max _{W}\displaystyle \log p(I^{D},W){\text{ with }}p(I^{D},W)=\textstyle \sum _{a\in {\mathcal {A}}}\displaystyle p(I^{D},W\mid A=a)\pi _{A}(a).}$

The quantity ${\displaystyle p(I^{D},W)}$ is computed via a fusion of likelihoods from multiple deformable atlases, with ${\displaystyle \pi _{A}(a)}$ being the prior probability that the observed image evolves from the specific template image ${\displaystyle I_{a}}$.

The MAP segmentation can be iteratively solved via the expectation–maximization algorithm

${\displaystyle W^{\text{new}}\doteq \arg \max _{W}\int \log p(W,I^{D},A,\varphi )\,dp(A,\varphi \mid W^{\text{old}},I^{D}).}$

MAP estimation of volume templates from populations and the EM algorithm

Generating templates empirically from populations is a fundamental operation ubiquitous to the discipline. Several methods based on Bayesian statistics have emerged for submanifolds and dense image volumes. For the dense image volume case, given the observable ${\displaystyle I^{D_{1}},I^{D_{2}},\dots }$ the problem is to estimate the template in the orbit of dense images ${\displaystyle I\in {\mathcal {I}}}$. Ma's procedure takes an initial hypertemplate ${\displaystyle I_{0}\in {\mathcal {I}}}$ as the starting point, and models the template in the orbit under the unknown to be estimated diffeomorphism ${\displaystyle I\doteq \varphi _{0}\cdot I_{0}}$, with the parameters to be estimated the log-coordinates ${\displaystyle \theta \doteq v_{0}}$ determining the geodesic mapping of the hyper-template ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{0})\cdot I_{0}=I\in {\mathcal {I}}}$.

In the Bayesian random orbit model of computational anatomy the observed MRI images ${\displaystyle I^{D_{i}}}$ are modelled as a conditionally Gaussian random field with mean field ${\displaystyle \varphi _{i}\cdot I}$, with ${\displaystyle \varphi _{i}}$ a random unknown transformation of the template. The MAP estimation problem is to estimate the unknown template ${\displaystyle I\in {\mathcal {I}}}$ given the observed MRI images.

Ma's procedure for dense imagery takes an initial hypertemplate ${\displaystyle I_{0}\in {\mathcal {I}}}$ as the starting point, and models the template in the orbit under the unknown to be estimated diffeomorphism ${\displaystyle I\doteq \varphi _{0}\cdot I_{0}}$. The observables are modelled as conditional random fields, ${\displaystyle I^{D_{i}}}$ a conditional-Gaussian random field with mean field ${\displaystyle \varphi _{i}\cdot I\doteq \varphi _{i}\cdot \varphi _{0}\cdot I_{0}}$. The unknown variable to be estimated explicitly by MAP is the mapping of the hyper-template ${\displaystyle \varphi _{0}}$, with the other mappings considered as nuisance or hidden variables which are integrated out via the Bayes procedure. This is accomplished using the expectation–maximization algorithm.

The orbit-model is exploited by associating the unknown to be estimated flows to their log-coordinates ${\displaystyle v_{i},i=1,\dots }$ via the Riemannian geodesic log and exponential for computational anatomy the initial vector field in the tangent space at the identity so that ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{i})\doteq \varphi _{i}}$, with ${\displaystyle \operatorname {Exp} _{\mathrm {id} }(v_{0})}$ the mapping of the hyper-template. The MAP estimation problem becomes

${\displaystyle \max _{v_{0}}p(I^{D},\theta =v_{0})=\int p(I^{D},\theta =v_{0}\mid v_{1},v_{2},\dots )\pi (v_{1},v_{2},\dots )\,dv}$

The EM algorithm takes as complete data the vector-field coordinates parameterizing the mapping, ${\displaystyle v_{i},i=1,\dots }$ and compute iteratively the conditional-expectation

${\displaystyle {\begin{cases}Q(\theta =v_{0};\theta ^{\text{old}}=v_{0}^{\text{old}})&=-\operatorname {E} (\log p(I^{D},\theta =v_{0}\mid v_{1},v_{2},\dots )\mid I^{D},\theta ^{\text{old}})\\&=-\|({\bar {I}}^{\text{old}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0})^{-1}){\sqrt {\beta ^{\text{old}}}}\|^{2}-\|v_{0}\|_{V}^{2}\end{cases}}}$

• Compute new template maximizing Q-function, setting

${\displaystyle \theta ^{\text{new}}\doteq v_{0}^{\text{new}}=\arg \max _{\theta =v_{0}}Q(\theta ;\theta ^{\text{old}}=v_{0}^{\text{old}})=-\left\|({\bar {I}}^{\text{old}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0})^{-1}){\sqrt {\beta ^{\text{old}}}}\right\|^{2}-\|v_{0}\|_{V}^{2}}$

• Compute the mode-approximation for the expectation updating the expected-values for the mode values:

${\displaystyle v_{i}^{\text{new}}=\arg \max _{v:{\dot {\varphi }}=v\circ \varphi }-\int _{0}^{1}\|v_{t}\|_{V}^{2}\,dt-\|I^{D_{i}}-I_{0}\circ \operatorname {Exp} _{\mathrm {id} }(v_{0}^{\text{old}})^{-1}\circ \operatorname {Exp} _{\mathrm {id} }(v)^{-1}\|^{2}.i=1,2,\dots }$

${\displaystyle \beta ^{\text{new}}(x)=\sum _{i=1}^{n}|D\operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})(x)|,{\text{ with }}{\bar {I}}^{\text{new}}(x)={\frac {\sum _{i=1}^{n}I^{D_{i}}\circ \operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})|D\operatorname {Exp} _{\mathrm {id} }(v_{i}^{\text{new}})(x)|}{\beta ^{\text{old}}(x)}}}$

References

1. Christensen, G.E.; Rabbitt, R.D.; Miller, M.I. (1996-02-01). "Deformable Templates Using Large Deformation Kinematics". IEEE Transactions on Image Processing. 5 (10): 1435–1447. Bibcode:1996ITIP....5.1435C. doi:10.1109/83.536892. PMID 18290061.
2. Ashburner, J. (July 2007). "A fast diffeomorphic image registration algorithm". NeuroImage. 38 (1): 95–113. doi:10.1016/j.neuroimage.2007.07.007. PMID 17761438. S2CID 545830.
3. Avants, B. B.; Epstein, C. L.; Grossman, M.; Gee, J. C. (2008-02-01). "Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain". Medical Image Analysis. 12 (1): 26–41. doi:10.1016/j.media.2007.06.004. ISSN 1361-8423. PMC 2276735. PMID 17659998.
4. Miller, Michael; Banerjee, Ayananshu; Christensen, Gary; Joshi, Sarang; Khaneja, Navin; Grenander, Ulf; Matejic, Larissa (1997-06-01). "Statistical methods in computational anatomy". Statistical Methods in Medical Research. 6 (3): 267–299. doi:10.1177/096228029700600305. PMID 9339500. S2CID 35247542.
5. U. Grenander and M. I. Miller (2007-02-08). Pattern Theory: From Representation to Inference. Oxford University Press. ISBN 9780199297061.
6. M. I. Miller and S. Mori and X. Tang and D. Tward and Y. Zhang (2015-02-14). Bayesian Multiple Atlas Deformable Templates. Brain Mapping: An Encyclopedic Reference. Academic Press. ISBN 9780123973160.
7. Srivastava, S.; Miller, M. I.; Grenander, U. (1997-01-01). Byrnes, Christopher I.; Datta, Biswa N.; Martin, Clyde F.; Gilliam, David S. (eds.). Ergodic Algorithms on Special Euclidean Groups for ATR. Systems & Control: Foundations & Applications. Birkhäuser Boston. pp. 327–350. CiteSeerX 10.1.1.44.4751. doi:10.1007/978-1-4612-4120-1_18. ISBN 978-1-4612-8662-2.
8. ^ P. Dupuis, U. Grenander, M.I. Miller, Existence of Solutions on Flows of Diffeomorphisms, Quarterly of Applied Math, 1997.
9. ^ Trouvé, A. (1995). "Action de groupe de dimension infinie et reconnaissance de formes". Comptes Rendus de l'Académie des Sciences, Série I (in French). 321 (8): 1031–1034.
10. Tang, Xiaoying; Oishi, Kenichi; Faria, Andreia V.; Hillis, Argye E.; Albert, Marilyn S.; Mori, Susumu; Miller, Michael I. (2013-06-18). "Bayesian Parameter Estimation and Segmentation in the Multi-Atlas Random Orbit Model". PLOS ONE. 8 (6): e65591. Bibcode:2013PLoSO...865591T. doi:10.1371/journal.pone.0065591. PMC 3688886. PMID 23824159.

• Bayesian estimation
• Computational anatomy
• Geometry
• Fluid mechanics
• Neural engineering
• Biomedical engineering