Misplaced Pages

Part of a series on
Continuum mechanics
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$Fick's laws of diffusion
Laws Conservations Mass Momentum Energy Inequalities Clausius–Duhem (entropy)
Solid mechanics Deformation Elasticity linear Plasticity Hooke's law Stress Strain Finite strain Infinitesimal strain Compatibility Bending Contact mechanics frictional Material failure theory Fracture mechanics
Fluid mechanics Fluids Statics · Dynamics Archimedes' principle · Bernoulli's principle Navier–Stokes equations Poiseuille equation · Pascal's law Viscosity (Newtonian · non-Newtonian) Buoyancy · Mixing · Pressure Liquids Adhesion Capillary action Chromatography Cohesion (chemistry) Surface tension Gases Atmosphere Boyle's law Charles's law Combined gas law Fick's law Gay-Lussac's law Graham's law Plasma
Rheology Viscoelasticity Rheometry Rheometer Smart fluids Electrorheological Magnetorheological Ferrofluids
Scientists Bernoulli Boyle Cauchy Charles Euler Fick Gay-Lussac Graham Hooke Newton Navier Noll Pascal Stokes Truesdell
v t e

Bearing pressure is a particular case of contact mechanics often occurring in cases where a convex surface (male cylinder or sphere) contacts a concave surface (female cylinder or sphere: bore or hemispherical cup). Excessive contact pressure can lead to a typical bearing failure such as a plastic deformation similar to peening. This problem is also referred to as bearing resistance.

Hypotheses

A contact between a male part (convex) and a female part (concave) is considered when the radii of curvature are close to one another. There is no tightening and the joint slides with no friction therefore, the contact forces are normal to the tangent of the contact surface.

Moreover, bearing pressure is restricted to the case where the charge can be described by a radial force pointing towards the center of the joint.

Case of a cylinder-cylinder contact

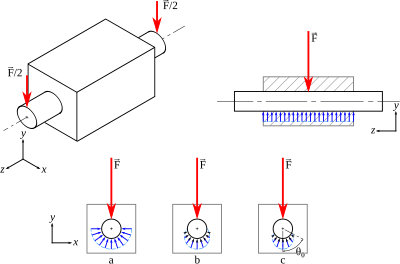
In the case of a revolute joint or of a hinge joint, there is a contact between a male cylinder and a female cylinder. The complexity depends on the situation, and three cases are distinguished:

• the clearance is negligible:
  • a) the parts are rigid bodies,
  • b) the parts are elastic bodies;
• c) the clearance cannot be ignored and the parts are elastic bodies.

By "negligible clearance", H7/g6 fit is typically meant.

The axes of the cylinders are along the z-axis, and two external forces apply to the male cylinder:

• a force ${\displaystyle {\vec {F}}}$ along the y-axis, the load;
• the action of the bore (contact pressure).

The main concern is the contact pressure with the bore, which is uniformly distributed along the z-axis.

Notation:

• D is the nominal diameter of both male and female cylinders;
• L the guiding length.

Negligible clearance and rigid bodies

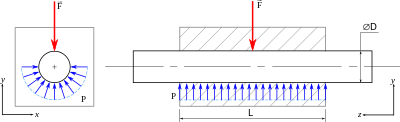
In this first modeling, the pressure is uniform. It is equal to:

${\displaystyle P={\frac {F}{D\times L}}={\frac {\mathrm {radial\ load} }{\mathrm {projected\ area} }}}$.

There are two ways to obtain this result.

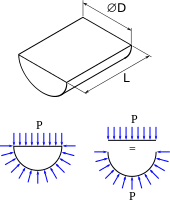
First, we can consider a hemicylinder in a fluid, with a uniform hydrostatic pressure. The equilibrium is achieved when the resulting force on the flat surface is equal to the resulting force on the curved one. The flat surface is a D × L rectangle, therefore

F = P × (D × L)

q.e.d.

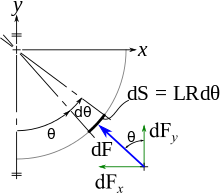
Second, we can integrate the pressure elementary forces. Consider a small surface dS on the cylindrical part, parallel to a generating line; its length is L, and it is bound by the angles θ and θ + dθ. This small surface element can be considered as a flat rectangle which dimensions are L × (dθ × D/2). The pressure force on the surface is equal to

dF = P × dS = ⁠1/2⁠ × P × D × L × dθ

The (y, z) plane is a plane of reflection symmetry, so the x compound of this force is annihilated by the force on the symmetrical surface element. The y compound of this force is equal to:

dF_y = cos(θ) dF = ⁠1/2⁠ × cos(θ) × P × D × L × dθ.

The resulting force is equal to

${\displaystyle F_{y}=\int _{-\pi /2}^{\pi /2}{\frac {1}{2}}\times P\times D\times L\times \cos(\theta )\times \mathrm {d} \theta ={\frac {1}{2}}\times P\times D\times L\times \left_{-\pi /2}^{\pi /2}=P\times D\times L}$

q.e.d.

This calculation is similar to the case of a cylindrical vessel under pressure.

Negligible clearance and elastic bodies

If it is considered that the parts deform elastically, then the contact pressure is no longer uniform and transforms to a sinusoidal repartition:

P(θ) = P_max⋅cos θ

with

${\displaystyle P_{\mathrm {max} }={\frac {4}{\pi }}\cdot {\frac {F}{LD}}}$.

This is a particular case of the following section (θ₀ = π/2).

The maximum pressure is 4/π ≃ 1.27 times bigger than the case of uniform pressure.

Clearance and elastic bodies

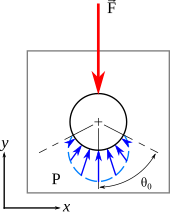
In cases where the clearance can not be neglected, the contact between the male part is no longer the whole half-cylinder surface but is limited to a 2θ₀ angle. The pressure follows Hooke's law:

P(θ) = K⋅δ(θ)

where

• K is a positive real number that represents the rigidity of the materials;
• δ(θ) is the radial displacement of the contact point at the angle θ;
• α is a coefficient that represents the behaviour of the material:
  • α = 1 for metals (purely elastic behaviour),
  • α > 1 for polymers (viscoelastic or viscoplastic behaviour).

The pressure varies as:

A⋅cos θ - B

where A and B are positive real number. The maximum pressure is:

${\displaystyle P_{\mathrm {max} }={\frac {4F}{LD}}\times {\frac {1-\cos \theta _{0}}{2\theta _{0}-\sin 2\theta _{0}}}}$

the angle θ₀ is in radians.

The rigidity coefficient K and the half contact angle θ₀ can not be derived from the theory. They must be measured. For a given system — given diameters and materials —, thus for given K and clearance j values, it is possible to obtain a curve θ₀ = ƒ(F/(DL)).

Relationship between pressure, clearance and contact angle

The part no. 1 is the containing cylinder (female, concave), the part no. 2 is the contained cylinder (male, convex); the center of the cylinder i is O_i, and its radius is R_i.

The reference position is an ideal situation where both cylinders are concentric. The clearing, expressed as a radius (not diameter), is:

j = R₁ - R₂.

Under the load, the part 2 gets in contact with the part 1, the he surfaces deform. we suppose that the cylinder 2 is rigid (no deformation), and that the cylinder 1 is an elastic body. The indentation of 2 into 1 has a depth of δ_max; the cylinder movement is e (excentration):

e = O₁O₂ = j + δ_max.

We considere the frame at the center of the cylinder 1 (O₁, x, y). Let M be a point on the contact surface; θ is the angle (-y, O₁M). The displacement of the surface, δ, is:

δ(θ) = O₁M - R₁.

with δ(0) = δ_max. The coordinates of M are:

M((R₁ + δ(θ)⋅sin θ) ; -(R₁ + δ(θ))⋅cos θ)

and the coordinates of O₂:

O₂(0 ; -e).

Consider the frame (O₁, u, v), where the axis u is (O₁M). In this frame, the coordinates are:

M(R₁ + δ(θ) ; 0)

O₂(e⋅cos θ ; -e⋅sin θ)

We know that

${\displaystyle {\overrightarrow {O_{1}M}}={\overrightarrow {O_{1}O_{2}}}+{\overrightarrow {O_{2}M}}}$

thus

${\displaystyle \left\{{\begin{aligned}R_{1}+\delta (\theta )&=&e\cdot \cos \theta +R_{2}\cos \varphi \\0&=&-e\cdot \sin \theta +R_{2}\sin \varphi \end{aligned}}\right.}$

then we use the expression of e and R₁ = j + R₂:

${\displaystyle \left\{{\begin{aligned}j+R_{2}+\delta (\theta )&=&(j+\delta _{\max })\cdot \cos \theta +R_{2}\cos \varphi \\0&=&-(j+\delta _{\max })\cdot \sin \theta +R_{2}\sin \varphi \end{aligned}}\right.}$

The deformations are small, as we are in the elastic domain. Thus, δ_max ≪ R₁ and therefore |φ| ≪ 1, i.e.

cos φ ≃ 1

sin φ ≃ φ (in radians)

thus

${\displaystyle \left\{{\begin{aligned}(j+\delta _{\max })\cdot \cos \theta +R_{2}-(j+R_{2}+\delta (\theta ))&=&0\\(j+\delta _{\max })\cdot \sin \theta -R_{2}\cdot \varphi &=&0\end{aligned}}\right.}$

and

${\displaystyle \left\{{\begin{aligned}(j+\delta _{\max })\cdot \cos \theta -j-\delta (\theta )&=&0\\(j+\delta _{\max })\cdot \sin \theta -R_{2}\cdot \varphi &=&0\end{aligned}}\right.}$

At θ = θ₀, δ(0) = 0 and the first equation is

${\displaystyle (j+\delta _{\max })\cdot \cos \theta _{0}-j=0\Rightarrow \delta _{\max }={\frac {j(1-\cos \theta _{0})}{\cos \theta _{0}}}\Leftrightarrow \cos \theta _{0}={\frac {j}{j+\delta _{\max }}}}$

and thus

${\displaystyle \left(j+{\frac {j(1-\cos \theta _{0})}{\cos \theta _{0}}}\right)\cdot \cos \theta -j-\delta (\theta )=0}$

${\displaystyle \Longrightarrow \delta (\theta )=j\left({\frac {\cos \theta }{\cos \theta _{0}}}-1\right)}$ .

If we use the law of elasticity for a metal (α = 1):

${\displaystyle \left\{{\begin{aligned}P(\theta )&=&K\cdot j\left({\frac {\cos \theta }{\cos \theta _{0}}}-1\right)\\P_{\max }&=&K\cdot j\cdot {\frac {1-\cos \theta _{0}}{\cos \theta _{0}}}\end{aligned}}\right.}$

The pressure is an affine function of cos θ:

P(θ) = A⋅cos θ - B

with A = K⋅j/cos θ₀ and B = A⋅cos θ₀.

Case where the clearance can be neglected

If j ≃ 0 (R₁ ≃ R₂), then the contact is on the whole half-perimeter: 2θ₀ ≃ π and cos θ₀ ≃ 0. The value of 1/cos θ₀ rise towards infinity, thus

${\displaystyle \delta (\theta )\simeq j{\frac {\cos \theta }{\cos \theta _{0}}}}$

As j and cos θ₀ both tend towards 0, the ratio j/cos θ₀ is not defined when j goes to 0. In mechanical engineering, j = 0 is an uncertain fit, it is a nonsense, both mathematically and mechanically. We are looking for a limit function

${\displaystyle P_{\pi /2}(\theta )=\lim _{\theta _{0}\to \pi /2}P_{\theta _{0}}(\theta )}$.

So, the pressure is a sinusoid function of θ:

${\displaystyle P(\theta )=K\cdot {\frac {j}{\cos \theta _{0}}}\cdot \cos \theta }$

thus

P(θ) = P_max⋅cos θ

with

${\displaystyle P_{\max }=K\cdot {\frac {j}{\cos \theta _{0}}}}$.

Consider an infinitesimal element of surface dS bound by θ and θ + dθ. As in the case of the uniform pressure, we have

dF_y(θ) = cos(θ)dF = ⁠1/2⁠ × cos(θ) × P(θ) × D × L × dθ = ⁠1/2⁠ × cos(θ) × P_max × D × L × dθ.

When we integrate between -π/2 and π/2, the result is:

${\displaystyle F=\int _{-\pi /2}^{\pi /2}\mathrm {d} F_{y}(\theta )\mathrm {d} \theta ={\frac {1}{2}}P_{\max }DL\int _{-\pi /2}^{\pi /2}\cos ^{2}\theta \mathrm {d} \theta }$

We know that (e.g. using the Euler's formula):

${\displaystyle \int _{-\pi /2}^{\pi /2}\cos ^{2}\theta \mathrm {d} \theta ={\frac {1}{4}}\left_{-\pi /2}^{\pi /2}={\frac {1}{2}}\left_{-\pi /2}^{\pi /2}={\frac {\pi }{2}}}$

therefore

${\displaystyle F={\frac {\pi }{4}}P_{\max }DL}$

and thus

${\displaystyle P_{\max }={\frac {4}{\pi }}{\frac {F}{DL}}}$

q.e.d.

Case where the clearance can not be neglected

The force on an infinitesimal element of surface is:

dF(θ) = P(θ)dS = Kδ(θ)dS = ⁠1/2⁠ × K × j × cos θ/cos θ₀ - 1) × dS

${\displaystyle \mathrm {d} F_{y}={\frac {Kj}{2}}\left({\frac {\cos \theta }{\cos \theta _{0}}}-1\right)DL\cos \theta \mathrm {d} \theta }$

${\displaystyle F={\frac {KjDL}{2}}\int _{-\theta _{0}}^{\theta _{0}}\left({\frac {\cos ^{2}\theta }{\cos \theta _{0}}}-\cos \theta \right)\mathrm {d} \theta ={\frac {KjDL}{2}}\left_{-\theta _{0}}^{\theta _{0}}}$

thus

${\displaystyle F={\frac {KjDL}{2}}\left({\frac {2\theta _{0}+2\sin \theta _{0}\cos \theta _{0}}{2\cos \theta _{0}}}-2\sin \theta _{0}\right)={\frac {KjDL}{2}}\left({\frac {\theta _{0}-\sin \theta _{0}\cos \theta _{0}}{\cos \theta _{0}}}\right)}$.

We recognise the trigonometric identity sin 2θ = 2 sin θ cos θ :

${\displaystyle F={\frac {KjDL}{4\cos \theta _{0}}}(2\theta _{0}-\sin 2\theta _{0})}$

thus

${\displaystyle K={\frac {4F\cos \theta _{0}}{jDL(2\theta _{0}-\sin 2\theta _{0})}}}$

and therefore:

${\displaystyle P_{\max }=Kj{\frac {1-\cos \theta _{0}}{\cos \theta _{0}}}={\frac {4F}{DL}}\times {\frac {1-\cos \theta _{0}}{2\theta _{0}-\sin 2\theta _{0}}}}$

q.e.d.

Case of a sphere-sphere contact

A sphere-sphere contact corresponds to a spherical joint (socket/ball), such as a ball jointed cylinder saddle. It can also describe the situation of bearing balls.

Case of uniform pressure

The case is similar as above: when the parts are considered as rigid bodies and the clearance can be neglected, then the pressure is supposed to be uniform. It can also be calculated considering the projected area:

${\displaystyle P={\frac {F}{\pi R^{2}}}={\frac {\mathrm {radial\ load} }{\mathrm {projected\ area} }}}$.

Case of a sinusoidal repartition of pressure

As in the case of cylinder-cylinder contact, when the parts are modeled as elastic bodies with a negligible clearance, then the pressure can be modeled with a sinusoidal repartition:

P(θ, φ) = P_max⋅cos θ

with

${\displaystyle P={\frac {3}{2}}\cdot {\frac {F}{\pi R^{2}}}}$.

Hertz contact stress

When the clearance can not be neglected, it is then necessary to know the value of the half contact angle θ₀ , which can not be determined in a simple way and must be measured. When this value is not available, the Hertz contact theory can be used.

The Hertz theory is normally only valid when the surfaces can not conform, or in other terms, can not fit each other by elastic deformation; one surface must be convex, the other one must be also convex plane. This is not the case here, as the outer cylinder is concave, so the results must be considered with great care. The approximation is only valid when the inner radius of the container R₁ is far greater than the outer radius of the content R₂, in which case the surface container is then seen as flat by the content. However, in all cases, the pressure that is calculated with the Hertz theory is greater than the actual pressure (because the contact surface of the model is smaller than the real contact surface), which affords designers with a safety margin for their design.

In this theory, the radius of the female part (concave) is negative.

A relative diameter of curvature is defined:

${\displaystyle {\frac {1}{d^{*}}}={\frac {1}{d_{1}}}+{\frac {1}{d_{2}}}}$

where d₁ is the diameter of the female part (negative) and d₂ is the diameter of the male part (positive). An equivalent module of elasticity is also defined:

${\displaystyle {\frac {1}{E^{*}}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}}$

where ν_i is the Poisson's ratio of the material of the part i and E_i its Young's modulus.

For a cylinder-cylinder contact, the width of the contact surface is:

${\displaystyle b=\left({\frac {2F}{\pi L}}\cdot {\frac {d^{*}}{E^{*}}}\right)^{1/2}}$

and the maximal pressure is in the middle:

${\displaystyle P_{\max }={\frac {2F}{\pi bL}}={\sqrt {\frac {2FE^{*}}{\pi Ld^{*}}}}}$.

In case of a sphere-sphere contact, the contact surface is a disk whose radius is:

${\displaystyle a=\left({\frac {3F}{8}}\cdot {\frac {d^{*}}{E^{*}}}\right)^{1/3}}$

and the maximal pressure is in the middle:

${\displaystyle P_{\max }={\frac {3F}{\pi a^{2}}}={\frac {4}{\pi }}{\sqrt{3F\left({\frac {E^{*}}{d^{*}}}\right)^{2}}}}$.

Applications

Bolt used as a stop

In a bolted connection, the role of the bolts is normally to press one parts on the other; the adherence (friction) is opposed to the tangent forces and prevents the parts from sliding apart. In some cases however, the adherence is not sufficient. The bolts then play the role of stops: the screws endure shear stress whereas the hole endure bearing pressure.

In order to increase the bearing pressure of a material, there are several factors that can be considered. One of the most effective methods is to increase the surface area of the material. By increasing the surface area, the load is distributed over a larger area, reducing the bearing pressure.

In good design practice, the threaded part of the screw should be small and only the smooth part should be in contact with the plates; in the case of a shoulder screw, the clearance between the screw and the hole is very small ( a case of rigid bodies with negligible clearance). If the acceptable pressure limit P_lim of the material is known, the thickness t of the part and the diameter d of the screw, then the maximum acceptable tangent force for one bolt F_{b, Rd} (design bearing resistance per bolt) is:

F_{b, Rd} = P_lim × d × t.

In this case, the acceptable pressure limit is calculated from the ultimate tensile stress f_u and factors of safety, according to the Eurocode 3 standard. In the case of two plates with a single overlap and one row of bolts, the formula is:

P_lim = 1.5 × f_u/γ_M2

where

• γ_M2 = 1.25: partial safety factor.

In more complex situations, the formula is:

P_lim = k₁ × α × f_u/γ_M2

where

• k₁ and α are factors that take into account other failure modes than the bearing pressure overload; k₁ take into account the effects that are perpendicular to the tangent force, and α the effects along the force;
• k₁ = min{2.8e₂/d₀ ; 2.5} for end bolts,
  k₁ = min{1.4p₂/d₀ ; 2.5} for inner bolts,
  • e₂: edge distance from the centre of a fastener hole to the adjacent edge of the part, measured at right angles to the direction of load transfer,
  • p₂: spacing measured perpendicular to the load transfer direction between adjacent lines of

fasteners,

• • d₀: diameter of the passthrough hole;
• α = min{e₁/3d₀ ; p₁/3d₀ - 1/4 ; f_ub/f_u ; 1}, with
  • e₁: end distance from the center of a fastener hole to the adjacent end of the part, measured in the direction of load transfer,
  • p₁: spacing between centers of fasteners in the direction of load transfer,
  • f_ub: specified ultimate tensile strength of the bolt.

When the parts are in wood, the acceptable limit pressure is about 4 to 8.5 MPa.

Plain bearing

In plain bearings, the shaft is usually in contact with a bushing (sleeve or flanged) to reduce friction. When the rotation is slow and the load is radial, the model of uniform pressure can be used (small deformations and clearance).

The product of the bearing pressure times the circumferential sliding speed, called load factor PV, is an estimation of the resistance capacity of the material against the frictional heating.

References

1. ^ EN 1993-1-8:2005 Eurocode 3: Design of steel structures - Part 1-8: Design of joints
2. due to the clearance, the diameter of the bore is bigger than the diameter of the male cylinder; however, we suppose that the diameters are close to each othert
3. ^ SG 2003, p. 139
4. GCM 2000, p. 177
5. Aublin 1992, pp. 108, 136
6. ^ SG 2003, p. 140
7. Aublin 1992, pp. 120–122, 136–137
8. Budynas, Richard G.; Nisbett, J. Keith; Shigley, Joseph Edward (2011). Shigley's mechanical engineering design (9th ed.). New York: McGraw-Hill. pp. 664, eq. 12-31. ISBN 978-0-07-352928-8. OCLC 436031178.
9. Aublin 1992, pp. 120–122, 137–138
10. GCM 2000, pp. 110–111
11. Aublin 1992, pp. 108, 144–145
12. Aublin 1992, pp. 120–122, 145–150
13. Fanchon 2001, pp. 467–471
14. ^ Seinturier, Francine. "C-viii Assemblages boulonnés". Construction métallique 2 (PDF) (in French). IUT Grenoble I. Archived from the original (PDF) on 2011-11-25. Retrieved 2015-12-04.
15. MB (April 2007). "Assemblages". Wiki de l'Unité Construction de Gramme (in French). Archived from the original on 2015-11-25. Retrieved 2015-11-25.
16. Fanchon 2011, p. 255
17. Chevalier 2004, p. 258
18. GCM 2000, pp. 113–116, 176–181
19. L.P. Pierre et Marie Curie, Aulnoye. "Paliers lisses ou coussinets". Construction mécanique (PDF) (in French). Université de Toulon.

Bibliography

• Aublin, Michel; Boncompain, René; Boulaton, Michel; Caron, Daniel; Jeay, Émile; Lacage, Bernard; Réa, Jacky (1992). Systèmes mécaniques : théorie et dimensionnement (in French). Dunod. pp. 108–157. ISBN 2-10-001051-4.
• Chevalier, André (2004). Guide du dessinateur industriel (in French). Hachette technique. p. 258. ISBN 978-2-01-168831-6.
• Fanchon, Jean-Louis (2001). Guide de mécanique : sciences et technologies industrielles (in French). Nathan. pp. 467–471. ISBN 978-2-09-178965-1.
• Fanchon, Jean-Louis (2011). "Calcul des coussinets (régime non hydrodynamique)". Guide des sciences et technologies industrielles (in French). Afnor/Nathan. pp. 255–256. ISBN 978-2-09-161590-5.
• Texeido, C.; Jouanne, J.-C.; Bauwe, B.; Chambraud, P.; Ignatio, G.; Guérin, C. (2000). Guide de construction mécanique (in French). Delagrave. pp. 110–116, 176–180. ISBN 978-2-206-08224-0.
• Spenlé, D.; Gourhant, R. (2003). Guide du calcul en mécanique : maîtriser la performance des systèmes industriels (in French). Hachette technique. pp. 139–140. ISBN 2-01-16-8835-3.

• Bearings (mechanical)
• Mechanical engineering
• Solid mechanics