Misplaced Pages

Benktander type II distribution

Probability density function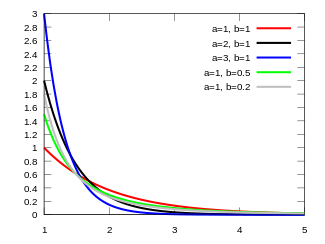
Cumulative distribution function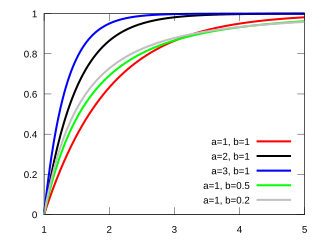
Parameters	${\displaystyle a>0}$ (real) ${\displaystyle 0<b\leq 1}$ (real)
Support	${\displaystyle x\geq 1}$
PDF	${\displaystyle e^{{\frac {a}{b}}(1-x^{b})}x^{b-2}\left(ax^{b}-b+1\right)}$
CDF	${\displaystyle 1-x^{b-1}e^{{\frac {a}{b}}(1-x^{b})}}$
Mean	${\displaystyle 1+{\frac {1}{a}}}$
Median	${\displaystyle {\begin{cases}{\frac {\log(2)}{a}}+1&{\text{if}}\ b=1\\\left(\left({\frac {1-b}{a}}\right)\mathbf {W} \left({\frac {2^{\frac {b}{1-b}}ae^{\frac {a}{1-b}}}{1-b}}\right)\right)^{\tfrac {1}{b}}&{\text{otherwise}}\ \end{cases}}}$ Where ${\displaystyle \mathbf {W} (x)}$ is the Lambert W function
Mode	${\displaystyle 1}$
Variance	${\displaystyle {\frac {-b+2ae^{\frac {a}{b}}\mathbf {E} _{1-{\frac {1}{b}}}\left({\frac {a}{b}}\right)}{a^{2}b}}}$ Where ${\displaystyle \mathbf {E} _{n}(x)}$ is the generalized Exponential integral

The Benktander type II distribution, also called the Benktander distribution of the second kind, is one of two distributions introduced by Gunnar Benktander (1970) to model heavy-tailed losses commonly found in non-life/casualty actuarial science, using various forms of mean excess functions (Benktander & Segerdahl 1960). This distribution is "close" to the Weibull distribution (Kleiber & Kotz 2003).

See also

• Weibull distribution
• Benktander type I distribution

Notes

1. ^ From Wolfram Alpha

References

• Kleiber, Christian; Kotz, Samuel (2003). "7.4 Benktander Distributions". Statistical Size Distributions in Economics and Actuarial Science. Wiley Series and Probability and Statistics. John Wiley & Sons. pp. 247–250. ISBN 9780471457169.
• Benktander, Gunnar; Segerdahl, Carl-Otto (1960). "On the Analytical Representation of Claim Distributions with Special Reference to Excess of Loss Reinsurance". Proceedings of the XVIth International Congress of Actuaries, Brussels, 1960: 626–646.
• Benktander, Gunnar (1970). "Schadenverteilungen nach Grösse in der Nicht-Lebensversicherung" [Loss Distributions by Size in Non-life Insurance]. Bulletin of the Swiss Association of Actuaries (in German): 263–283.

• Continuous distributions