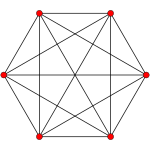
 5-simplex |
 Cantellated 5-simplex |
 Bicantellated 5-simplex |
 Birectified 5-simplex |
 Cantitruncated 5-simplex |
 Bicantitruncated 5-simplex |
| Orthogonal projections in A5 Coxeter plane | ||
|---|---|---|
In five-dimensional geometry, a cantellated 5-simplex is a convex uniform 5-polytope, being a cantellation of the regular 5-simplex.
There are unique 4 degrees of cantellation for the 5-simplex, including truncations.
Cantellated 5-simplex
| Cantellated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | rr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 27 | 6 r{3,3,3} 6 rr{3,3,3} 15 {}x{3,3} |
| Cells | 135 | 30 {3,3} 30 r{3,3} 15 rr{3,3} 60 {}x{3} |
| Faces | 290 | 200 {3} 90 {4} |
| Edges | 240 | |
| Vertices | 60 | |
| Vertex figure |  Tetrahedral prism | |
| Coxeter group | A5 , order 720 | |
| Properties | convex | |
The cantellated 5-simplex has 60 vertices, 240 edges, 290 faces (200 triangles and 90 squares), 135 cells (30 tetrahedra, 30 octahedra, 15 cuboctahedra and 60 triangular prisms), and 27 4-faces (6 cantellated 5-cell, 6 rectified 5-cells, and 15 tetrahedral prisms).
Alternate names
- Cantellated hexateron
- Small rhombated hexateron (Acronym: sarx) (Jonathan Bowers)
Coordinates
The vertices of the cantellated 5-simplex can be most simply constructed on a hyperplane in 6-space as permutations of (0,0,0,1,1,2) or of (0,1,1,2,2,2). These represent positive orthant facets of the cantellated hexacross and bicantellated hexeract respectively.
Images
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | ||
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry |
Bicantellated 5-simplex
| Bicantellated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | 2rr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 32 | 12 t02{3,3,3} 20 {3}x{3} |
| Cells | 180 | 30 t1{3,3} 120 {}x{3} 30 t02{3,3} |
| Faces | 420 | 240 {3} 180 {4} |
| Edges | 360 | |
| Vertices | 90 | |
| Vertex figure | 
| |
| Coxeter group | A5×2, ], order 1440 | |
| Properties | convex, isogonal | |
Alternate names
- Bicantellated hexateron
- Small birhombated dodecateron (Acronym: sibrid) (Jonathan Bowers)
Coordinates
The coordinates can be made in 6-space, as 90 permutations of:
- (0,0,1,1,2,2)
This construction exists as one of 64 orthant facets of the bicantellated 6-orthoplex.
Images
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | ]= | |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | ]= |
Cantitruncated 5-simplex
| cantitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | tr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 27 | 6 t012{3,3,3} 6 t{3,3,3} 15 {}x{3,3} |
| Cells | 135 | 15 t012{3,3} 30 t{3,3} 60 {}x{3} 30 {3,3} |
| Faces | 290 | 120 {3} 80 {6} 90 {}x{} |
| Edges | 300 | |
| Vertices | 120 | |
| Vertex figure | 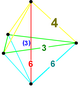 Irr. 5-cell | |
| Coxeter group | A5 , order 720 | |
| Properties | convex | |
Alternate names
- Cantitruncated hexateron
- Great rhombated hexateron (Acronym: garx) (Jonathan Bowers)
Coordinates
The vertices of the cantitruncated 5-simplex can be most simply constructed on a hyperplane in 6-space as permutations of (0,0,0,1,2,3) or of (0,1,2,3,3,3). These construction can be seen as facets of the cantitruncated 6-orthoplex or bicantitruncated 6-cube respectively.
Images
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | ||
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry |
Bicantitruncated 5-simplex
| Bicantitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | 2tr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 32 | 12 tr{3,3,3} 20 {3}x{3} |
| Cells | 180 | 30 t{3,3} 120 {}x{3} 30 t{3,4} |
| Faces | 420 | 240 {3} 180 {4} |
| Edges | 450 | |
| Vertices | 180 | |
| Vertex figure | 
| |
| Coxeter group | A5×2, ], order 1440 | |
| Properties | convex, isogonal | |
Alternate names
- Bicantitruncated hexateron
- Great birhombated dodecateron (Acronym: gibrid) (Jonathan Bowers)
Coordinates
The coordinates can be made in 6-space, as 180 permutations of:
- (0,0,1,2,3,3)
This construction exists as one of 64 orthant facets of the bicantitruncated 6-orthoplex.
Images
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|
|
| Dihedral symmetry | ]= | |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|
|
| Dihedral symmetry | ]= |
Related uniform 5-polytopes
The cantellated 5-simplex is one of 19 uniform 5-polytopes based on the Coxeter group, all shown here in A5 Coxeter plane orthographic projections. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)
| A5 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 t0 |
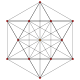 t1 |
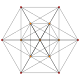 t2 |
 t0,1 |
 t0,2 |
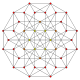 t1,2 |
 t0,3 | |||||
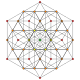 t1,3 |
 t0,4 |
 t0,1,2 |
 t0,1,3 |
 t0,2,3 |
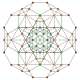 t1,2,3 |
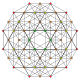 t0,1,4 | |||||
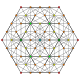 t0,2,4 |
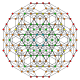 t0,1,2,3 |
 t0,1,2,4 |
 t0,1,3,4 |
 t0,1,2,3,4 | |||||||
Notes
- Klitizing, (x3o3x3o3o - sarx)
- Klitizing, (o3x3o3x3o - sibrid)
- Klitizing, (x3x3x3o3o - garx)
- Klitizing, (o3x3x3x3o - gibrid)
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I,
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II,
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "5D uniform polytopes (polytera)". x3o3x3o3o - sarx, o3x3o3x3o - sibrid, x3x3x3o3o - garx, o3x3x3x3o - gibrid
External links
- Glossary for hyperspace, George Olshevsky.
- Polytopes of Various Dimensions, Jonathan Bowers
- Multi-dimensional Glossary
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||



