Misplaced Pages

Blake canonical form

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Blake–Poretsky law) Standard form of Boolean function

Karnaugh map of AB + BC + AC, a sum of all prime implicants (each rendered in a different color). Deleting AC results in a minimal sum.
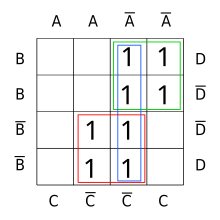
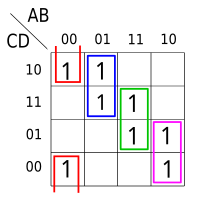ABD + ABC + ABD + ABC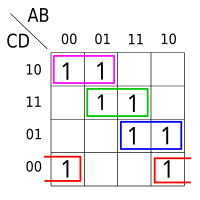ACD + BCD + ACD + BCDBoolean function with two different minimal forms. The Blake canonical form is the sum of the two.

In Boolean logic, a formula for a Boolean function f is in Blake canonical form (BCF), also called the complete sum of prime implicants, the complete sum, or the disjunctive prime form, when it is a disjunction of all the prime implicants of f.

Relation to other forms

The Blake canonical form is a special case of disjunctive normal form.

The Blake canonical form is not necessarily minimal (upper diagram), however all the terms of a minimal sum are contained in the Blake canonical form. On the other hand, the Blake canonical form is a canonical form, that is, it is unique up to reordering, whereas there can be multiple minimal forms (lower diagram). Selecting a minimal sum from a Blake canonical form amounts in general to solving the set cover problem, so is NP-hard.

History

Archie Blake presented his canonical form at a meeting of the American Mathematical Society in 1932, and in his 1937 dissertation. He called it the "simplified canonical form"; it was named the "Blake canonical form" by Frank Markham Brown [d] and Sergiu Rudeanu [d] in 1986–1990. Together with Platon Poretsky's work it is also referred to as "Blake–Poretsky laws".

Methods for calculation

Blake discussed three methods for calculating the canonical form: exhaustion of implicants, iterated consensus, and multiplication. The iterated consensus method was rediscovered by Edward W. Samson and Burton E. Mills, Willard Quine, and Kurt Bing. In 2022, Milan Mossé, Harry Sha, and Li-Yang Tan discovered a near-optimal algorithm for computing the Blake canonical form of a formula in conjunctive normal form.

See also

References

  1. ^ Brown, Frank Markham (2012) . "Chapter 3: The Blake Canonical Form". Boolean Reasoning - The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York: Dover Publications, Inc. pp. 4, 77ff, 81. ISBN 978-0-486-42785-0.
  2. Sasao, Tsutomu (1996). "Ternary Decision Diagrams and their Applications". In Sasao, Tsutomu; Fujita, Masahira (eds.). Representations of Discrete Functions. p. 278. doi:10.1007/978-1-4613-1385-4_12. ISBN 978-0792397205.
  3. ^ Kandel, Abraham (1998). Foundations of Digital Logic Design. World Scientific. p. 177. ISBN 978-9-81023110-1.
  4. Knuth, Donald Ervin (2011). Combinatorial Algorithms, Part 1. The Art of Computer Programming. Vol. 4A. p. 54.
  5. Feldman, Vitaly (2009). "Hardness of Approximate Two-Level Logic Minimization and PAC Learning with Membership Queries". Journal of Computer and System Sciences. 75: 13–25 . doi:10.1016/j.jcss.2008.07.007.
  6. Gimpel, James F. (1965). "A Method for Producing a Boolean Function Having an Arbitrary Prescribed Prime Implicant Table". IEEE Transactions on Computers. 14: 485–488.
  7. Paul, Wolfgang Jakob (1974). "Boolesche Minimalpolynome und Überdeckungsprobleme". Acta Informatica (in German). 4 (4): 321–336. doi:10.1007/BF00289615. S2CID 35973949.
  8. Blake, Archie (November 1932). "Canonical expressions in Boolean algebra". Bulletin of the American Mathematical Society. Abstracts of Papers: 805.
  9. Blake, Archie (1937). Canonical expressions in Boolean algebra (Dissertation). Department of Mathematics, University of Chicago: University of Chicago Libraries.
  10. Blake, Archie (1938). "Canonical expressions in Boolean algebra". The Journal of Symbolic Logic. 3 (2).
  11. Blake, Archie (September 1938). "Corrections to Canonical Expressions in Boolean Algebra". The Journal of Symbolic Logic. 3 (3): 112–113. doi:10.2307/2267595. JSTOR 2267595. S2CID 5810863.
  12. McKinsey, John Charles Chenoweth, ed. (June 1938). "Blake, Archie. Canonical expressions in Boolean algebra, Department of Mathematics, University of Chicago, 1937". The Journal of Symbolic Logic (Review). 3 (2:93): 93. doi:10.2307/2267634. JSTOR 2267634. S2CID 122640691.
  13. Brown, Frank Markham ; Rudeanu, Sergiu (1986), A Functional Approach to the Theory of Prime Implicants, Publication de l'institut mathématique, Nouvelle série, vol. 40, pp. 23–32
  14. Poretsky, Platon Sergeevich (1884). "O sposobach reschenija lopgischeskich rawenstw i ob obrathom spocobe matematischeskoi logiki" О способах решения логических равенств и об обратном способе [On methods of solving logical equalities and the inverse method of mathematical logic. An essay in construction of a complete and accessible theory of deduction on qualitative forms]. Collected Reports of Meetings of Physical and Mathematical Sciences Section of Naturalists' Society of Kazan University (in Russian) (2). (NB. This publication is also referred to as "On methods of solution of logical equalities and on inverse method of mathematical logic".)
  15. Vasyukevich, Vadim O. (2011). "1.10 Venjunctive Properties (Basic Formulae)". Written at Riga, Latvia. Asynchronous Operators of Sequential Logic: Venjunction & Sequention — Digital Circuits Analysis and Design. Lecture Notes in Electrical Engineering (LNEE). Vol. 101 (1 ed.). Berlin / Heidelberg, Germany: Springer-Verlag. p. 20. doi:10.1007/978-3-642-21611-4. ISBN 978-3-642-21610-7. ISSN 1876-1100. LCCN 2011929655. (xiii+1+123+7 pages) (NB. The back cover of this book erroneously states volume 4, whereas it actually is volume 101.)
  16. Samson, Edward Walter; Mills, Burton E. (April 1954). Circuit Minimization: Algebra and Algorithms for New Boolean Canonical Expressions (Technical Report). Bedford, Massachusetts, USA: Air Force Cambridge Research Center. AFCRC TR 54-21.
  17. Quine, Willard Van Orman (November 1955). "A Way to Simplify Truth Functions". The American Mathematical Monthly. 62 (9): 627–631. doi:10.2307/2307285. hdl:10338.dmlcz/142789. JSTOR 2307285.
  18. Bing, Kurt (1955). "On simplifying propositional formulas". Bulletin of the American Mathematical Society. 61: 560.
  19. Bing, Kurt (1956). "On simplifying truth-functional formulas". The Journal of Symbolic Logic. 21 (3): 253–254. doi:10.2307/2269097. JSTOR 2269097. S2CID 37877557.
  20. Mossé, Milan; Sha, Harry; Tan, Li-Yang (2022). "A Generalization of the Satisfiability Coding Lemma and Its Applications". DROPS-IDN/V2/Document/10.4230/LIPIcs.SAT.2022.9. Schloss Dagstuhl – Leibniz-Zentrum für Informatik. doi:10.4230/LIPIcs.SAT.2022.9.
Normal forms in logic
Propositional logic
Predicate logic
Other
Category: