Misplaced Pages

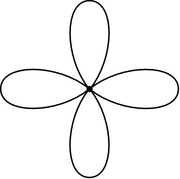
In mathematics, a bouquet graph ${\displaystyle B_{m}}$, for an integer parameter ${\displaystyle m}$, is an undirected graph with one vertex and ${\displaystyle m}$ edges, all of which are self-loops. It is the graph-theoretic analogue of the topological rose, a space of ${\displaystyle m}$ circles joined at a point. When the context of graph theory is clear, it can be called more simply a bouquet.

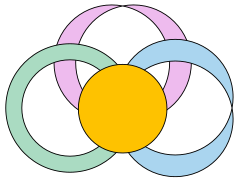
Although bouquets have a very simple structure as graphs, they are of some importance in topological graph theory because their graph embeddings can still be non-trivial. In particular, every cellularly embedded graph can be reduced to an embedded bouquet by a partial duality applied to the edges of any spanning tree of the graph, or alternatively by contracting the edges of any spanning tree.

In graph-theoretic approaches to group theory, every Cayley–Serre graph (a variant of Cayley graphs with doubled edges) can be represented as the covering graph of a bouquet.

References

1. Beineke, Lowell W.; Wilson, Robin J. (2009), Topics in topological graph theory, Encyclopedia of Mathematics and its Applications, vol. 128, Cambridge University Press, Cambridge, p. 5, doi:10.1017/CBO9781139087223, ISBN 978-0-521-80230-7, MR 2581536
2. Ellis-Monaghan, Joanna A.; Moffatt, Iain (2012), "Twisted duality for embedded graphs", Transactions of the American Mathematical Society, 364 (3): 1529–1569, arXiv:0906.5557, doi:10.1090/S0002-9947-2011-05529-7, MR 2869185
3. Sunada, Toshikazu (2013), Topological Crystallography: With a View Towards Discrete Geometric Analysis, Surveys and Tutorials in the Applied Mathematical Sciences, vol. 6, Springer, Tokyo, p. 69, doi:10.1007/978-4-431-54177-6, ISBN 978-4-431-54176-9, MR 3014418

This graph theory-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Parametric families of graphs
• Graph theory stubs