This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
In mathematics, a projection is an idempotent mapping of a set (or other mathematical structure) into a subset (or sub-structure). In this case, idempotent means that projecting twice is the same as projecting once. The restriction to a subspace of a projection is also called a projection, even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane (sheet of paper): the projection of a point is its shadow on the sheet of paper, and the projection (shadow) of a point on the sheet of paper is that point itself (idempotency). The shadow of a three-dimensional sphere is a disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the three-dimensional Euclidean space onto a plane in it, like the shadow example. The two main projections of this kind are:
- The projection from a point onto a plane or central projection: If C is a point, called the center of projection, then the projection of a point P different from C onto a plane that does not contain C is the intersection of the line CP with the plane. The points P such that the line CP is parallel to the plane does not have any image by the projection, but one often says that they project to a point at infinity of the plane (see Projective geometry for a formalization of this terminology). The projection of the point C itself is not defined.
- The projection parallel to a direction D, onto a plane or parallel projection: The image of a point P is the intersection of the plane with the line parallel to D passing through P. See Affine space § Projection for an accurate definition, generalized to any dimension.
The concept of projection in mathematics is a very old one, and most likely has its roots in the phenomenon of the shadows cast by real-world objects on the ground. This rudimentary idea was refined and abstracted, first in a geometric context and later in other branches of mathematics. Over time different versions of the concept developed, but today, in a sufficiently abstract setting, we can unify these variations.
In cartography, a map projection is a map of a part of the surface of the Earth onto a plane, which, in some cases, but not always, is the restriction of a projection in the above meaning. The 3D projections are also at the basis of the theory of perspective.
The need for unifying the two kinds of projections and of defining the image by a central projection of any point different of the center of projection are at the origin of projective geometry.
Definition
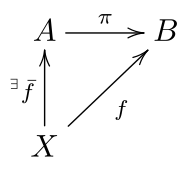
Generally, a mapping where the domain and codomain are the same set (or mathematical structure) is a projection if the mapping is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a right inverse. Both notions are strongly related, as follows. Let p be an idempotent mapping from a set A into itself (thus p ∘ p = p) and B = p(A) be the image of p. If we denote by π the map p viewed as a map from A onto B and by i the injection of B into A (so that p = i ∘ π), then we have π ∘ i = IdB (so that π has a right inverse). Conversely, if π has a right inverse i, then π ∘ i = IdB implies that i ∘ π ∘ i ∘ π = i ∘ IdB ∘ π = i ∘ π; that is, p = i ∘ π is idempotent.
Applications
The original notion of projection has been extended or generalized to various mathematical situations, frequently, but not always, related to geometry, for example:
- In set theory:
- An operation typified by the j- projection map, written projj, that takes an element x = (x1, ..., xj, ..., xn) of the Cartesian product X1 × ⋯ × Xj × ⋯ × Xn to the value projj(x) = xj. This map is always surjective and, when each space Xk has a topology, this map is also continuous and open.
- A mapping that takes an element to its equivalence class under a given equivalence relation is known as the canonical projection.
- The evaluation map sends a function f to the value f(x) for a fixed x. The space of functions Y can be identified with the Cartesian product , and the evaluation map is a projection map from the Cartesian product.
- For relational databases and query languages, the projection is a unary operation written as where is a set of attribute names. The result of such projection is defined as the set that is obtained when all tuples in R are restricted to the set . R is a database-relation.
- In spherical geometry, projection of a sphere upon a plane was used by Ptolemy (~150) in his Planisphaerium. The method is called stereographic projection and uses a plane tangent to a sphere and a pole C diametrically opposite the point of tangency. Any point P on the sphere besides C determines a line CP intersecting the plane at the projected point for P. The correspondence makes the sphere a one-point compactification for the plane when a point at infinity is included to correspond to C, which otherwise has no projection on the plane. A common instance is the complex plane where the compactification corresponds to the Riemann sphere. Alternatively, a hemisphere is frequently projected onto a plane using the gnomonic projection.
- In linear algebra, a linear transformation that remains unchanged if applied twice: p(u) = p(p(u)). In other words, an idempotent operator. For example, the mapping that takes a point (x, y, z) in three dimensions to the point (x, y, 0) is a projection. This type of projection naturally generalizes to any number of dimensions n for the domain and k ≤ n for the codomain of the mapping. See Orthogonal projection, Projection (linear algebra). In the case of orthogonal projections, the space admits a decomposition as a product, and the projection operator is a projection in that sense as well.
- In differential topology, any fiber bundle includes a projection map as part of its definition. Locally at least this map looks like a projection map in the sense of the product topology and is therefore open and surjective.
- In topology, a retraction is a continuous map r: X → X which restricts to the identity map on its image. This satisfies a similar idempotency condition r = r and can be considered a generalization of the projection map. The image of a retraction is called a retract of the original space. A retraction which is homotopic to the identity is known as a deformation retraction. This term is also used in category theory to refer to any split epimorphism.
- The scalar projection (or resolute) of one vector onto another.
- In category theory, the above notion of Cartesian product of sets can be generalized to arbitrary categories. The product of some objects has a canonical projection morphism to each factor. Special cases include the projection from the Cartesian product of sets, the product topology of topological spaces (which is always surjective and open), or from the direct product of groups, etc. Although these morphisms are often epimorphisms and even surjective, they do not have to be.
References
- "Direct product - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
- Lee, John M. (2012). Introduction to Smooth Manifolds. Graduate Texts in Mathematics. Vol. 218 (Second ed.). p. 606. doi:10.1007/978-1-4419-9982-5. ISBN 978-1-4419-9982-5.
Exercise A.32. Suppose are topological spaces. Show that each projection is an open map.
- Brown, Arlen; Pearcy, Carl (1994-12-16). An Introduction to Analysis. Springer Science & Business Media. ISBN 978-0-387-94369-5.
- Alagic, Suad (2012-12-06). Relational Database Technology. Springer Science & Business Media. ISBN 978-1-4612-4922-1.
- Date, C. J. (2006-08-28). The Relational Database Dictionary: A Comprehensive Glossary of Relational Terms and Concepts, with Illustrative Examples. "O'Reilly Media, Inc.". ISBN 978-1-4493-9115-7.
- "Relational Algebra". www.cs.rochester.edu. Archived from the original on 30 January 2004. Retrieved 29 August 2021.
- Sidoli, Nathan; Berggren, J. L. (2007). "The Arabic version of Ptolemy's Planisphere or Flattening the Surface of the Sphere: Text, Translation, Commentary" (PDF). Sciamvs. 8. Retrieved 11 August 2021.
- "Stereographic projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
- "Projection - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
- Roman, Steven (2007-09-20). Advanced Linear Algebra. Springer Science & Business Media. ISBN 978-0-387-72831-5.
- "Retraction - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
- "Product of a family of objects in a category - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-08-11.
Further reading
- Thomas Craig (1882) A Treatise on Projections from University of Michigan Historical Math Collection.
 , and the evaluation map is a projection map from the Cartesian product.
, and the evaluation map is a projection map from the Cartesian product. where
where  is a set of attribute names. The result of such projection is defined as the
is a set of attribute names. The result of such projection is defined as the  . R is a
. R is a  are topological spaces. Show that each projection
are topological spaces. Show that each projection  is an open map.
is an open map.