Misplaced Pages

In set theory, the Schröder–Bernstein theorem states that, if there exist injective functions f : A → B and g : B → A between the sets A and B, then there exists a bijective function h : A → B.

In terms of the cardinality of the two sets, this classically implies that if |A| ≤ |B| and |B| ≤ |A|, then |A| = |B|; that is, A and B are equipotent. This is a useful feature in the ordering of cardinal numbers.

The theorem is named after Felix Bernstein and Ernst Schröder. It is also known as the Cantor–Bernstein theorem or Cantor–Schröder–Bernstein theorem, after Georg Cantor, who first published it (albeit without proof).

Proof

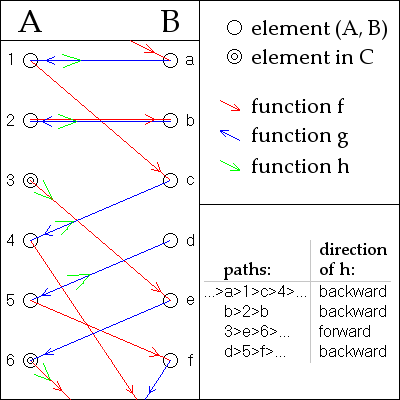
The following proof is attributed to Julius König.

Assume without loss of generality that A and B are disjoint. For any a in A or b in B we can form a unique two-sided sequence of elements that are alternately in A and B, by repeatedly applying ${\displaystyle f}$ and ${\displaystyle g^{-1}}$ to go from A to B and ${\displaystyle g}$ and ${\displaystyle f^{-1}}$ to go from B to A (where defined; the inverses ${\displaystyle f^{-1}}$ and ${\displaystyle g^{-1}}$ are understood as partial functions.)

${\displaystyle \cdots \rightarrow f^{-1}(g^{-1}(a))\rightarrow g^{-1}(a)\rightarrow a\rightarrow f(a)\rightarrow g(f(a))\rightarrow \cdots }$

For any particular a, this sequence may terminate to the left or not, at a point where ${\displaystyle f^{-1}}$ or ${\displaystyle g^{-1}}$ is not defined.

By the fact that ${\displaystyle f}$ and ${\displaystyle g}$ are injective functions, each a in A and b in B is in exactly one such sequence to within identity: if an element occurs in two sequences, all elements to the left and to the right must be the same in both, by the definition of the sequences. Therefore, the sequences form a partition of the (disjoint) union of A and B. Hence it suffices to produce a bijection between the elements of A and B in each of the sequences separately, as follows:

Call a sequence an A-stopper if it stops at an element of A, or a B-stopper if it stops at an element of B. Otherwise, call it doubly infinite if all the elements are distinct or cyclic if it repeats. See the picture for examples.

• For an A-stopper, the function ${\displaystyle f}$ is a bijection between its elements in A and its elements in B.
• For a B-stopper, the function ${\displaystyle g}$ is a bijection between its elements in B and its elements in A.
• For a doubly infinite sequence or a cyclic sequence, either ${\displaystyle f}$ or ${\displaystyle g}$ will do (${\displaystyle g}$ is used in the picture).

Corollary for surjective pair

If we assume the axiom of choice, then a pair of surjective functions ${\displaystyle f}$ and ${\displaystyle g}$ also implies the existence of a bijection. We construct an injective function h : B → A from ${\displaystyle f^{-1}}$ by picking a single element from the inverse image of each point in ${\displaystyle B}$. The surjectivity of ${\displaystyle f}$ guarantees the existence of at least one element in each such inverse image. We do the same to obtain an injective function k : A → B from ${\displaystyle g^{-1}}$. The Schroeder-Bernstein theorem then can be applied to the injections h and k.

Examples

Bijective function from ${\displaystyle \to [0,1)}$

Note: ${\displaystyle [0,1)}$ is the half open set from 0 to 1, including the boundary 0 and excluding the boundary 1.

Let ${\displaystyle f:\to [0,1)}$ with ${\displaystyle f(x)=x/2;}$ and ${\displaystyle g:}$ with ${\displaystyle g(x)=x;}$ the two injective functions.

In line with that procedure ${\displaystyle C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}}$

Then ${\displaystyle h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in \smallsetminus C\end{cases}}}$ is a bijective function from ${\displaystyle \to [0,1)}$.

Bijective function from ${\displaystyle [0,2)\to [0,1)^{2}}$

Let ${\displaystyle f:[0,2)\to [0,1)^{2}}$ with ${\displaystyle f(x)=(x/2;0);}$

Then for ${\displaystyle (x;y)\in [0,1)^{2}}$ one can use the expansions ${\displaystyle x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}}$ and ${\displaystyle y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}}$ with ${\displaystyle a_{k},b_{k}\in \{0,1,...,9\}}$

and now one can set ${\displaystyle g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}}$ which defines an injective function ${\displaystyle [0,1)^{2}\to [0,2)}$. (Example: ${\displaystyle g({\tfrac {1}{3}};{\tfrac {2}{3}})=0.363636...={\tfrac {4}{11}}}$)

And therefore a bijective function ${\displaystyle h}$ can be constructed with the use of ${\displaystyle f(x)}$ and ${\displaystyle g^{-1}(x)}$.

In this case ${\displaystyle C_{0}=[1,2)}$ is still easy but already ${\displaystyle C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})}$ gets quite complicated.

Note: Of course there's a more simple way by using the (already bijective) function definition ${\displaystyle g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}}$. Then ${\displaystyle C}$ would be the empty set and ${\displaystyle h(x)=g_{2}^{-1}(x)}$ for all x.

History

The traditional name "Schröder–Bernstein" is based on two proofs published independently in 1898. Cantor is often added because he first stated the theorem in 1887, while Schröder's name is often omitted because his proof turned out to be flawed while the name of Richard Dedekind, who first proved it, is not connected with the theorem. According to Bernstein, Cantor had suggested the name equivalence theorem (Äquivalenzsatz).

• 1887 Cantor publishes the theorem, however without proof.
• 1887 On July 11, Dedekind proves the theorem (not relying on the axiom of choice) but neither publishes his proof nor tells Cantor about it. Ernst Zermelo discovered Dedekind's proof and in 1908 he publishes his own proof based on the chain theory from Dedekind's paper Was sind und was sollen die Zahlen?
• 1895 Cantor states the theorem in his first paper on set theory and transfinite numbers. He obtains it as an easy consequence of the linear order of cardinal numbers. However, he could not prove the latter theorem, which is shown in 1915 to be equivalent to the axiom of choice by Friedrich Moritz Hartogs.
• 1896 Schröder announces a proof (as a corollary of a theorem by Jevons).
• 1897 Bernstein, a 19-year-old student in Cantor's Seminar, presents his proof.
• 1897 Almost simultaneously, but independently, Schröder finds a proof.
• 1897 After a visit by Bernstein, Dedekind independently proves the theorem a second time.
• 1898 Bernstein's proof (not relying on the axiom of choice) is published by Émile Borel in his book on functions. (Communicated by Cantor at the 1897 International Congress of Mathematicians in Zürich.) In the same year, the proof also appears in Bernstein's dissertation.
• 1898 Schröder publishes his proof which, however, is shown to be faulty by Alwin Reinhold Korselt in 1902 (just before Schröder's death), (confirmed by Schröder), but Korselt's paper is published only in 1911.

Both proofs of Dedekind are based on his famous 1888 memoir Was sind und was sollen die Zahlen? and derive it as a corollary of a proposition equivalent to statement C in Cantor's paper, which reads A ⊆ B ⊆ C and |A| = |C| implies |A| = |B| = |C|. Cantor observed this property as early as 1882/83 during his studies in set theory and transfinite numbers and was therefore (implicitly) relying on the axiom of choice.

Prerequisites

The 1895 proof by Cantor relied, in effect, on the axiom of choice by inferring the result as a corollary of the well-ordering theorem. However, König's proof given above shows that the result can also be proved without using the axiom of choice.

On the other hand, König's proof uses the principle of excluded middle to draw a conclusion through case analysis. As such, the above proof is not a constructive one. In fact, in a constructive set theory such as intuitionistic set theory ${\displaystyle {\mathsf {IZF}}}$, which adopts the full axiom of separation but dispenses with the principle of excluded middle, assuming the Schröder–Bernstein theorem implies the latter. In turn, there is no proof of König's conclusion in this or weaker constructive theories. Therefore, intuitionists do not accept the statement of the Schröder–Bernstein theorem.

There is also a proof which uses Tarski's fixed point theorem.

See also

• Myhill isomorphism theorem
• Netto's theorem, according to which the bijections constructed by the Schröder–Bernstein theorem between spaces of different dimensions cannot be continuous
• Schröder–Bernstein theorem for measurable spaces
• Schröder–Bernstein theorems for operator algebras
• Schröder–Bernstein property

Notes

1. J. König (1906). "Sur la théorie des ensembles". Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. 143: 110–112.
2. ^ Felix Hausdorff (2002), Egbert Brieskorn; Srishti D. Chatterji; et al. (eds.), Grundzüge der Mengenlehre (1. ed.), Berlin/Heidelberg: Springer, p. 587, ISBN 978-3-540-42224-2 – Original edition (1914)
3. ^ Georg Cantor (1887), "Mitteilungen zur Lehre vom Transfiniten", Zeitschrift für Philosophie und philosophische Kritik, 91: 81–125
   Reprinted in: Georg Cantor (1932), Adolf Fraenkel (Lebenslauf); Ernst Zermelo (eds.), Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, Berlin: Springer, pp. 378–439 Here: p.413 bottom
4. Richard Dedekind (1932), Robert Fricke; Emmy Noether; Øystein Ore (eds.), Gesammelte mathematische Werke, vol. 3, Braunschweig: Friedr. Vieweg & Sohn, pp. 447–449 (Ch.62)
5. Ernst Zermelo (1908), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Untersuchungen über die Grundlagen der Mengenlehre I", Mathematische Annalen, 65 (2): 261–281, here: p.271–272, doi:10.1007/bf01449999, ISSN 0025-5831, S2CID 120085563
6. Richard Dedekind (1888), Was sind und was sollen die Zahlen? (2., unchanged (1893) ed.), Braunschweig: Friedr. Vieweg & Sohn
7. ^ Georg Cantor (1932), Adolf Fraenkel (Lebenslauf); Ernst Zermelo (eds.), Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, Berlin: Springer, pp. 285 ("Satz B")
8. ^ Georg Cantor (1895). "Beiträge zur Begründung der transfiniten Mengenlehre (1)". Mathematische Annalen. 46 (4): 481–512 (Theorem see "Satz B", p.484). doi:10.1007/bf02124929. S2CID 177801164.
9. ^ (Georg Cantor (1897). "Beiträge zur Begründung der transfiniten Mengenlehre (2)". Mathematische Annalen. 49 (2): 207–246. doi:10.1007/bf01444205. S2CID 121665994.)
10. Friedrich M. Hartogs (1915), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Über das Problem der Wohlordnung", Mathematische Annalen, 76 (4): 438–443, doi:10.1007/bf01458215, ISSN 0025-5831, S2CID 121598654
11. Ernst Schröder (1896). "Über G. Cantorsche Sätze". Jahresbericht der Deutschen Mathematiker-Vereinigung. 5: 81–82.
12. ^ Oliver Deiser (2010), Einführung in die Mengenlehre – Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo, Springer-Lehrbuch (3rd, corrected ed.), Berlin/Heidelberg: Springer, pp. 71, 501, doi:10.1007/978-3-642-01445-1, ISBN 978-3-642-01444-4
13. ^ Patrick Suppes (1972), Axiomatic Set Theory (1. ed.), New York: Dover Publications, pp. 95 f, ISBN 978-0-486-61630-8
14. Émile Borel (1898), Leçons sur la théorie des fonctions, Paris: Gauthier-Villars et fils, pp. 103 ff
15. Felix Bernstein (1901), Untersuchungen aus der Mengenlehre, Halle a. S.: Buchdruckerei des Waisenhauses
    Reprinted in: Felix Bernstein (1905), Felix Klein; Walther von Dyck; David Hilbert (eds.), "Untersuchungen aus der Mengenlehre", Mathematische Annalen, 61 (1): 117–155, (Theorem see "Satz 1" on p.121), doi:10.1007/bf01457734, ISSN 0025-5831, S2CID 119658724
16. Ernst Schröder (1898), Kaiserliche Leopoldino-Carolinische Deutsche Akademie der Naturforscher (ed.), "Ueber zwei Definitionen der Endlichkeit und G. Cantor'sche Sätze", Nova Acta, 71 (6): 303–376 (proof: p.336–344)
17. Alwin R. Korselt (1911), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Über einen Beweis des Äquivalenzsatzes", Mathematische Annalen, 70 (2): 294–296, doi:10.1007/bf01461161, ISSN 0025-5831, S2CID 119757900
18. Korselt (1911), p.295
19. Pradic, Cécilia; Brown, Chad E. (2019). "Cantor-Bernstein implies Excluded Middle". arXiv:1904.09193 .
20. Ettore Carruccio (2006). Mathematics and Logic in History and in Contemporary Thought. Transaction Publishers. p. 354. ISBN 978-0-202-30850-0.
21. Roland Uhl. "Tarski's Fixed Point Theorem". MathWorld. Example 3.

References

• Martin Aigner & Gunter M. Ziegler (1998) Proofs from THE BOOK, § 3 Analysis: Sets and functions, Springer books MR1723092, fifth edition 2014 MR3288091, sixth edition 2018 MR3823190
• Hinkis, Arie (2013), Proofs of the Cantor-Bernstein theorem. A mathematical excursion, Science Networks. Historical Studies, vol. 45, Heidelberg: Birkhäuser/Springer, doi:10.1007/978-3-0348-0224-6, ISBN 978-3-0348-0223-9, MR 3026479
• Searcóid, Míchaél Ó (2013). "On the history and mathematics of the equivalence theorem". Mathematical Proceedings of the Royal Irish Academy. 113A (2): 151–68. doi:10.1353/mpr.2013.0006. JSTOR 42912521. S2CID 245841055.

External links

• Weisstein, Eric W. "Schröder-Bernstein Theorem". MathWorld.
• Cantor-Schroeder-Bernstein theorem at the nLab
• Cantor-Bernstein’s Theorem in a Semiring by Marcel Crabbé.
• This article incorporates material from the Citizendium article "Schröder-Bernstein_theorem", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.

v t e Set theory
Overview	Set (mathematics)
Axioms	Adjunction Choice countable dependent global Constructibility (V=L) Determinacy projective Extensionality Infinity Limitation of size Pairing Power set Regularity Union Martin's axiom Axiom schema replacement specification
Operations	Cartesian product Complement (i.e. set difference) De Morgan's laws Disjoint union Identities Intersection Power set Symmetric difference Union
Concepts Methods	Almost Cardinality Cardinal number (large) Class Constructible universe Continuum hypothesis Diagonal argument Element ordered pair tuple Family Forcing One-to-one correspondence Ordinal number Set-builder notation Transfinite induction Venn diagram
Set types	Amorphous Countable Empty Finite (hereditarily) Filter base subbase Ultrafilter Fuzzy Infinite (Dedekind-infinite) Recursive Singleton Subset · Superset Transitive Uncountable Universal
Theories	Alternative Axiomatic Naive Cantor's theorem Zermelo General Principia Mathematica New Foundations Zermelo–Fraenkel von Neumann–Bernays–Gödel Morse–Kelley Kripke–Platek Tarski–Grothendieck
Paradoxes Problems	Russell's paradox Suslin's problem Burali-Forti paradox
Set theorists	Paul Bernays Georg Cantor Paul Cohen Richard Dedekind Abraham Fraenkel Kurt Gödel Thomas Jech John von Neumann Willard Quine Bertrand Russell Thoralf Skolem Ernst Zermelo

v t e Mathematical logic
General	Axiom list Cardinality First-order logic Formal proof Formal semantics Foundations of mathematics Information theory Lemma Logical consequence Model Theorem Theory Type theory
Theorems (list)  and paradoxes	Gödel's completeness and incompleteness theorems Tarski's undefinability Banach–Tarski paradox Cantor's theorem, paradox and diagonal argument Compactness Halting problem Lindström's Löwenheim–Skolem Russell's paradox
Logics	Traditional Classical logic Logical truth Tautology Proposition Inference Logical equivalence Consistency Equiconsistency Argument Soundness Validity Syllogism Square of opposition Venn diagram Propositional Boolean algebra Boolean functions Logical connectives Propositional calculus Propositional formula Truth tables Many-valued logic 3 finite ∞ Predicate First-order list Second-order Monadic Higher-order Fixed-point Free Quantifiers Predicate Monadic predicate calculus
Set theory	Set hereditary Class (Ur-)Element Ordinal number Extensionality Forcing Relation equivalence partition Set operations: intersection union complement Cartesian product power set identities Types of sets Countable Uncountable Empty Inhabited Singleton Finite Infinite Transitive Ultrafilter Recursive Fuzzy Universal Universe constructible Grothendieck Von Neumann Maps and cardinality Function/Map domain codomain image In/Sur/Bi-jection Schröder–Bernstein theorem Isomorphism Gödel numbering Enumeration Large cardinal inaccessible Aleph number Operation binary Set theories Zermelo–Fraenkel axiom of choice continuum hypothesis General Kripke–Platek Morse–Kelley Naive New Foundations Tarski–Grothendieck Von Neumann–Bernays–Gödel Ackermann Constructive
Formal systems (list), language and syntax	Alphabet Arity Automata Axiom schema Expression ground Extension by definition conservative Relation Formation rule Grammar Formula atomic closed ground open Free/bound variable Language Metalanguage Logical connective ¬ ∨ ∧ → ↔ = Predicate functional variable propositional variable Proof Quantifier ∃ ! ∀ rank Sentence atomic spectrum Signature String Substitution Symbol function logical/constant non-logical variable Term Theory list Example axiomatic systems (list) of arithmetic: Peano second-order elementary function primitive recursive Robinson Skolem of the real numbers Tarski's axiomatization of Boolean algebras canonical minimal axioms of geometry: Euclidean: Elements Hilbert's Tarski's non-Euclidean Principia Mathematica
Proof theory	Formal proof Natural deduction Logical consequence Rule of inference Sequent calculus Theorem Systems axiomatic deductive Hilbert list Complete theory Independence (from ZFC) Proof of impossibility Ordinal analysis Reverse mathematics Self-verifying theories
Model theory	Interpretation function of models Model equivalence finite saturated spectrum submodel Non-standard model of arithmetic Diagram elementary Categorical theory Model complete theory Satisfiability Semantics of logic Strength Theories of truth semantic Tarski's Kripke's T-schema Transfer principle Truth predicate Truth value Type Ultraproduct Validity
Computability theory	Church encoding Church–Turing thesis Computably enumerable Computable function Computable set Decision problem decidable undecidable P NP P versus NP problem Kolmogorov complexity Lambda calculus Primitive recursive function Recursion Recursive set Turing machine Type theory
Related	Abstract logic Algebraic logic Automated theorem proving Category theory Concrete/Abstract category Category of sets History of logic History of mathematical logic timeline Logicism Mathematical object Philosophy of mathematics Supertask
Mathematics portal

• Theorems in the foundations of mathematics
• Cardinal numbers