Misplaced Pages

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Cantor distribution" – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message)

Cantor

Cumulative distribution function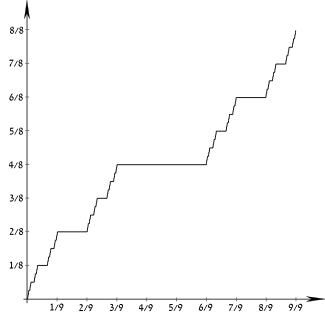
Parameters	none
Support	Cantor set, a subset of
PMF	none
CDF	Cantor function
Mean	1/2
Median	anywhere in
Mode	n/a
Variance	1/8
Skewness	0
Excess kurtosis	−8/5
MGF	${\displaystyle e^{t/2}\prod _{k=1}^{\infty }\cosh \left({\frac {t}{3^{k}}}\right)}$
CF	${\displaystyle e^{it/2}\prod _{k=1}^{\infty }\cos \left({\frac {t}{3^{k}}}\right)}$

The Cantor distribution is the probability distribution whose cumulative distribution function is the Cantor function.

This distribution has neither a probability density function nor a probability mass function, since although its cumulative distribution function is a continuous function, the distribution is not absolutely continuous with respect to Lebesgue measure, nor does it have any point-masses. It is thus neither a discrete nor an absolutely continuous probability distribution, nor is it a mixture of these. Rather it is an example of a singular distribution.

Its cumulative distribution function is continuous everywhere but horizontal almost everywhere, so is sometimes referred to as the Devil's staircase, although that term has a more general meaning.

Characterization

The support of the Cantor distribution is the Cantor set, itself the intersection of the (countably infinitely many) sets:

${\displaystyle {\begin{aligned}C_{0}={}&\\C_{1}={}&\cup \\C_{2}={}&\cup \cup \cup \\C_{3}={}&\cup \cup \cup \cup \\{}&\cup \cup \cup \\C_{4}={}&\cup \cup \cup \cup \cup \cup \\&\cup \cup \cup \cup \cup \\&\cup \cup \cup \cup \\C_{5}={}&\cdots \end{aligned}}}$

The Cantor distribution is the unique probability distribution for which for any C_t (t ∈ { 0, 1, 2, 3, ... }), the probability of a particular interval in C_t containing the Cantor-distributed random variable is identically 2 on each one of the 2 intervals.

Moments

It is easy to see by symmetry and being bounded that for a random variable X having this distribution, its expected value E(X) = 1/2, and that all odd central moments of X are 0.

The law of total variance can be used to find the variance var(X), as follows. For the above set C₁, let Y = 0 if X ∈ , and 1 if X ∈ . Then:

${\displaystyle {\begin{aligned}\operatorname {var} (X)&=\operatorname {E} (\operatorname {var} (X\mid Y))+\operatorname {var} (\operatorname {E} (X\mid Y))\\&={\frac {1}{9}}\operatorname {var} (X)+\operatorname {var} \left\{{\begin{matrix}1/6&{\mbox{with probability}}\ 1/2\\5/6&{\mbox{with probability}}\ 1/2\end{matrix}}\right\}\\&={\frac {1}{9}}\operatorname {var} (X)+{\frac {1}{9}}\end{aligned}}}$

From this we get:

${\displaystyle \operatorname {var} (X)={\frac {1}{8}}.}$

A closed-form expression for any even central moment can be found by first obtaining the even cumulants

${\displaystyle \kappa _{2n}={\frac {2^{2n-1}(2^{2n}-1)B_{2n}}{n\,(3^{2n}-1)}},\,\!}$

where B_2n is the 2nth Bernoulli number, and then expressing the moments as functions of the cumulants.

References

1. Morrison, Kent (1998-07-23). "Random Walks with Decreasing Steps" (PDF). Department of Mathematics, California Polytechnic State University. Archived from the original (PDF) on 2015-12-02. Retrieved 2007-02-16.

Further reading

• Hewitt, E.; Stromberg, K. (1965). Real and Abstract Analysis. Berlin-Heidelberg-New York: Springer-Verlag. This, as with other standard texts, has the Cantor function and its one sided derivates.
• Hu, Tian-You; Lau, Ka Sing (2002). "Fourier Asymptotics of Cantor Type Measures at Infinity". Proc. AMS. Vol. 130, no. 9. pp. 2711–2717. This is more modern than the other texts in this reference list.
• Knill, O. (2006). Probability Theory & Stochastic Processes. India: Overseas Press.
• Mattilla, P. (1995). Geometry of Sets in Euclidean Spaces. San Francisco: Cambridge University Press. This has more advanced material on fractals.

• Continuous distributions
• Georg Cantor