Misplaced Pages

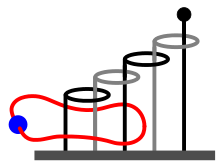
Baguenaudier (pronounced [baɡnodje]; French for "time-waster"), also known as the Chinese rings, Cardan's suspension, Cardano's rings, Devil's needle or five pillars puzzle, is a disentanglement puzzle featuring a loop which must be disentangled from a sequence of rings on interlinked pillars. The loop can be either string or a rigid structure.

It is thought to have been invented originally in China. The origins are obscure. The American ethnographer Stewart Culin related a tradition attributing the puzzle's invention to the 2nd/3rd century Chinese general Zhuge Liang. It was used by French peasants as a locking mechanism.

Variations of this include the Devil's staircase, Devil's Halo and the impossible staircase. Another similar puzzle is the Giant's causeway which uses a separate pillar with an embedded ring.

Mathematical solution

The 19th-century French mathematician Édouard Lucas, the inventor of the Tower of Hanoi puzzle, was known to have come up with an elegant solution which used binary and Gray codes, in the same way that his puzzle can be solved. The minimum number of moves to solve an n-ringed problem has been found to be

${\displaystyle a(n)={\begin{cases}{\dfrac {2^{n+1}-2}{3}}&{\text{when }}n{\text{ is even,}}\\{\dfrac {2^{n+1}-1}{3}}&{\text{when }}n{\text{ is odd.}}\end{cases}}}$

For other formulae, see OEIS sequence A000975.

See also

• ABACABA pattern
• Disentanglement puzzle
• Towers of Hanoi

References

Part of a series on
Puzzles
Types Guessing Riddle Situation Logic Dissection Induction Logic grid Self-reference Mechanical Combination Construction Disentanglement Lock Go problems Folding Stick Tiling Tour Sliding Chess Maze (Logic maze) Word and Number Crossword Sudoku Puzzle video games Mazes Metapuzzles
Topics Brain teaser Dilemma Joke Optical illusion Packing problems Paradox Problem solving Puzzlehunt Syllogism Tale
Lists Impossible puzzles Maze video games Nikoli puzzle types Puzzle video games Puzzle topics
v t e

1. ^ Weisstein, Eric W. "Baguenaudier". MathWorld.
2. ^ David Darling. "Chinese rings". Encyclopedia of Science.
3. Hinz, Andreas M.; Klavžar, Sandi; Milutinović, Uroš; Petr, Ciril (2015). The Tower of Hanoi – Myths and Maths. Birkhäuser. p. 4. ISBN 978-3034807692.
4. "The Devil's Halo". The Puzzle Museum. 2017.

• Chinese ancient games
• Chinese inventions
• Educational toys
• Mechanical puzzles