| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Carnot heat engine" – news · newspapers · books · scholar · JSTOR (October 2018) (Learn how and when to remove this message) |

A Carnot heat engine is a theoretical heat engine that operates on the Carnot cycle. The basic model for this engine was developed by Nicolas Léonard Sadi Carnot in 1824. The Carnot engine model was graphically expanded by Benoît Paul Émile Clapeyron in 1834 and mathematically explored by Rudolf Clausius in 1857, work that led to the fundamental thermodynamic concept of entropy. The Carnot engine is the most efficient heat engine which is theoretically possible. The efficiency depends only upon the absolute temperatures of the hot and cold heat reservoirs between which it operates.
A heat engine acts by transferring energy from a warm region to a cool region of space and, in the process, converting some of that energy to mechanical work. The cycle may also be reversed. The system may be worked upon by an external force, and in the process, it can transfer thermal energy from a cooler system to a warmer one, thereby acting as a refrigerator or heat pump rather than a heat engine.
Every thermodynamic system exists in a particular state. A thermodynamic cycle occurs when a system is taken through a series of different states, and finally returned to its initial state. In the process of going through this cycle, the system may perform work on its surroundings, thereby acting as a heat engine.
The Carnot engine is a theoretical construct, useful for exploring the efficiency limits of other heat engines. An actual Carnot engine, however, would be completely impractical to build.
Carnot's diagram
In the adjacent diagram, from Carnot's 1824 work, Reflections on the Motive Power of Fire, there are "two bodies A and B, kept each at a constant temperature, that of A being higher than that of B. These two bodies to which we can give, or from which we can remove the heat without causing their temperatures to vary, exercise the functions of two unlimited reservoirs of caloric. We will call the first the furnace and the second the refrigerator." Carnot then explains how we can obtain motive power, i.e., "work", by carrying a certain quantity of heat from body A to body B. It also acts as a cooler and hence can also act as a refrigerator.
Modern diagram

The previous image shows the original piston-and-cylinder diagram used by Carnot in discussing his ideal engine. The figure at right shows a block diagram of a generic heat engine, such as the Carnot engine. In the diagram, the "working body" (system), a term introduced by Clausius in 1850, can be any fluid or vapor body through which heat Q can be introduced or transmitted to produce work. Carnot had postulated that the fluid body could be any substance capable of expansion, such as vapor of water, vapor of alcohol, vapor of mercury, a permanent gas, air, etc. Although in those early years, engines came in a number of configurations, typically QH was supplied by a boiler, wherein water was boiled over a furnace; QC was typically removed by a stream of cold flowing water in the form of a condenser located on a separate part of the engine. The output work, W, is transmitted by the movement of the piston as it is used to turn a crank-arm, which in turn was typically used to power a pulley so as to lift water out of flooded salt mines. Carnot defined work as "weight lifted through a height".
Carnot cycle
Main article: Carnot cycle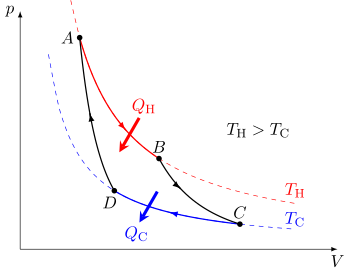
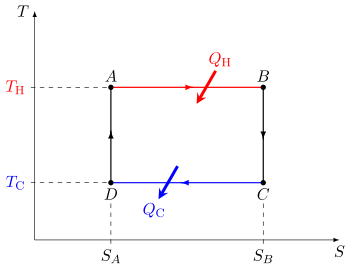
The Carnot cycle when acting as a heat engine consists of the following steps:
- Reversible isothermal expansion of the gas at the "hot" temperature, TH (isothermal heat addition or absorption). During this step (A to B) the gas is allowed to expand and it does work on the surroundings. The temperature of the gas (the system) does not change during the process, and thus the expansion is isothermic. The gas expansion is propelled by absorption of heat energy QH and of entropy ΔSH = QH / TH from the high temperature reservoir.
- Isentropic (reversible adiabatic) expansion of the gas (isentropic work output). For this step (B to C) the piston and cylinder are assumed to be thermally insulated, thus they neither gain nor lose heat. The gas continues to expand, doing work on the surroundings, and losing an equivalent amount of internal energy. The gas expansion causes it to cool to the "cold" temperature, TC. The entropy remains unchanged.
- Reversible isothermal compression of the gas at the "cold" temperature, TC (isothermal heat rejection) (C to D). Now the gas is exposed to the cold temperature reservoir while the surroundings do work on the gas by compressing it (such as through the return compression of a piston), while causing an amount of waste heat QC < 0 (with the standard sign convention for heat) and of entropy ΔSC = QC/TC < 0 to flow out of the gas to the low temperature reservoir. (In magnitude, this is the same amount of entropy absorbed in step 1. The entropy decreases in isothermal compression since the multiplicity of the system decreases with the volume.) In terms of magnitude, the recompression work performed by the surroundings in this step is less than the work performed on the surroundings in step 1 because it occurs at a lower pressure due to the lower temperature (i.e. the resistance to compression is lower under step 3 than the force of expansion under step 1). We can refer to the first law of thermodynamics to explain this behavior: ΔU= W+Q .
- Isentropic compression of the gas (isentropic work input) (D to A). Once again the piston and cylinder are assumed to be thermally insulated and the cold temperature reservoir is removed. During this step, the surroundings continue to do work to further compress the gas and both the temperature and pressure rise now that the heat sink has been removed. This additional work increases the internal energy of the gas, compressing it and causing the temperature to rise to TH. The entropy remains unchanged. At this point the gas is in the same state as at the start of step 1.
Carnot's theorem
Main article: Carnot's theorem (thermodynamics)
Carnot's theorem is a formal statement of this fact: No engine operating between two heat reservoirs can be more efficient than a Carnot engine operating between the same reservoirs.
Explanation
This maximum efficiency ηI is defined as above:
- W is the work done by the system (energy exiting the system as work),
- QH is the heat put into the system (heat energy entering the system),
- TC is the absolute temperature of the cold reservoir, and
- TH is the absolute temperature of the hot reservoir.
A corollary to Carnot's theorem states that: All reversible engines operating between the same heat reservoirs are equally efficient.
It is easily shown that the efficiency η is maximum when the entire cyclic process is a reversible process. This means the total entropy of system and surroundings (the entropies of the hot furnace, the "working fluid" of the heat engine, and the cold sink) remains constant when the "working fluid" completes one cycle and returns to its original state. (In the general and more realistic case of an irreversible process, the total entropy of this combined system would increase.)
Since the "working fluid" comes back to the same state after one cycle, and entropy of the system is a state function, the change in entropy of the "working fluid" system is 0. Thus, it implies that the total entropy change of the furnace and sink is zero, for the process to be reversible and the efficiency of the engine to be maximum. This derivation is carried out in the next section.
The coefficient of performance (COP) of the heat engine is the reciprocal of its efficiency.
Efficiency of real heat engines
For a real heat engine, the total thermodynamic process is generally irreversible. The working fluid is brought back to its initial state after one cycle, and thus the change of entropy of the fluid system is 0, but the sum of the entropy changes in the hot and cold reservoir in this one cyclical process is greater than 0.
The internal energy of the fluid is also a state variable, so its total change in one cycle is 0. So the total work done by the system W is equal to the net heat put into the system, the sum of > 0 taken up and the waste heat < 0 given off:
| 2 |
For real engines, stages 1 and 3 of the Carnot cycle, in which heat is absorbed by the "working fluid" from the hot reservoir, and released by it to the cold reservoir, respectively, no longer remain ideally reversible, and there is a temperature differential between the temperature of the reservoir and the temperature of the fluid while heat exchange takes place.
During heat transfer from the hot reservoir at to the fluid, the fluid would have a slightly lower temperature than , and the process for the fluid may not necessarily remain isothermal. Let be the total entropy change of the fluid in the process of intake of heat.
| 3 |
where the temperature of the fluid T is always slightly lesser than , in this process.
So, one would get:
| 4 |
Similarly, at the time of heat injection from the fluid to the cold reservoir one would have, for the magnitude of total entropy change < 0 of the fluid in the process of expelling heat:
| 5 |
where, during this process of transfer of heat to the cold reservoir, the temperature of the fluid T is always slightly greater than .
We have only considered the magnitude of the entropy change here. Since the total change of entropy of the fluid system for the cyclic process is 0, we must have
| 6 |
The previous three equations, namely (3), (4), (5), substituted into (6) to give:
| 7 |
| This section may be very hard to understand. Please help clarify it. (January 2024) |
For + = 0
= -
=
it is at least (Qh/Th) ≤ (-Qc/Tc)
Equations (2) and (7) combine to give
| 8 |
To derive this step needs two adiabatic processes involved to show an isentropic process property for the ratio of the changing volumes of two isothermal processes are equal.
Most importantly, since the two adiabatic processes are volume works without heat lost, and since the ratio of volume changes for this two processes are the same, so the works for these two adiabatic processes are the same with opposite direction to each other, namely, one direction is work done by the system and the other is work done on the system; therefore, heat efficiency only concerns the amount of work done by the heat absorbed comparing to the amount of heat absorbed by the system.
Therefore, (W/Qh) = (Qh - Qc) / Qh
= 1 - (Qc/Qh)
= 1 - (Tc/Th)
And, from (7)
(Qh/Th) ≤ (-Qc/Tc) here Qc it is less than 0 (release heat)
(Tc/Th) ≤ (-Qc/Qh)
-(Tc/Th) ≥ (Qc/Qh)
1+ ≥ 1+(Qc/Qh)
1 - (Tc/Th) ≥ (Qh + Qc)/Qh here Qc<0,
1 - (Tc/Th) ≥ (Qh - Qc)/Qh
1 - (Tc/Th) ≥ W/Qh
Hence,
| 9 |
where is the efficiency of the real engine, and is the efficiency of the Carnot engine working between the same two reservoirs at the temperatures and . For the Carnot engine, the entire process is 'reversible', and Equation (7) is an equality. Hence, the efficiency of the real engine is always less than the ideal Carnot engine.
Equation (7) signifies that the total entropy of system and surroundings (the fluid and the two reservoirs) increases for the real engine, because (in a surroundings-based analysis) the entropy gain of the cold reservoir as flows into it at the fixed temperature , is greater than the entropy loss of the hot reservoir as leaves it at its fixed temperature . The inequality in Equation (7) is essentially the statement of the Clausius theorem.
According to the second theorem, "The efficiency of the Carnot engine is independent of the nature of the working substance".
The Carnot engine and Rudolf Diesel
In 1892 Rudolf Diesel patented an internal combustion engine inspired by the Carnot engine. Diesel knew a Carnot engine is an ideal that cannot be built, but he thought he had invented a working approximation. His principle was unsound, but in his struggle to implement it he developed a practical Diesel engine.
The conceptual problem was how to achieve isothermal expansion in an internal combustion engine, since burning fuel at the highest temperature of the cycle would only raise the temperature further. Diesel's patented solution was: having achieved the highest temperature just by compressing the air, to add a small amount of fuel at a controlled rate, such that heating caused by burning the fuel would be counteracted by cooling caused by air expansion as the piston moved. Hence all the heat from the fuel would be transformed into work during the isothermal expansion, as required by Carnot's theorem.
For the idea to work a small mass of fuel would have to be burnt in a huge mass of air. Diesel first proposed a working engine that would compress air to 250 atmospheres at 800 °C (1,450 °F), then cycle to one atmosphere at 20 °C (50 °F). However, this was well beyond the technological capabilities of the day, since it implied a compression ratio of 60:1. Such an engine, if it could have been built, would have had an efficiency of 73%. (In contrast, the best steam engines of his day achieved 7%.)
Accordingly, Diesel sought to compromise. He calculated that, were he to reduce the peak pressure to a less ambitious 90 atmospheres, he would sacrifice only 5% of the thermal efficiency. Seeking financial support, he published the "Theory and Construction of a Rational Heat Engine to Take the Place of the Steam Engine and All Presently Known Combustion Engines" (1893). Endorsed by scientific opinion, including Lord Kelvin, he won the backing of Krupp and Maschinenfabrik Augsburg. He clung to the Carnot cycle as a symbol. But years of practical work failed to achieve an isothermal combustion engine, nor could have done, since it requires such an enormous quantity of air that it cannot develop enough power to compress it. Furthermore, controlled fuel injection turned out to be no easy matter.
Even so, the Diesel engine slowly evolved over 25 years to become a practical high-compression air engine, its fuel injected near the end of the compression stroke and ignited by the heat of compression, capable by 1969 of 40% efficiency.
As a macroscopic construct
The Carnot heat engine is, ultimately, a theoretical construct based on an idealized thermodynamic system. On a practical human-scale level the Carnot cycle has proven a valuable model, as in advancing the development of the diesel engine. However, on a macroscopic scale limitations placed by the model's assumptions prove it impractical, and, ultimately, incapable of doing any work. As such, per Carnot's theorem, the Carnot engine may be thought as the theoretical limit of macroscopic scale heat engines rather than any practical device that could ever be built.
For example, for the isothermal expansion part of the Carnot cycle, the following infinitesimal conditions must be satisfied simultaneously at every step in the expansion:
- The hot reservoir temperature TH is infinitesimally higher than the system gas temperature T so heat flow (energy transfer) from the hot reservoir to the gas is made without increasing T (via infinitesimal work on the surroundings by the gas as another energy transfer); if TH is significantly higher than T, then T may be not uniform through the gas so the system would deviate from thermal equilibrium as well as not being a reversible process (i.e. not a Carnot cycle) or T might increase noticeably so it would not be an isothermal process.
- The force externally applied on the piston (opposite to the internal force on the piston by the gas) needs to be infinitesimally reduced externally. Without this assistance, it would not be possible to follow a gas PV (Pressure-Volume) curve downward at a constant T since following this curve means that the gas-to-piston force decreases (P decreases) as the volume expands (the piston moves outward). If this assistance is so strong that the volume expansion is significant, the system may deviate from thermal equilibrium, and the process fail to be reversible (and thus not a Carnot cycle).
Such "infinitesimal" requirements as these (and others) cause the Carnot cycle to take an infinite amount of time, rendering the production of work impossible.
Other practical requirements that make the Carnot cycle impractical to realize include fine control of the gas, and perfect thermal contact with the surroundings (including high and low temperature reservoirs).
Notes
- Figure 1 in Carnot (1824, p. 17) and Carnot (1890, p. 63). In the diagram, the diameter of the vessel is large enough to bridge the space between the two bodies, but in the model, the vessel is never in contact with both bodies simultaneously. Also, the diagram shows an unlabeled axial rod attached to the outside of the piston.
- In French, Carnot uses machine à feu, which Thurston translates as heat-engine or steam-engine. In a footnote, Carnot distinguishes the steam-engine (machine à vapeur) from the heat-engine in general. (Carnot, 1824, p. 5 and Carnot, 1890, p. 43)
- "The Carnot Efficiency | EGEE 102: Energy Conservation and Environmental Protection". www.e-education.psu.edu. Retrieved 2022-01-24.
- "Sometimes translated as Reflections on the Motive Power of Heat".
- English translation by Thurston (Carnot, 1890, p. 51-52).
- Planck, M. (1945). Treatise on Thermodynamics. Dover Publications. p. 90.
§90, eqs.(39) & (40)
- Fermi, E. (1956). Thermodynamics. Dover Publications (still in print). p. 47.
below eq.(63)
- Bryant, Lynwood (August 1969). "Rudolf Diesel and His Rational Engine". Scientific American. 221 (2): 108–117. Bibcode:1969SciAm.221b.108B. doi:10.1038/scientificamerican0869-108. JSTOR 24926442.
- ^ Liu, Hang; Meng, Xin-He (2017-08-18). "Effects of dark energy on the efficiency of charged AdS black holes as heat engines". The European Physical Journal C. 77 (8): 556. arXiv:1704.04363. doi:10.1140/epjc/s10052-017-5134-9. ISSN 1434-6052.
...since the Carnot heat engine, setting an upper bound on the efficiency of a heat engine is an ideal, reversible engine of which a single cycle must be performed in infinite time which is impractical and so the Carnot engine has zero power.
- Benenti, Giuliano; Casati, Giulio; Wang, Jiao (2020). "Power, efficiency, and fluctuations in steady-state heat engines" (PDF). Physical Review E. 102 (4).
However, fluctuations make impractical such engines.
- D, Bob (2020-01-15). "In the isothermal expansion phase of a Carnot cycle, why does the gas expand?". StackExchange. Retrieved 2022-01-02.
External links
Episode 46. Engine of Nature: The Carnot engine, part one, beginning with simple steam engines. The Mechanical Universe. Caltech – via YouTube.
References
- Bryant, Lynwood (August 1969). "Rudolf Diesel and His Rational Engine". Scientific American. 221 (2): 108–117. Bibcode:1969SciAm.221b.108B. doi:10.1038/scientificamerican0869-108. JSTOR 24926442.
- Carnot, Sadi (1824). Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance (in French). Paris: Bachelier. (First Edition 1824) and (Reissued Edition of 1878)
- Carnot, Sadi (1890). Thurston, Robert Henry (ed.). Reflections on the Motive Power of Heat and on Machines Fitted to Develop That Power. New York: J. Wiley & Sons. (full text of 1897 ed.) (Archived HTML version)
| Heat engines | |
|---|---|
| Thermodynamic cycle |

 > 0 taken up and the waste heat
> 0 taken up and the waste heat  < 0 given off:
< 0 given off:

 to the fluid, the fluid would have a slightly lower temperature than
to the fluid, the fluid would have a slightly lower temperature than  be the total entropy change of the fluid in the process of intake of heat.
be the total entropy change of the fluid in the process of intake of heat.


 < 0 of the fluid in the process of expelling heat:
< 0 of the fluid in the process of expelling heat:

 .
.




 is the efficiency of the real engine, and
is the efficiency of the real engine, and  is the efficiency of the Carnot engine working between the same two reservoirs at the temperatures
is the efficiency of the Carnot engine working between the same two reservoirs at the temperatures