Misplaced Pages

Part of a series on
Network science
Theory
Graph Complex network Contagion Small-world Scale-free Community structure Percolation Evolution Controllability Graph drawing Social capital Link analysis Optimization Reciprocity Closure Homophily Transitivity Preferential attachment Balance theory Network effect Social influence
Network types
Informational (computing) Telecommunication Transport Social Scientific collaboration Biological Artificial neural Interdependent Semantic Spatial Dependency Flow on-Chip
Graphs
Features Clique Component Cut Cycle Data structure Edge Loop Neighborhood Path Vertex Adjacency list / matrix Incidence list / matrix Types Bipartite Complete Directed Hyper Labeled Multi Random Weighted
Metrics Algorithms
Centrality Degree Motif Clustering Degree distribution Assortativity Distance Modularity Efficiency
Models
Topology Random graph Erdős–Rényi Barabási–Albert Bianconi–Barabási Fitness model Watts–Strogatz Exponential random (ERGM) Random geometric (RGG) Hyperbolic (HGN) Hierarchical Stochastic block Blockmodeling Maximum entropy Soft configuration LFR Benchmark Dynamics Boolean network agent based Epidemic/SIR
Lists Categories
Topics Software Network scientists Category:Network theory Category:Graph theory
v t e

In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.

Definition and characterization of centrality indices

Centrality indices are answers to the question "What characterizes an important vertex?" The answer is given in terms of a real-valued function on the vertices of a graph, where the values produced are expected to provide a ranking which identifies the most important nodes.

The word "importance" has a wide number of meanings, leading to many different definitions of centrality. Two categorization schemes have been proposed. "Importance" can be conceived in relation to a type of flow or transfer across the network. This allows centralities to be classified by the type of flow they consider important. "Importance" can alternatively be conceived as involvement in the cohesiveness of the network. This allows centralities to be classified based on how they measure cohesiveness. Both of these approaches divide centralities in distinct categories. A further conclusion is that a centrality which is appropriate for one category will often "get it wrong" when applied to a different category.

Many, though not all, centrality measures effectively count the number of paths (also called walks) of some type going through a given vertex; the measures differ in how the relevant walks are defined and counted. Restricting consideration to this group allows for taxonomy which places many centralities on a spectrum from those concerned with walks of length one (degree centrality) to infinite walks (eigenvector centrality). Other centrality measures, such as betweenness centrality focus not just on overall connectedness but occupying positions that are pivotal to the network's connectivity.

Characterization by network flows

A network can be considered a description of the paths along which something flows. This allows a characterization based on the type of flow and the type of path encoded by the centrality. A flow can be based on transfers, where each indivisible item goes from one node to another, like a package delivery going from the delivery site to the client's house. A second case is serial duplication, in which an item is replicated so that both the source and the target have it. An example is the propagation of information through gossip, with the information being propagated in a private way and with both the source and the target nodes being informed at the end of the process. The last case is parallel duplication, with the item being duplicated to several links at the same time, like a radio broadcast which provides the same information to many listeners at once.

Likewise, the type of path can be constrained to geodesics (shortest paths), paths (no vertex is visited more than once), trails (vertices can be visited multiple times, no edge is traversed more than once), or walks (vertices and edges can be visited/traversed multiple times).

Characterization by walk structure

An alternative classification can be derived from how the centrality is constructed. This again splits into two classes. Centralities are either radial or medial. Radial centralities count walks which start/end from the given vertex. The degree and eigenvalue centralities are examples of radial centralities, counting the number of walks of length one or length infinity. Medial centralities count walks which pass through the given vertex. The canonical example is Freeman's betweenness centrality, the number of shortest paths which pass through the given vertex.

Likewise, the counting can capture either the volume or the length of walks. Volume is the total number of walks of the given type. The three examples from the previous paragraph fall into this category. Length captures the distance from the given vertex to the remaining vertices in the graph. Closeness centrality, the total geodesic distance from a given vertex to all other vertices, is the best known example. Note that this classification is independent of the type of walk counted (i.e. walk, trail, path, geodesic).

Borgatti and Everett propose that this typology provides insight into how best to compare centrality measures. Centralities placed in the same box in this 2×2 classification are similar enough to make plausible alternatives; one can reasonably compare which is better for a given application. Measures from different boxes, however, are categorically distinct. Any evaluation of relative fitness can only occur within the context of predetermining which category is more applicable, rendering the comparison moot.

Radial-volume centralities exist on a spectrum

The characterization by walk structure shows that almost all centralities in wide use are radial-volume measures. These encode the belief that a vertex's centrality is a function of the centrality of the vertices it is associated with. Centralities distinguish themselves on how association is defined.

Bonacich showed that if association is defined in terms of walks, then a family of centralities can be defined based on the length of walk considered. Degree centrality counts walks of length one, while eigenvalue centrality counts walks of length infinity. Alternative definitions of association are also reasonable. Alpha centrality allows vertices to have an external source of influence. Estrada's subgraph centrality proposes only counting closed paths (triangles, squares, etc.).

The heart of such measures is the observation that powers of the graph's adjacency matrix gives the number of walks of length given by that power. Similarly, the matrix exponential is also closely related to the number of walks of a given length. An initial transformation of the adjacency matrix allows a different definition of the type of walk counted. Under either approach, the centrality of a vertex can be expressed as an infinite sum, either

${\displaystyle \sum _{k=0}^{\infty }A_{R}^{k}\beta ^{k}}$

for matrix powers or or

${\displaystyle \sum _{k=0}^{\infty }{\frac {(A_{R}\beta )^{k}}{k!}}}$

for matrix exponentials, where

• ${\displaystyle k}$ is walk length,
• ${\displaystyle A_{R}}$ is the transformed adjacency matrix, and
• ${\displaystyle \beta }$ is a discount parameter which ensures convergence of the sum.

Bonacich's family of measures does not transform the adjacency matrix. Alpha centrality replaces the adjacency matrix with its resolvent. Subgraph centrality replaces the adjacency matrix with its trace. A startling conclusion is that regardless of the initial transformation of the adjacency matrix, all such approaches have common limiting behavior. As ${\displaystyle \beta }$ approaches zero, the indices converge to degree centrality. As ${\displaystyle \beta }$ approaches its maximal value, the indices converge to eigenvalue centrality.

Game-theoretic centrality

The common feature of most of the aforementioned standard measures is that they assess the importance of a node by focusing only on the role that a node plays by itself. However, in many applications such an approach is inadequate because of synergies that may occur if the functioning of nodes is considered in groups.

For example, consider the problem of stopping an epidemic. Looking at above image of network, which nodes should we vaccinate? Based on previously described measures, we want to recognize nodes that are the most important in disease spreading. Approaches based only on centralities, that focus on individual features of nodes, may not be good idea. Nodes in the red square, individually cannot stop disease spreading, but considering them as a group, we clearly see that they can stop disease if it has started in nodes ${\displaystyle v_{1}}$, ${\displaystyle v_{4}}$, and ${\displaystyle v_{5}}$. Game-theoretic centralities try to consult described problems and opportunities, using tools from game-theory. The approach proposed in uses the Shapley value. Because of the time-complexity hardness of the Shapley value calculation, most efforts in this domain are driven into implementing new algorithms and methods which rely on a peculiar topology of the network or a special character of the problem. Such an approach may lead to reducing time-complexity from exponential to polynomial.

Similarly, the solution concept authority distribution () applies the Shapley-Shubik power index, rather than the Shapley value, to measure the bilateral direct influence between the players. The distribution is indeed a type of eigenvector centrality. It is used to sort big data objects in Hu (2020), such as ranking U.S. colleges.

Important limitations

Centrality indices have two important limitations, one obvious and the other subtle. The obvious limitation is that a centrality which is optimal for one application is often sub-optimal for a different application. Indeed, if this were not so, we would not need so many different centralities. An illustration of this phenomenon is provided by the Krackhardt kite graph, for which three different notions of centrality give three different choices of the most central vertex.

The more subtle limitation is the commonly held fallacy that vertex centrality indicates the relative importance of vertices. Centrality indices are explicitly designed to produce a ranking which allows indication of the most important vertices. This they do well, under the limitation just noted. They are not designed to measure the influence of nodes in general. Recently, network physicists have begun developing node influence metrics to address this problem.

The error is two-fold. Firstly, a ranking only orders vertices by importance, it does not quantify the difference in importance between different levels of the ranking. This may be mitigated by applying Freeman centralization to the centrality measure in question, which provide some insight to the importance of nodes depending on the differences of their centralization scores. Furthermore, Freeman centralization enables one to compare several networks by comparing their highest centralization scores.

Secondly, the features which (correctly) identify the most important vertices in a given network/application do not necessarily generalize to the remaining vertices. For the majority of other network nodes the rankings may be meaningless. This explains why, for example, only the first few results of a Google image search appear in a reasonable order. The pagerank is a highly unstable measure, showing frequent rank reversals after small adjustments of the jump parameter.

While the failure of centrality indices to generalize to the rest of the network may at first seem counter-intuitive, it follows directly from the above definitions. Complex networks have heterogeneous topology. To the extent that the optimal measure depends on the network structure of the most important vertices, a measure which is optimal for such vertices is sub-optimal for the remainder of the network.

Degree centrality

Historically first and conceptually simplest is degree centrality, which is defined as the number of links incident upon a node (i.e., the number of ties that a node has). The degree can be interpreted in terms of the immediate risk of a node for catching whatever is flowing through the network (such as a virus, or some information). In the case of a directed network (where ties have direction), we usually define two separate measures of degree centrality, namely indegree and outdegree. Accordingly, indegree is a count of the number of ties directed to the node and outdegree is the number of ties that the node directs to others. When ties are associated to some positive aspects such as friendship or collaboration, indegree is often interpreted as a form of popularity, and outdegree as gregariousness.

The degree centrality of a vertex ${\displaystyle v}$, for a given graph ${\displaystyle G:=(V,E)}$ with ${\displaystyle |V|}$ vertices and ${\displaystyle |E|}$ edges, is defined as

${\displaystyle C_{D}(v)=\deg(v)}$

Calculating degree centrality for all the nodes in a graph takes ${\displaystyle \Theta (V^{2})}$ in a dense adjacency matrix representation of the graph, and for edges takes ${\displaystyle \Theta (E)}$ in a sparse matrix representation.

The definition of centrality on the node level can be extended to the whole graph, in which case we are speaking of graph centralization. Let ${\displaystyle v*}$ be the node with highest degree centrality in ${\displaystyle G}$. Let ${\displaystyle X:=(Y,Z)}$ be the ${\displaystyle |Y|}$-node connected graph that maximizes the following quantity (with ${\displaystyle y*}$ being the node with highest degree centrality in ${\displaystyle X}$):

${\displaystyle H=\sum _{j=1}^{|Y|}}$

Correspondingly, the degree centralization of the graph ${\displaystyle G}$ is as follows:

${\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}}{H}}}$

The value of ${\displaystyle H}$ is maximized when the graph ${\displaystyle X}$ contains one central node to which all other nodes are connected (a star graph), and in this case

${\displaystyle H=(n-1)\cdot ((n-1)-1)=n^{2}-3n+2.}$

So, for any graph ${\displaystyle G:=(V,E),}$

${\displaystyle C_{D}(G)={\frac {\sum _{i=1}^{|V|}}{|V|^{2}-3|V|+2}}}$

Also, a new extensive global measure for degree centrality named Tendency to Make Hub (TMH) defines as follows:

${\displaystyle {\text{TMH}}={\frac {\sum _{i=1}^{|V|}\deg(v)^{2}}{\sum _{i=1}^{|V|}\deg(v)}}}$

where TMH increases by appearance of degree centrality in the network.

Closeness centrality

In a connected graph, the normalized closeness centrality (or closeness) of a node is the average length of the shortest path between the node and all other nodes in the graph. Thus the more central a node is, the closer it is to all other nodes.

Closeness was defined by Alex Bavelas (1950) as the reciprocal of the farness, that is ${\textstyle C_{B}(v)=(\sum _{u}d(u,v))^{-1}}$ where ${\displaystyle d(u,v)}$ is the distance between vertices u and v. However, when speaking of closeness centrality, people usually refer to its normalized form, given by the previous formula multiplied by ${\displaystyle N-1}$, where ${\displaystyle N}$ is the number of nodes in the graph

${\displaystyle C(v)={\frac {N-1}{\sum _{u}d(u,v)}}.}$

This normalisation allows comparisons between nodes of graphs of different sizes. For many graphs, there is a strong correlation between the inverse of closeness and the logarithm of degree, ${\displaystyle (C(v))^{-1}\approx -\alpha \ln(k_{v})+\beta }$ where ${\displaystyle k_{v}}$ is the degree of vertex v while α and β are constants for each network.

Taking distances from or to all other nodes is irrelevant in undirected graphs, whereas it can produce totally different results in directed graphs (e.g. a website can have a high closeness centrality from outgoing link, but low closeness centrality from incoming links).

Harmonic centrality

In a (not necessarily connected) graph, the harmonic centrality reverses the sum and reciprocal operations in the definition of closeness centrality:

${\displaystyle H(v)=\sum _{u|u\neq v}{\frac {1}{d(u,v)}}}$

where ${\displaystyle 1/d(u,v)=0}$ if there is no path from u to v. Harmonic centrality can be normalized by dividing by ${\displaystyle N-1}$, where ${\displaystyle N}$ is the number of nodes in the graph.

Harmonic centrality was proposed by Marchiori and Latora (2000) and then independently by Dekker (2005), using the name "valued centrality," and by Rochat (2009).

Betweenness centrality

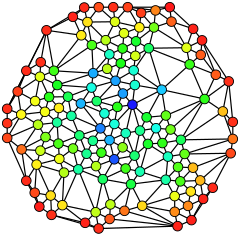
Betweenness is a centrality measure of a vertex within a graph (there is also edge betweenness, which is not discussed here). Betweenness centrality quantifies the number of times a node acts as a bridge along the shortest path between two other nodes. It was introduced as a measure for quantifying the control of a human on the communication between other humans in a social network by Linton Freeman. In his conception, vertices that have a high probability to occur on a randomly chosen shortest path between two randomly chosen vertices have a high betweenness.

The betweenness of a vertex ${\displaystyle v}$ in a graph ${\displaystyle G:=(V,E)}$ with ${\displaystyle V}$ vertices is computed as follows:

1. For each pair of vertices (s,t), compute the shortest paths between them.
2. For each pair of vertices (s,t), determine the fraction of shortest paths that pass through the vertex in question (here, vertex v).
3. Sum this fraction over all pairs of vertices (s,t).

More compactly the betweenness can be represented as:

${\displaystyle C_{B}(v)=\sum _{s\neq v\neq t\in V}{\frac {\sigma _{st}(v)}{\sigma _{st}}}}$

where ${\displaystyle \sigma _{st}}$ is total number of shortest paths from node ${\displaystyle s}$ to node ${\displaystyle t}$ and ${\displaystyle \sigma _{st}(v)}$ is the number of those paths that pass through ${\displaystyle v}$. The betweenness may be normalised by dividing through the number of pairs of vertices not including v, which for directed graphs is ${\displaystyle (n-1)(n-2)}$ and for undirected graphs is ${\displaystyle (n-1)(n-2)/2}$. For example, in an undirected star graph, the center vertex (which is contained in every possible shortest path) would have a betweenness of ${\displaystyle (n-1)(n-2)/2}$ (1, if normalised) while the leaves (which are contained in no shortest paths) would have a betweenness of 0.

From a calculation aspect, both betweenness and closeness centralities of all vertices in a graph involve calculating the shortest paths between all pairs of vertices on a graph, which requires ${\displaystyle O(V^{3})}$ time with the Floyd–Warshall algorithm. However, on sparse graphs, Johnson's algorithm may be more efficient, taking ${\displaystyle O(|V||E|+|V|^{2}\log |V|)}$ time. In the case of unweighted graphs the calculations can be done with Brandes' algorithm which takes ${\displaystyle O(|V||E|)}$ time. Normally, these algorithms assume that graphs are undirected and connected with the allowance of loops and multiple edges. When specifically dealing with network graphs, often graphs are without loops or multiple edges to maintain simple relationships (where edges represent connections between two people or vertices). In this case, using Brandes' algorithm will divide final centrality scores by 2 to account for each shortest path being counted twice.

Eigenvector centrality

Eigenvector centrality (also called eigencentrality) is a measure of the influence of a node in a network. It assigns relative scores to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes. Google's PageRank and the Katz centrality are variants of the eigenvector centrality.

Using the adjacency matrix to find eigenvector centrality

For a given graph ${\displaystyle G:=(V,E)}$ with ${\displaystyle |V|}$ number of vertices let ${\displaystyle A=(a_{v,t})}$ be the adjacency matrix, i.e. ${\displaystyle a_{v,t}=1}$ if vertex ${\displaystyle v}$ is linked to vertex ${\displaystyle t}$, and ${\displaystyle a_{v,t}=0}$ otherwise. The relative centrality score ${\displaystyle x_{v}}$ of vertex ${\displaystyle v}$ can be defined as the nonnegative solution over the set of vertices ${\displaystyle v\in V}$ to the equations:

${\displaystyle x_{v}={\frac {1}{\lambda }}\sum _{t\in M(v)}x_{t}={\frac {1}{\lambda }}\sum _{t\in G}a_{v,t}x_{t}}$

where ${\displaystyle M(v)}$ is a set of the neighbors of ${\displaystyle v}$ and ${\displaystyle \lambda }$ is a constant. With a small rearrangement this can be rewritten in vector notation as the eigenvector equation

${\displaystyle \mathbf {Ax} ={\lambda }\mathbf {x} }$.

In general, there will be many different eigenvalues ${\displaystyle \lambda }$ for which a non-zero eigenvector solution exists. Since the entries in the adjacency matrix are non-negative, there is a unique largest eigenvalue, which is real and positive, by the Perron–Frobenius theorem. This greatest eigenvalue results in the desired centrality measure. The ${\displaystyle v^{th}}$ component of the related eigenvector then gives the relative centrality score of the vertex ${\displaystyle v}$ in the network. The eigenvector is only defined up to a common factor, so only the ratios of the centralities of the vertices are well defined. To define an absolute score one must normalise the eigenvector, e.g., such that the sum over all vertices is 1 or the total number of vertices n. Power iteration is one of many eigenvalue algorithms that may be used to find this dominant eigenvector. Furthermore, this can be generalized so that the entries in A can be real numbers representing connection strengths, as in a stochastic matrix.

Katz centrality

Katz centrality is a generalization of degree centrality. Degree centrality measures the number of direct neighbors, and Katz centrality measures the number of all nodes that can be connected through a path, while the contributions of distant nodes are penalized. Mathematically, it is defined as

${\displaystyle x_{i}=\sum _{k=1}^{\infty }\sum _{j=1}^{N}\alpha ^{k}(A^{k})_{ji}}$

where ${\displaystyle \alpha }$ is an attenuation factor in ${\displaystyle (0,1)}$.

Katz centrality can be viewed as a variant of eigenvector centrality. Another form of Katz centrality is

${\displaystyle x_{i}=\alpha \sum _{j=1}^{N}a_{ij}(x_{j}+1).}$

Compared to the expression of eigenvector centrality, ${\displaystyle x_{j}}$ is replaced by ${\displaystyle x_{j}+1.}$

It is shown that the principal eigenvector (associated with the largest eigenvalue of ${\displaystyle A}$, the adjacency matrix) is the limit of Katz centrality as ${\displaystyle \alpha }$ approaches ${\displaystyle {\tfrac {1}{\lambda }}}$ from below.

PageRank centrality

PageRank satisfies the following equation

${\displaystyle x_{i}=\alpha \sum _{j}a_{ji}{\frac {x_{j}}{L(j)}}+{\frac {1-\alpha }{N}},}$

where

${\displaystyle L(j)=\sum _{i}a_{ji}}$

is the number of neighbors of node ${\displaystyle j}$ (or number of outbound links in a directed graph). Compared to eigenvector centrality and Katz centrality, one major difference is the scaling factor ${\displaystyle L(j)}$. Another difference between PageRank and eigenvector centrality is that the PageRank vector is a left hand eigenvector (note the factor ${\displaystyle a_{ji}}$ has indices reversed).

Percolation centrality

A slew of centrality measures exist to determine the ‘importance’ of a single node in a complex network. However, these measures quantify the importance of a node in purely topological terms, and the value of the node does not depend on the ‘state’ of the node in any way. It remains constant regardless of network dynamics. This is true even for the weighted betweenness measures. However, a node may very well be centrally located in terms of betweenness centrality or another centrality measure, but may not be ‘centrally’ located in the context of a network in which there is percolation. Percolation of a ‘contagion’ occurs in complex networks in a number of scenarios. For example, viral or bacterial infection can spread over social networks of people, known as contact networks. The spread of disease can also be considered at a higher level of abstraction, by contemplating a network of towns or population centres, connected by road, rail or air links. Computer viruses can spread over computer networks. Rumours or news about business offers and deals can also spread via social networks of people. In all of these scenarios, a ‘contagion’ spreads over the links of a complex network, altering the ‘states’ of the nodes as it spreads, either recoverable or otherwise. For example, in an epidemiological scenario, individuals go from ‘susceptible’ to ‘infected’ state as the infection spreads. The states the individual nodes can take in the above examples could be binary (such as received/not received a piece of news), discrete (susceptible/infected/recovered), or even continuous (such as the proportion of infected people in a town), as the contagion spreads. The common feature in all these scenarios is that the spread of contagion results in the change of node states in networks. Percolation centrality (PC) was proposed with this in mind, which specifically measures the importance of nodes in terms of aiding the percolation through the network. This measure was proposed by Piraveenan et al.

Percolation centrality is defined for a given node, at a given time, as the proportion of ‘percolated paths’ that go through that node. A ‘percolated path’ is a shortest path between a pair of nodes, where the source node is percolated (e.g., infected). The target node can be percolated or non-percolated, or in a partially percolated state.

${\displaystyle PC^{t}(v)={\frac {1}{N-2}}\sum _{s\neq v\neq r}{\frac {\sigma _{sr}(v)}{\sigma _{sr}}}{\frac {{x^{t}}_{s}}{{\sum {}-{x^{t}}_{v}}}}$

where ${\displaystyle \sigma _{sr}}$ is total number of shortest paths from node ${\displaystyle s}$ to node ${\displaystyle r}$ and ${\displaystyle \sigma _{sr}(v)}$ is the number of those paths that pass through ${\displaystyle v}$. The percolation state of the node ${\displaystyle i}$ at time ${\displaystyle t}$ is denoted by ${\displaystyle {x^{t}}_{i}}$ and two special cases are when ${\displaystyle {x^{t}}_{i}=0}$ which indicates a non-percolated state at time ${\displaystyle t}$ whereas when ${\displaystyle {x^{t}}_{i}=1}$ which indicates a fully percolated state at time ${\displaystyle t}$. The values in between indicate partially percolated states ( e.g., in a network of townships, this would be the percentage of people infected in that town).

The attached weights to the percolation paths depend on the percolation levels assigned to the source nodes, based on the premise that the higher the percolation level of a source node is, the more important are the paths that originate from that node. Nodes which lie on shortest paths originating from highly percolated nodes are therefore potentially more important to the percolation. The definition of PC may also be extended to include target node weights as well. Percolation centrality calculations run in ${\displaystyle O(NM)}$ time with an efficient implementation adopted from Brandes' fast algorithm and if the calculation needs to consider target nodes weights, the worst case time is ${\displaystyle O(N^{3})}$.

Cross-clique centrality

Cross-clique centrality of a single node in a complex graph determines the connectivity of a node to different cliques. A node with high cross-clique connectivity facilitates the propagation of information or disease in a graph. Cliques are subgraphs in which every node is connected to every other node in the clique. The cross-clique connectivity of a node ${\displaystyle v}$ for a given graph ${\displaystyle G:=(V,E)}$ with ${\displaystyle |V|}$ vertices and ${\displaystyle |E|}$ edges, is defined as ${\displaystyle X(v)}$ where ${\displaystyle X(v)}$ is the number of cliques to which vertex ${\displaystyle v}$ belongs. This measure was used by Faghani in 2013 but was first proposed by Everett and Borgatti in 1998 where they called it clique-overlap centrality.

Freeman centralization

The centralization of any network is a measure of how central its most central node is in relation to how central all the other nodes are. Centralization measures then (a) calculate the sum in differences in centrality between the most central node in a network and all other nodes; and (b) divide this quantity by the theoretically largest such sum of differences in any network of the same size. Thus, every centrality measure can have its own centralization measure. Defined formally, if ${\displaystyle C_{x}(p_{i})}$ is any centrality measure of point ${\displaystyle i}$, if ${\displaystyle C_{x}(p_{*})}$ is the largest such measure in the network, and if:

${\displaystyle \max \sum _{i=1}^{N}(C_{x}(p_{*})-C_{x}(p_{i}))}$

is the largest sum of differences in point centrality ${\displaystyle C_{x}}$ for any graph with the same number of nodes, then the centralization of the network is:

${\displaystyle C_{x}={\frac {\sum _{i=1}^{N}(C_{x}(p_{*})-C_{x}(p_{i}))}{\max \sum _{i=1}^{N}(C_{x}(p_{*})-C_{x}(p_{i}))}}.}$

The concept is due to Linton Freeman.

Dissimilarity-based centrality measures

In order to obtain better results in the ranking of the nodes of a given network, in are used dissimilarity measures (specific to the theory of classification and data mining) to enrich the centrality measures in complex networks. This is illustrated with eigenvector centrality, calculating the centrality of each node through the solution of the eigenvalue problem

${\displaystyle W\mathbf {c} =\lambda \mathbf {c} }$

where ${\displaystyle W_{ij}=A_{ij}D_{ij}}$ (coordinate-to-coordinate product) and ${\displaystyle D_{ij}}$ is an arbitrary dissimilarity matrix, defined through a dissimilarity measure, e.g., Jaccard dissimilarity given by

${\displaystyle D_{ij}=1-{\dfrac {|V^{+}(i)\cap V^{+}(j)|}{|V^{+}(i)\cup V^{+}(j)|}}}$

Where this measure permits us to quantify the topological contribution (which is why is called contribution centrality) of each node to the centrality of a given node, having more weight/relevance those nodes with greater dissimilarity, since these allow to the given node access to nodes that which themselves can not access directly.

Is noteworthy that ${\displaystyle W}$ is non-negative because ${\displaystyle A}$ and ${\displaystyle D}$ are non-negative matrices, so we can use the Perron–Frobenius theorem to ensure that the above problem has a unique solution for λ = λ_max with c non-negative, allowing us to infer the centrality of each node in the network. Therefore, the centrality of the i-th node is

${\displaystyle c_{i}={\dfrac {1}{n}}\sum _{j=1}^{n}W_{ij}c_{j},\,\,\,\,\,\,i=1,\cdots ,n}$

where ${\displaystyle n}$ is the number of the nodes in the network. Several dissimilarity measures and networks were tested in obtaining improved results in the studied cases.

Centrality measures used in transportation networks

Transportation networks such as road networks and railway networks are studied extensively in transportation science and urban planning. A number of recent studies have focused on using centrality measures to analyze transportation networks. While many of these studies simply use generic centrality measures such as Betweenness Centrality, custom centrality measures have also been defined specifically for transportation network analysis. Prominent among them is Transportation Centrality.

Transportation centrality measures the summation of the proportions of paths from pairs of nodes in a network which go through the node under consideration. In this respect it is similar to Betweenness Centrality. However, unlike Betweenness Centrality which considers only shortest paths, Transportation Centrality considers all possible paths between a pair of nodes. Therefore, Transportation Centrality is a generic version of Betweenness Centrality, and under certain conditions, it indeed reduces to Betweenness Centrality.

Transportation Centrality of a given node v is defined as:

${\displaystyle TC(v)=1/((N-1)(N-2))\Sigma _{s\neq v\neq t}{\frac {\Sigma _{i\in P_{s,t}^{v}}e^{-\beta C_{s,t}^{i}}}{\Sigma _{j\in P_{s,t}^{v}}e^{-\beta C_{s,t}^{j}}}}}$

See also

• Alpha centrality
• Core–periphery structure
• Distance in graphs

Notes and references

1. van den Heuvel MP, Sporns O (December 2013). "Network hubs in the human brain". Trends in Cognitive Sciences. 17 (12): 683–96. doi:10.1016/j.tics.2013.09.012. PMID 24231140. S2CID 18644584.
2. ^ Saberi M, Khosrowabadi R, Khatibi A, Misic B, Jafari G (January 2021). "Topological impact of negative links on the stability of resting-state brain network". Scientific Reports. 11 (1): 2176. Bibcode:2021NatSR..11.2176S. doi:10.1038/s41598-021-81767-7. PMC 7838299. PMID 33500525.
3. Newman, M.E.J. 2010. Networks: An Introduction. Oxford, UK: Oxford University Press.
4. ^ Bonacich, Phillip (1987). "Power and Centrality: A Family of Measures". American Journal of Sociology. 92 (5): 1170–1182. doi:10.1086/228631. S2CID 145392072.
5. ^ Borgatti, Stephen P. (2005). "Centrality and Network Flow". Social Networks. 27: 55–71. CiteSeerX 10.1.1.387.419. doi:10.1016/j.socnet.2004.11.008.
6. ^ Christian F. A. Negre, Uriel N. Morzan, Heidi P. Hendrickson, Rhitankar Pal, George P. Lisi, J. Patrick Loria, Ivan Rivalta, Junming Ho, Victor S. Batista. (2018). "Eigenvector centrality for characterization of protein allosteric pathways". Proceedings of the National Academy of Sciences. 115 (52): E12201–E12208. arXiv:1706.02327. Bibcode:2018PNAS..11512201N. doi:10.1073/pnas.1810452115. PMC 6310864. PMID 30530700.{{cite journal}}: CS1 maint: multiple names: authors list (link)
7. ^ Borgatti, Stephen P.; Everett, Martin G. (2006). "A Graph-Theoretic Perspective on Centrality". Social Networks. 28 (4): 466–484. doi:10.1016/j.socnet.2005.11.005.
8. ^ Benzi, Michele; Klymko, Christine (2013). "A matrix analysis of different centrality measures". SIAM Journal on Matrix Analysis and Applications. 36 (2): 686–706. arXiv:1312.6722. doi:10.1137/130950550. S2CID 7088515.
9. Michalak, Aadithya, Szczepański, Ravindran, & Jennings arXiv:1402.0567
10. Hu, Xingwei; Shapley, Lloyd (2003). "On Authority Distributions in Organizations". Games and Economic Behavior. 45: 132–170. doi:10.1016/s0899-8256(03)00130-1.
11. Hu, Xingwei (2020). "Sorting big data by revealed preference with application to college ranking". Journal of Big Data. 7. arXiv:2003.12198. doi:10.1186/s40537-020-00300-1.
12. Krackhardt, David (June 1990). "Assessing the Political Landscape: Structure, Cognition, and Power in Organizations". Administrative Science Quarterly. 35 (2): 342–369. doi:10.2307/2393394. JSTOR 2393394.
13. ^ Freeman, Linton C. (1979), "centrality in social networks: Conceptual clarification" (PDF), Social Networks, 1 (3): 215–239, CiteSeerX 10.1.1.227.9549, doi:10.1016/0378-8733(78)90021-7, S2CID 751590, archived from the original (PDF) on 2016-02-22, retrieved 2014-07-31
14. ^ Lawyer, Glenn (2015). "Understanding the spreading power of all nodes in a network: a continuous-time perspective". Sci Rep. 5: 8665. arXiv:1405.6707. Bibcode:2015NatSR...5E8665L. doi:10.1038/srep08665. PMC 4345333. PMID 25727453.
15. da Silva, Renato; Viana, Matheus; da F. Costa, Luciano (2012). "Predicting epidemic outbreak from individual features of the spreaders". J. Stat. Mech.: Theory Exp. 2012 (7): P07005. arXiv:1202.0024. Bibcode:2012JSMTE..07..005A. doi:10.1088/1742-5468/2012/07/p07005. S2CID 2530998.
16. Bauer, Frank; Lizier, Joseph (2012). "Identifying influential spreaders and efficiently estimating infection numbers in epidemic models: A walk counting approach". Europhys Lett. 99 (6): 68007. arXiv:1203.0502. Bibcode:2012EL.....9968007B. doi:10.1209/0295-5075/99/68007. S2CID 9728486.
17. Sikic, Mile; Lancic, Alen; Antulov-Fantulin, Nino; Stefanic, Hrvoje (2013). "Epidemic centrality -- is there an underestimated epidemic impact of network peripheral nodes?". The European Physical Journal B. 86 (10): 1–13. arXiv:1110.2558. Bibcode:2013EPJB...86..440S. doi:10.1140/epjb/e2013-31025-5. S2CID 12052238.
18. Ghoshal, G.; Barabsi, A L (2011). "Ranking stability and super-stable nodes in complex networks". Nat Commun. 2: 394. Bibcode:2011NatCo...2..394G. doi:10.1038/ncomms1396. PMID 21772265.
19. Freeman, Linton C. "Centrality in social networks conceptual clarification." Social networks 1.3 (1979): 215–239.
20. Alex Bavelas. Communication patterns in task-oriented groups. J. Acoust. Soc. Am, 22(6):725–730, 1950.
21. Sabidussi, G (1966). "The centrality index of a graph". Psychometrika. 31 (4): 581–603. doi:10.1007/bf02289527. hdl:10338.dmlcz/101401. PMID 5232444. S2CID 119981743.
22. Evans, Tim S.; Chen, Bingsheng (2022). "Linking the network centrality measures closeness and degree". Communications Physics. 5 (1): 172. arXiv:2108.01149. Bibcode:2022CmPhy...5..172E. doi:10.1038/s42005-022-00949-5. ISSN 2399-3650. S2CID 236881169.
23. Marchiori, Massimo; Latora, Vito (2000), "Harmony in the small-world", Physica A: Statistical Mechanics and Its Applications, 285 (3–4): 539–546, arXiv:cond-mat/0008357, Bibcode:2000PhyA..285..539M, doi:10.1016/s0378-4371(00)00311-3, S2CID 10523345
24. Dekker, Anthony (2005). "Conceptual Distance in Social Network Analysis". Journal of Social Structure. 6 (3). Archived from the original on 2020-12-04. Retrieved 2017-02-18.
25. Yannick Rochat. Closeness centrality extended to unconnected graphs: The harmonic centrality index (PDF). Applications of Social Network Analysis, ASNA 2009. Archived (PDF) from the original on 2017-08-16. Retrieved 2017-02-19.
26. Freeman, Linton (1977). "A set of measures of centrality based upon betweenness". Sociometry. 40 (1): 35–41. doi:10.2307/3033543. JSTOR 3033543.
27. ^ Brandes, Ulrik (2001). "A faster algorithm for betweenness centrality" (PDF). Journal of Mathematical Sociology. 25 (2): 163–177. CiteSeerX 10.1.1.11.2024. doi:10.1080/0022250x.2001.9990249. hdl:10983/23603. S2CID 13971996. Archived from the original on March 4, 2016. Retrieved October 11, 2011.
28. ^ M. E. J. Newman (2016). "The mathematics of networks" (PDF). In Durlauf, Steven; Blume, Lawrence E. (eds.). The New Palgrave Dictionary of Economics (2nd ed.). Springer. pp. 465ff. Archived (PDF) from the original on 2021-01-22. Retrieved 2006-11-09.
29. ^ Austin, David (December 2006). "How Google Finds Your Needle in the Web's Haystack". AMS Feature Column. American Mathematical Society. Archived from the original on 2018-01-11. Retrieved 2011-08-24.
30. Katz, L. 1953. A New Status Index Derived from Sociometric Index. Psychometrika, 39–43.
31. Bonacich, P (1991). "Simultaneous group and individual centralities". Social Networks. 13 (2): 155–168. doi:10.1016/0378-8733(91)90018-o.
32. How does Google rank webpages? Archived January 31, 2012, at the Wayback Machine 20Q: About Networked Life
33. Piraveenan, M.; Prokopenko, M.; Hossain, L. (2013). "Percolation Centrality: Quantifying Graph-Theoretic Impact of Nodes during Percolation in Networks". PLOS ONE. 8 (1): e53095. Bibcode:2013PLoSO...853095P. doi:10.1371/journal.pone.0053095. PMC 3551907. PMID 23349699.
34. Faghani, Mohamamd Reza (2013). "A Study of XSS Worm Propagation and Detection Mechanisms in Online Social Networks". IEEE Transactions on Information Forensics and Security. 8 (11): 1815–1826. doi:10.1109/TIFS.2013.2280884. S2CID 13587900.
35. Alvarez-Socorro, A. J.; Herrera-Almarza, G. C.; González-Díaz, L. A. (2015-11-25). "Eigencentrality based on dissimilarity measures reveals central nodes in complex networks". Scientific Reports. 5: 17095. Bibcode:2015NatSR...517095A. doi:10.1038/srep17095. PMC 4658528. PMID 26603652.
36. Alvarez-Socorro, A.J.; Herrera-Almarza; González-Díaz, L. A. "Supplementary Information for Eigencentrality based on dissimilarity measures reveals central nodes in complex networks" (PDF). Nature Publishing Group. Archived (PDF) from the original on 2016-03-07. Retrieved 2015-12-29.
37. ^ Piraveenan, Mahendra; Saripada, Naressa Belle (2023). "Transportation Centrality: Quantifying the Relative Importance of Nodes in Transportation Networks Based on Traffic Modeling". IEEE Access. 11: 142214–142234. Bibcode:2023IEEEA..11n2214P. doi:10.1109/ACCESS.2023.3339121. ISSN 2169-3536.

Further reading

• Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) Network Analysis: Methodological Foundations, pp. 16–61, LNCS 3418, Springer-Verlag.

• Graph theory
• Graph algorithms
• Algebraic graph theory
• Networks
• Network analysis
• Network theory
• Graph distance