Misplaced Pages

Coenergy

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Graphical definition of coenergy

In physics and engineering, Coenergy (or co-energy) is a non-physical quantity, measured in energy units, used in theoretical analysis of energy in physical systems.

The concept of co-energy can be applied to many conservative systems (inertial mechanical, electromagnetic, etc.), which can be described by a linear relationship between the input and stored energy.

The co-energy analysis techniques cannot be applied to non-linear systems. However, small nonlinearities are often neglected by linearisation of the problems.

Example - magnetic coenergy

Consider a system with a single coil and a non-moving armature (i.e. no mechanical work is done). Hence, all of the electric energy supplied to the device is stored in the magnetic field. d W input = d W stored ( d W mechanical = 0 ) {\displaystyle dW_{\text{input}}=dW_{\text{stored}}\qquad (dW_{\text{mechanical}}=0)}

where (e is the voltage, i is the current, and λ {\displaystyle \lambda } is the flux linkage): d W input = e i d t {\displaystyle dW_{\text{input}}=ei\,dt} d W stored = i d λ {\displaystyle dW_{\text{stored}}=i\,d\lambda } therefore d W stored = e i d t = i d λ {\displaystyle dW_{\text{stored}}=ei\,dt=i\,d\lambda }

For a general problem the relationship i − λ {\displaystyle i-\lambda } is non-linear (see also magnetic hysteresis).

If there is a finite change in flux linkage from one value to another (e.g. from λ 1 {\displaystyle \lambda _{1}} to λ 2 {\displaystyle \lambda _{2}} ), it can be calculated as: Δ W stored = ∫ λ 1 λ 2 i ( λ ) d λ {\displaystyle \Delta W_{\text{stored}}=\int _{\lambda _{1}}^{\lambda _{2}}i(\lambda )\,d\lambda }

(If the changes are cyclic there will be losses for hysteresis and eddy currents. The additional energy for this would be taken from the input energy, so that the flux linkage to the coil is not affected by the losses and the coil can be treated as an ideal lossless coil. Such system is therefore conservative.)

For calculations either the flux linkage λ {\displaystyle \lambda } or the current i can be used as the independent variable.

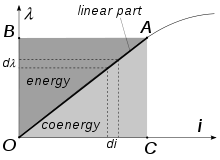
The total energy stored in the system is equal to the area OABO, which is in turn equal to OACO, therefore: E n e r g y = Area ⁡ ( O A B O ) = W stored = ∫ 0 λ i ( λ ) d λ {\displaystyle \mathrm {Energy} =\operatorname {Area} (OABO)=W_{\text{stored}}=\int _{0}^{\lambda }i(\lambda )\,d\lambda } C o e n e r g y = Area ⁡ ( O A C O ) = W stored ′ = ∫ 0 i λ ( i ) d i {\displaystyle \mathrm {Coenergy} =\operatorname {Area} (OACO)=W'_{\text{stored}}=\int _{0}^{i}\lambda (i)\,di}

For linear lossless systems the coenergy is equal in value to the stored energy. The coenergy has no real physical meaning, but it is useful in calculating mechanical forces in electromagnetic systems. To distinguish it from the "real" energy in calculations it is usually marked with an apostrophe.

The total area of the rectangle OCABO is equal to the sum of the two triangles (energy + coenergy), so: Area ⁡ ( O C A B O ) = Area ⁡ ( O A B O ) + Area ⁡ ( O A C O ) {\displaystyle \operatorname {Area} (OCABO)=\operatorname {Area} (OABO)+\operatorname {Area} (OACO)}

Hence for at a given operating point with current i and flux linkage λ {\displaystyle \lambda } : E n e r g y ( W ) + C o e n e r g y ( W ′ ) = i λ {\displaystyle \mathrm {Energy} (W)+\mathrm {Coenergy} (W')=i\lambda }

The self inductance is defined as flux linkage over current: L = λ i {\displaystyle L={\frac {\lambda }{i}}} and the energy stored in a coil is: W energy = 1 2 λ 2 L = 1 2 L i 2 {\displaystyle W_{\text{energy}}={\frac {1}{2}}{\frac {\lambda ^{2}}{L}}={\frac {1}{2}}Li^{2}}

In a magnetic circuit with a movable-armature the inductance L(x) will be a function of position x.

Therefore the field energy can be written as a function of two mathematically independent variables λ {\displaystyle \lambda } and x: W ( λ , x ) energy = 1 2 λ 2 L ( x ) {\displaystyle W(\lambda ,x)_{\text{energy}}={\frac {1}{2}}\,{\frac {\lambda ^{2}}{L(x)}}}

And the coenergy is a function of two independent variables i and x: W ′ ( i , x ) coenergy = 1 2 L ( x ) i 2 {\displaystyle W'(i,x)_{\text{coenergy}}={\frac {1}{2}}L(x)i^{2}}

The last two expressions are general equations for energy and coenergy in magnetostatic system.

Applications of coenergy theory

The concept of coenergy is practically used for instance in finite element analysis for calculations of mechanical forces between magnetized parts.

References

  1. ^ U.A. Bakshi, M.V. Bakshi, Electrical Machines - I, Technical Publications Pune, India, May 2006, ISBN 81-8431-225-3, page 11
Category: