Misplaced Pages

In proof theory, a coherent space (also coherence space) is a concept introduced in the semantic study of linear logic.

Let a set C be given. Two subsets S,T ⊆ C are said to be orthogonal, written S ⊥ T, if S ∩ T is ∅ or a singleton. The dual of a family F ⊆ ℘(C) is the family F of all subsets S ⊆ C orthogonal to every member of F, i.e., such that S ⊥ T for all T ∈ F. A coherent space F over C is a family of C-subsets for which F = (F ) .

In Proofs and Types coherent spaces are called coherence spaces. A footnote explains that although in the French original they were espaces cohérents, the coherence space translation was used because spectral spaces are sometimes called coherent spaces.

Definitions

As defined by Jean-Yves Girard, a coherence space ${\displaystyle {\mathcal {A}}}$ is a collection of sets satisfying down-closure and binary completeness in the following sense:

• Down-closure: all subsets of a set in ${\displaystyle {\mathcal {A}}}$ remain in ${\displaystyle {\mathcal {A}}}$: ${\displaystyle a'\subset a\in {\mathcal {A}}\implies a'\in {\mathcal {A}}}$
• Binary completeness: for any subset ${\displaystyle M}$ of ${\displaystyle {\mathcal {A}}}$, if the pairwise union of any of its elements is in ${\displaystyle {\mathcal {A}}}$, then so is the union of all the elements of ${\displaystyle M}$: ${\displaystyle \forall M\subset {\mathcal {A}},\left((\forall a_{1},a_{2}\in M,\ a_{1}\cup a_{2}\in {\mathcal {A}})\implies \bigcup M\in {\mathcal {A}}\right)}$

The elements of the sets in ${\displaystyle {\mathcal {A}}}$ are known as tokens, and they are the elements of the set ${\displaystyle |{\mathcal {A}}|=\bigcup {\mathcal {A}}=\{\alpha |\{\alpha \}\in {\mathcal {A}}\}}$.

Coherence spaces correspond one-to-one with (undirected) graphs (in the sense of a bijection from the set of coherence spaces to that of undirected graphs). The graph corresponding to ${\displaystyle {\mathcal {A}}}$ is called the web of ${\displaystyle {\mathcal {A}}}$ and is the graph induced a reflexive, symmetric relation ${\displaystyle \sim }$ over the token space ${\displaystyle |{\mathcal {A}}|}$ of ${\displaystyle {\mathcal {A}}}$ known as coherence modulo ${\displaystyle {\mathcal {A}}}$ defined as:$${\displaystyle a\sim b\iff \{a,b\}\in {\mathcal {A}}}$$In the web of ${\displaystyle {\mathcal {A}}}$, nodes are tokens from ${\displaystyle |{\mathcal {A}}|}$ and an edge is shared between nodes ${\displaystyle a}$ and ${\displaystyle b}$ when ${\displaystyle a\sim b}$ (i.e. ${\displaystyle \{a,b\}\in {\mathcal {A}}}$.) This graph is unique for each coherence space, and in particular, elements of ${\displaystyle {\mathcal {A}}}$ are exactly the cliques of the web of ${\displaystyle {\mathcal {A}}}$ i.e. the sets of nodes whose elements are pairwise adjacent (share an edge.)

Coherence spaces as types

Coherence spaces can act as an interpretation for types in type theory where points of a type ${\displaystyle {\mathcal {A}}}$ are points of the coherence space ${\displaystyle {\mathcal {A}}}$. This allows for some structure to be discussed on types. For instance, each term ${\displaystyle a}$ of a type ${\displaystyle {\mathcal {A}}}$ can be given a set of finite approximations ${\displaystyle I}$ which is in fact, a directed set with the subset relation. With ${\displaystyle a}$ being a coherent subset of the token space ${\displaystyle |{\mathcal {A}}|}$ (i.e. an element of ${\displaystyle {\mathcal {A}}}$), any element of ${\displaystyle I}$ is a finite subset of ${\displaystyle a}$ and therefore also coherent, and we have ${\displaystyle a=\bigcup a_{i},a_{i}\in I.}$

Stable functions

Functions between types ${\displaystyle {\mathcal {A}}\to {\mathcal {B}}}$ are seen as stable functions between coherence spaces. A stable function is defined to be one which respects approximants and satisfies a certain stability axiom. Formally, ${\displaystyle F:{\mathcal {A}}\to {\mathcal {B}}}$ is a stable function when

1. It is monotone with respect to the subset order (respects approximation, categorically, is a functor over the poset ${\displaystyle {\mathcal {A}}}$): ${\displaystyle a'\subset a\in {\mathcal {A}}\implies F(a')\subset F(a).}$
2. It is continuous (categorically, preserves filtered colimits): ${\textstyle F(\bigcup _{i\in I}^{\uparrow }a_{i})=\bigcup _{i\in I}^{\uparrow }F(a_{i})}$ where ${\textstyle \bigcup _{i\in I}^{\uparrow }}$ is the directed union over ${\displaystyle I}$, the set of finite approximants of ${\displaystyle a}$.
3. It is stable: ${\displaystyle a_{1}\cup a_{2}\in {\mathcal {A}}\implies F(a_{1}\cap a_{2})=F(a_{1})\cap F(a_{2}).}$ Categorically, this means that it preserves the pullback:

   

Product space

In order to be considered stable, functions of two arguments must satisfy the criterion 3 above in this form: $${\displaystyle a_{1}\cup a_{2}\in {\mathcal {A}}\land b_{1}\cup b_{2}\in {\mathcal {B}}\implies F(a_{1}\cap a_{2},b_{1}\cap b_{2})=F(a_{1},b_{1})\cap F(a_{2},b_{2})}$$which would mean that in addition to stability in each argument alone, the pullback

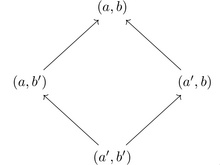
is preserved with stable functions of two arguments. This leads to the definition of a product space ${\displaystyle {\mathcal {A}}\ \&\ {\mathcal {B}}}$ which makes a bijection between stable binary functions (functions of two arguments) and stable unary functions (one argument) over the product space. The product coherence space is a product in the categorical sense i.e. it satisfies the universal property for products. It is defined by the equations:

• ${\displaystyle |{\mathcal {A}}\ \&\ {\mathcal {B}}|=|{\mathcal {A}}|+|{\mathcal {B}}|=(\{1\}\times |{\mathcal {A}}|)\cup (\{2\}\times |{\mathcal {B}}|)}$ (i.e. the set of tokens of ${\displaystyle {\mathcal {A}}\ \&\ {\mathcal {B}}}$ is the coproduct (or disjoint union) of the token sets of ${\displaystyle {\mathcal {A}}}$ and ${\displaystyle {\mathcal {B}}}$.
• Tokens from differents sets are always coherent and tokens from the same set are coherent exactly when they are coherent in that set.
  • ${\displaystyle (1,\alpha )\sim _{{\mathcal {A}}\ \&\ {\mathcal {B}}}(1,\alpha ')\iff \alpha \sim _{\mathcal {A}}\alpha '}$
  • ${\displaystyle (2,\beta )\sim _{{\mathcal {A}}\ \&\ {\mathcal {B}}}(2,\beta ')\iff \beta \sim _{\mathcal {B}}\beta '}$
  • ${\displaystyle (1,\alpha )\sim _{{\mathcal {A}}\ \&\ {\mathcal {B}}}(2,\beta ),\forall \alpha \in |{\mathcal {A}}|,\beta \in |{\mathcal {B}}|}$

References

• Girard, J.-Y.; Lafont, Y.; Taylor, P. (1989), Proofs and types (PDF), Cambridge University Press.
• Girard, J.-Y. (2004), "Between logic and quantic: a tract", in Ehrhard; Girard; Ruet; et al. (eds.), Linear logic in computer science (PDF), Cambridge University Press.

This mathematical logic-related article is a stub. You can help Misplaced Pages by expanding it.

• v
• t
• e

• Mathematical logic
• Mathematical logic stubs