| This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (February 2017) (Learn how and when to remove this message) |
Turbulent flows are complex multi-scale and chaotic motions that need to be classified into more elementary components, referred to coherent turbulent structures. Such a structure must have temporal coherence, i.e. it must persist in its form for long enough periods that the methods of time-averaged statistics can be applied. Coherent structures are typically studied on very large scales, but can be broken down into more elementary structures with coherent properties of their own, such examples include hairpin vortices. Hairpins and coherent structures have been studied and noticed in data since the 1930s, and have been since cited in thousands of scientific papers and reviews.

Flow visualization experiments, using smoke and dye as tracers, have been historically used to simulate coherent structures and verify theories, but computer models are now the dominant tools widely used in the field to verify and understand the formation, evolution, and other properties of such structures. The kinematic properties of these motions include size, scale, shape, vorticity, energy, and the dynamic properties govern the way coherent structures grow, evolve, and decay. Most coherent structures are studied only within the confined forms of simple wall turbulence, which approximates the coherence to be steady, fully developed, incompressible, and with a zero pressure gradient in the boundary layer. Although such approximations depart from reality, they contain sufficient parameters needed to understand turbulent coherent structures in a highly conceptual degree.
History and discovery
The presence of organized motions and structures in turbulent shear flows was apparent for a long time, and has been additionally implied by mixing length hypothesis even before the concept was explicitly stated in literature. There were also early correlation data found by measuring jets and turbulent wakes, particularly by Corrsin and Roshko. Hama's hydrogen bubble technique, which used flow visualization to observe the structures, received wide spread attention and many researchers followed up including Kline. Flow visualization is a laboratory experimental technique that is used to visualize and understand the structures of turbulent shear flows. With a much better understanding of coherent structures, it is now possible to discover and recognize many coherent structures in previous flow-visualization pictures collected of various turbulent flows taken decades ago. Computer simulations are now being the dominant tool for understanding and visualizing coherent flow structures. The ability to compute the necessary time-dependent Navier–Stokes equations produces graphic presentations at a much more sophisticated level, and can additionally be visualized at different planes and resolutions, exceeding the expected sizes and speeds previously generated in laboratory experiments. However, controlled flow visualization experiments are still necessary to direct, develop, and validate the numerical simulations now dominant in the field.
Definition
A turbulent flow is a flow regime in fluid dynamics where fluid velocity varies significantly and irregularly in both position and time. Furthermore, a coherent structure is defined as a turbulent flow whose vorticity expression, which is usually stochastic, contains orderly components that can be described as being instantaneously coherent over the spatial extent of the flow structure. In other words, underlying the three-dimensional chaotic vorticity expressions typical of turbulent flows, there is an organized component of that vorticity which is phase-correlated over the entire space of the structure. The instantaneously space and phase correlated vorticity found within the coherent structure expressions can be defined as coherent vorticity, hence making coherent vorticity the main characteristic identifier for coherent structures. Another characteristic inherent in turbulent flows is their intermittency, but intermittency is a very poor identifier of the boundaries of a coherent structure, hence it is generally accepted that the best way to characterize the boundary of a structure is by identifying and defining the boundary of the coherent vorticity.
By defining and identifying coherent structure in this manner, turbulent flows can be decomposed into coherent structures and incoherent structures depending on their coherence, particularly their correlations with their vorticity. Hence, similarly organized events in an ensemble average of organized events can be defined as a coherent structure, and whatever events not identified as similar or phase and space aligned in the ensemble average is an incoherent turbulent structure.
Other attempts at defining a coherent structure can be done through examining the correlation between their momenta or pressure and their turbulent flows. However, it often leads to false indications of turbulence, since pressure and velocity fluctuations over a fluid could be well correlated in the absence of any turbulence or vorticity. Some coherent structures, such as vortex rings, etc. can be large-scale motions comparable to the extent of the shear flow. There are also coherent motions at much smaller scales such as hairpin vortices and typical eddies, which are typically known as coherent substructures, as in coherent structures which can be broken up into smaller more elementary substructures.
Characteristics
Although a coherent structure is by definition characterized by high levels of coherent vorticity, Reynolds stress, production, and heat and mass transportation, it does not necessarily require a high level of kinetic energy. In fact, one of the main roles of coherent structures is the large-scale transport of mass, heat, and momentum without requiring the high amounts of energy normally needed. Consequently, this implies that coherent structures are not the main production and cause of Reynolds stress, and incoherent turbulence can be similarly significant.
Coherent structures cannot superimpose, i.e. they cannot overlap and each coherent structure has its own independent domain and boundary. Since eddies coexist as spatial superpositions, a coherent structure is not an eddy. For example, eddies dissipate energy by obtaining energy from the mean flow at large scales, and eventually dissipating it at the smallest scales. There is no such analogous exchange of energy between coherent structures, and any interaction such as tearing between coherent structures simply results in a new structure. However, two coherent structures can interact and influence each other. The mass of a structure change with time, with the typical case being that structures increase in volume via the diffusion of vorticity.
One of the most fundamental quantities of coherent structures is characterized by coherent vorticity, . Perhaps the next most critical measures of coherent structures are the coherent vs. incoherent Reynold's stresses, and . These represent the transports of momentum, and their relative strength indicates how much momentum is being transported by coherent structures as compared to incoherent structures. The next most significant measures include contoured depictions of coherent strain rate and shear production. A useful property of such contours is that they are invariant under Galilean transformations, hence the contours of coherent vorticity constitute an excellent identifier to the structure's boundaries. The contours of these properties not only locate where exactly coherent structure quantities have their peaks and saddles, but also identify where the incoherent turbulent structures are when overlaid on their directional gradients. In addition, spatial contours can be drawn describe the shape, size, and strength of the coherent structures, depicting not only the mechanics but also the dynamical evolution of coherent structures. For example, in order for a structure to be evolving, and hence dominant, its coherent vorticity, coherent Reynolds stress, and production terms should be larger than the time averaged values of the flow structures.
Formation
Coherent structures form due to some sort of instability, e.g. the Kelvin–Helmholtz instability. Identifying an instability, and hence the initial formation of a coherent structure, requires the knowledge of initial conditions of the flow structure. Hence, documentation of the initial condition is essential for capturing the evolution and interactions of coherent structures, since initial conditions are quite variable. Overlooking the initial conditions was common in early studies due to researchers overlooking their significance. Initial conditions include the mean velocity profile, thickness, shape, the probability densities of velocity and momentum, the spectrum of Reynolds stress values, etc. These measures of initial flow conditions can be organized and grouped into three broad categories: laminar, highly disturbed, and fully turbulent.
Out of the three categories, coherent structures typically arise from instabilities in laminar or turbulent states. After an initial triggering, their growth is determined by evolutionary changes due to non-linear interactions with other coherent structures, or their decay onto incoherent turbulent structures. Observed rapid changes lead to the belief that there must be a regenerative cycle that takes place during decay. For example, after a structure decays, the result may be that the flow is now turbulent and becomes susceptible to a new instability determined by the new flow state, leading to a new coherent structure being formed. It is also possible that structures do not decay and instead distort by splitting into substructures or interacting with other coherent structures.
Categories of coherent structures
Lagrangian coherent structures
Main article: Lagrangian coherent structure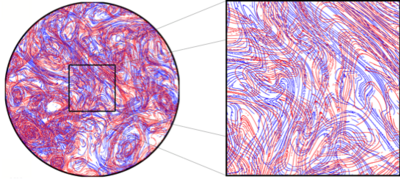
Lagrangian coherent structures (LCSs) are influential material surfaces that create clearly recognizable patterns in passive tracer distributions advected by an unsteady flow. LCSs can be classified as hyperbolic (locally maximally attracting or repelling material surfaces), elliptic (material vortex boundaries), and parabolic (material jet cores). These surfaces are generalizations of classical invariant manifolds, known in dynamical systems theory, to finite-time unsteady flow data. This Lagrangian perspective on coherence is concerned with structures formed by fluid elements, as opposed to the Eulerian notion of coherence, which considers features in the instantaneous velocity field of the fluid. Various mathematical techniques have been developed to identify LCSs in two- and three-dimenisonal data sets, and have been applied to laboratory experiments, numerical simulations and geophysical observations.
Hairpin vortices
Hairpin vortices are found on top of turbulent bulges of the turbulent wall, wrapping around the turbulent wall in hairpin shaped loops, where the name originates. The hairpin-shaped vortices are believed to be one of the most important and elementary sustained flow patterns in turbulent boundary layers. Hairpins are perhaps the simplest structures, and models that represent large scale turbulent boundary layers are often constructed by breaking down individual hairpin vortices, which could explain most of the features of wall turbulence. Although hairpin vortices form the basis of simple conceptual models of flow near a wall, actual turbulent flows may contain a hierarchy of competing vortices, each with their own degree of asymmetry and disturbances.
Hairpin vortices resemble the horseshoe vortex, which exists because of perturbations of small upward motion due to differences in upward flowing velocities depending on the distance from the wall. These form multiple packets of hairpin vortices, where hairpin packets of different sizes could generate new vortices to add to the packet. Specifically, close to the surface, the tail ends of hairpin vortices could gradually converge resulting in provoked eruptions, producing new hairpin vortices. Hence, such eruptions are a regenerative process, in which they act to create vortices near the surface and eject them out onto the outer regions of the turbulent wall. Based on the eruptive properties, such flows can be inferred to be very efficient at heat transfer because of mixing. Specifically, eruptions carry hot fluids up while cooler flows are brought downwards during the converging of tails of the hairpin vortices before erupting.
It is believed that production and contributions to , the Reynolds stress, occur during strong interactions between the inner and outer walls of hairpins. During the production of this Reynold's stress term, the contributions come in sharp intermittent time segments when eruptions bring new vortices outward.
Formation of hairpin vortices has been observed in experiments and numerical simulations of single hairpins, however observational evidence for them in nature is still limited. Theodorsen has been producing sketches that indicate the presence of hairpin vortices in his flow visualization experiments. These smaller elementary structures can be seen overlaying the main vortex in the sketch to the right (image of sketch to Theodorsen's steam experiment that exposes the presence of structures). The sketch was well advanced for the time, but with the advent of computers came better depictions. Robinson in 1952 isolated two types of flow structures that he named the "horseshoe", or arch, vortex and the "quasi-streamwise" vortex (classic figure shown to the right).

Since the mass usage of computers, direct numerical simulations or DNS have been used widely, producing vast data sets describing the complex evolution of flow. DNS indicates many complicated 3-dimensional vortices are embedded in regions of high shear near the surface. Researchers look around this region of high shear for indications of individual vortex structures based on accepted definitions, like coherent vortices. Historically, a vortex has been thought of as a region in the flow where a group of vortex lines come together hence indicating the presence of a vortex core, with groups of instantaneous circular paths about the core. In 1991, Robinson defined a vortex structure to be a core consisting of convected low pressure regions, where instantaneous streamlines can form circles or spiral shapes relative to the plane normal to the vortex core plane. Although it is not possible to track the evolution of hairpins over long periods, it is possible to identify and trace their evolution over short time periods. Some of the key notable features of hairpin vortices are how they interact with the background shear flow, other vortices, and how they interact with the flow near the surface.
References
- ^ Green, Beverley (1995-03-31). Fluid Vortices - Vol. 30 of Fluid Mechanics and Its Applications. Dordrecht: Springer Science & Business Media. ISBN 978-0-7923-3376-0.
- ^ Hussain, A. K. M. F. (1983-10-01). "Coherent structures—reality and myth". The Physics of Fluids. 26 (10). AIP Publishing: 2816–2850. doi:10.1063/1.864048. ISSN 0031-9171.
- Pope S B. Turbulent flows. 2001.
- Ganapathisubramani, B., Longmire, E. K., Marusic, I. “Characteristics of vortex packets in turbulent boundary layers” J. Fluid Mech., vol. 478, pp. 35-46 (2003).
- Mathur, M.; Haller, G.; Peacock, T.; Ruppert-Felsot, J.; Swinney, H. (2007). "Uncovering the Lagrangian Skeleton of Turbulence". Physical Review Letters. 98 (14): 144502. Bibcode:2007PhRvL..98n4502M. doi:10.1103/PhysRevLett.98.144502. PMID 17501277.
- Peacock, T., Haller, G. "Lagrangian Coherent structures: the hidden skeleton of fluid flows" Physics Today, 41 (2013). http://georgehaller.com/reprints/PhysToday.pdf
- Haller, G. (2015). "Lagrangian Coherent Structures". Annual Review of Fluid Mechanics. 47 (1): 137–162. Bibcode:2015AnRFM..47..137H. doi:10.1146/annurev-fluid-010313-141322. S2CID 122894798.
- www
.cfd-online .com /Wiki /Introduction _to _turbulence /Wall _bounded _turbulent _flows%20turbulent%20wall - Adrian, R. J. “Hairpin vortex organization in wall turbulence” Phys. Fluids 19, 041301 (2007).
- Haidari, A. H., Smith, C. R. “The generation and regeneration of single hairpin vortices” J. Fluid Mech., vol. 277, pp. 135-162. (1994)
 . Perhaps the next most critical measures of coherent structures are the coherent vs. incoherent Reynold's stresses,
. Perhaps the next most critical measures of coherent structures are the coherent vs. incoherent Reynold's stresses,  and
and  . These represent the transports of momentum, and their relative strength indicates how much momentum is being transported by coherent structures as compared to incoherent structures. The next most significant measures include contoured depictions of coherent strain rate and shear production. A useful property of such contours is that they are invariant under Galilean transformations, hence the contours of coherent vorticity constitute an excellent identifier to the structure's boundaries. The contours of these properties not only locate where exactly coherent structure quantities have their peaks and saddles, but also identify where the incoherent turbulent structures are when overlaid on their directional gradients. In addition, spatial contours can be drawn describe the shape, size, and strength of the coherent structures, depicting not only the mechanics but also the dynamical evolution of coherent structures. For example, in order for a structure to be evolving, and hence dominant, its coherent vorticity, coherent Reynolds stress, and production terms should be larger than the time averaged values of the flow structures.
. These represent the transports of momentum, and their relative strength indicates how much momentum is being transported by coherent structures as compared to incoherent structures. The next most significant measures include contoured depictions of coherent strain rate and shear production. A useful property of such contours is that they are invariant under Galilean transformations, hence the contours of coherent vorticity constitute an excellent identifier to the structure's boundaries. The contours of these properties not only locate where exactly coherent structure quantities have their peaks and saddles, but also identify where the incoherent turbulent structures are when overlaid on their directional gradients. In addition, spatial contours can be drawn describe the shape, size, and strength of the coherent structures, depicting not only the mechanics but also the dynamical evolution of coherent structures. For example, in order for a structure to be evolving, and hence dominant, its coherent vorticity, coherent Reynolds stress, and production terms should be larger than the time averaged values of the flow structures.
 , the Reynolds stress, occur during strong interactions between the inner and outer walls of hairpins. During the production of this Reynold's stress term, the contributions come in sharp intermittent time segments when eruptions bring new vortices outward.
, the Reynolds stress, occur during strong interactions between the inner and outer walls of hairpins. During the production of this Reynold's stress term, the contributions come in sharp intermittent time segments when eruptions bring new vortices outward.