Col is a pencil and paper game, specifically a map-coloring game, involving the shading of areas in a line drawing according to the rules of graph coloring. With each move, the graph must remain proper (no two areas of the same colour may touch), and a player who cannot make a legal move loses. The game was described and analysed by John Conway, who attributed it to Colin Vout, in On Numbers and Games.
Example game
In the following game, the first of the two players is using red, and the second is using blue. The last move in each image is shown brighter than the other areas.
The starting graph:
The first player may colour any of the areas to begin. However, the region around the outside of the graph is not included as an area for this game.
After the first move:
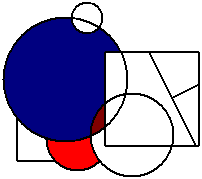
The second player now colours a white cell. As no areas are currently blue, any white cell is allowed.
Two moves in:
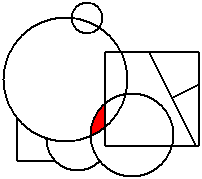
At this point, the requirement that the graph be proper comes into effect, as a red area must be made which does not touch the existing one:
Once the third region is coloured:
Note that areas only count as touching if they share edges, not if they only share vertices, so this move is legal.
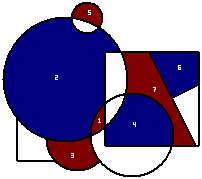
The game continues, players moving alternately, until one player cannot make a move. This player loses. A possible continuation of the game is as follows (with each move numbered for clarity):
Game over:
In this outcome, the blue player has lost.
Snort
Snort, invented by Simon P. Norton, uses a similar partisan assignment of two colors, but with the anticlassical constraint: neighboring regions are not allowed to be given different colors. Coloring the regions is explained as assigning fields to bulls and cows, where neighboring fields may not contain cattle of the opposite sex, lest they be distracted from their grazing.
Deciding the outcome in Snort is PSPACE-complete on general graphs. This is proven by reducing partizan node Kayles, which is PSPACE-complete, to a game of Snort.
Analysis
The value of a Col position is always either a number or a number plus star This makes the game relatively simple compared with Snort, which features a much greater variety of values.
References
- Berlekamp, Elwyn R.; John H. Conway; Richard K. Guy (1982). Winning Ways for your Mathematical Plays. Academic Press. ISBN 978-0-12-091101-1. Revised and reprinted as
- Berlekamp, Elwyn R. (2004) . Winning Ways for your Mathematical Plays (2nd ed.). A K Peters Ltd. ISBN 978-1-56881-130-7.
- Conway, John Horton (1976). On numbers and games. Academic Press. ISBN 978-0-12-186350-0. Revised and reprinted as
- Conway, John Horton (2000). On numbers and games. A K Peters Ltd. ISBN 978-1-56881-127-7.
- On Numbers and Games: 1
- Demaine, Erik; Hearn, Robert (2001). "Playing Games with Algorithms: Algorithmic Combinatorial Game Theory". arXiv:cs/0106019v2.
- Winning Ways: 2